このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
predictorImportance
分類木の予測子の重要度の推定
説明
例
フィッシャーのアヤメのデータ セットを読み込みます。
load fisheriris分類木を成長させます。
Mdl = fitctree(meas,species);
すべての予測子変数について予測子の重要度の推定を計算します。
imp = predictorImportance(Mdl)
imp = 1×4
0 0 0.0907 0.0682
imp の最初の 2 つの要素はゼロです。そのため、最初の 2 つの予測子は、アヤメを分類するための Mdl の計算には入りません。
予測子の重要度の推定は、代理分岐を使用する場合、予測子の順序には依存しませんが、代理分岐を使用しない場合には、予測子の順序に依存します。
前の例のデータ列の順序を並べ替え、別の分類木を成長させてから、予測子の重要度の推定を計算します。
measPerm = meas(:,[4 1 3 2]); MdlPerm = fitctree(measPerm,species); impPerm = predictorImportance(MdlPerm)
impPerm = 1×4
0.1515 0 0.0074 0
予測子の重要度の推定は imp の並べ替えにはなりません。
フィッシャーのアヤメのデータ セットを読み込みます。
load fisheriris分類木を成長させます。代理分岐を使用するよう指定します。
Mdl = fitctree(meas,species,'Surrogate','on');
すべての予測子変数について予測子の重要度の推定を計算します。
imp = predictorImportance(Mdl)
imp = 1×4
0.0791 0.0374 0.1530 0.1529
すべての予測子にいくらかの重要度があります。最初の 2 つの予測子は最後の 2 つよりも重要度が低くなっています。
前の例のデータ列の順序を並べ替え、代理分岐を使用するよう指定して別の分類木を成長させてから、予測子の重要度の推定を計算します。
measPerm = meas(:,[4 1 3 2]); MdlPerm = fitctree(measPerm,species,'Surrogate','on'); impPerm = predictorImportance(MdlPerm)
impPerm = 1×4
0.1529 0.0791 0.1530 0.0374
予測子の重要度の推定は imp の並べ替えになります。
census1994 データ セットを読み込みます。年齢、労働階級、教育レベル、婚姻区分、人種、性別、資本利得および損失、および 1 週間の勤務時間が与えられた個人の給与カテゴリを予測するモデルを考えます。
load census1994 X = adultdata(:,{'age','workClass','education_num','marital_status','race',... 'sex','capital_gain','capital_loss','hours_per_week','salary'});
summary を使用して、カテゴリカル変数で表現されるカテゴリの個数を表示します。
summary(X)
X: 32561×10 table
Variables:
age: double
workClass: categorical (8 categories)
education_num: double
marital_status: categorical (7 categories)
race: categorical (5 categories)
sex: categorical (2 categories)
capital_gain: double
capital_loss: double
hours_per_week: double
salary: categorical (2 categories)
Statistics for applicable variables:
NumMissing Min Median Max Mean Std
age 0 17 37 90 38.5816 13.6404
workClass 1836
education_num 0 1 10 16 10.0807 2.5727
marital_status 0
race 0
sex 0
capital_gain 0 0 0 99999 1.0776e+03 7.3853e+03
capital_loss 0 0 0 4356 87.3038 402.9602
hours_per_week 0 1 40 99 40.4375 12.3474
salary 0
カテゴリカル変数で表現されるカテゴリの数は連続変数のレベル数と比較するとわずかなので、予測子分割アルゴリズムの標準 CART ではカテゴリカル変数よりも連続予測子が分割されます。
データ セット全体を使用して分類木に学習をさせます。偏りの無い木を成長させるため、予測子の分割に曲率検定を使用するよう指定します。データには欠損観測値が含まれているので、代理分岐を使用するよう指定します。
Mdl = fitctree(X,'salary','PredictorSelection','curvature',... 'Surrogate','on');
すべての予測子について分割によるリスク変動を合計し、この合計を枝ノード数で除算することにより、予測子の重要度の値を推定します。棒グラフを使用して推定を比較します。
imp = predictorImportance(Mdl); figure; bar(imp); title('Predictor Importance Estimates'); ylabel('Estimates'); xlabel('Predictors'); h = gca; h.XTickLabel = Mdl.PredictorNames; h.XTickLabelRotation = 45; h.TickLabelInterpreter = 'none';
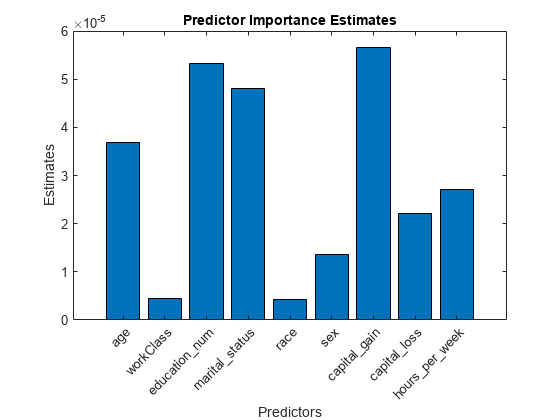
このケースでは、最も重要な予測子は capital_gain であり、次に重要なのは education_num です。
入力引数
詳細
拡張機能
バージョン履歴
R2011a で導入
