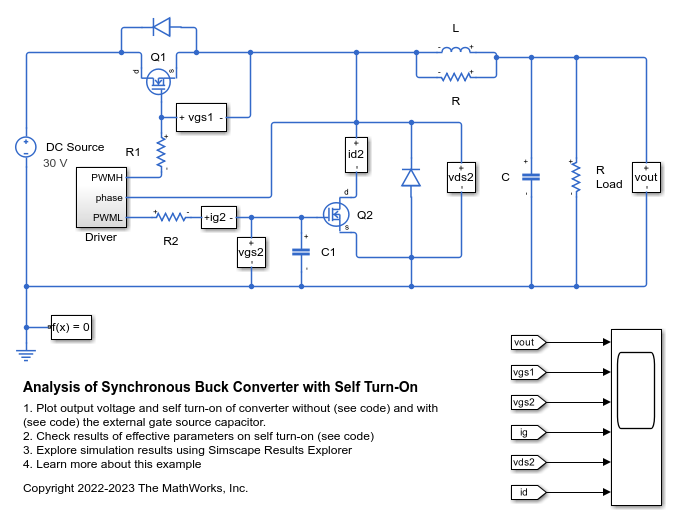
N-Channel MOSFET

N-Channel metal-oxide-semiconductor field-effect transistor using either Shichman-Hodges equation or surface-potential-based model

expand all in page

Libraries:
Simscape / Electrical / Semiconductors & Converters

Description

The N-Channel MOSFET block provides two main modeling options:

Based on threshold voltage — Uses the Shichman-Hodges equation to represent the device. This modeling approach, based on threshold voltage, has the benefits of simple parameterization and simple current-voltage expressions. However, these models have difficulty in accurately capturing transitions across the threshold voltage and lack some important effects, such as velocity saturation. For details, see Threshold-Based Model.
This modeling option provides four ways of parameterizing an N-Channel MOSFET:
- By specifying parameters from a datasheet.
- By specifying equation parameters directly.
- By a 2-D lookup table approximation to the I-V (current-voltage) curve. For details, see Representation by 2-D Lookup Table.
- By a 3-D lookup table approximation to the I-V (current-voltage) curve that includes temperature data. For details, see Representation by 3-D Lookup Table.
Based on surface potential — Uses the surface-potential equation to represent the device. This modeling approach provides a greater level of model fidelity than the simple square-law (threshold-voltage-based) models can provide. The trade-off is that there are more parameters that require extraction. For details, see Surface-Potential-Based Model.

Together with the thermal port options (see Thermal Port), the block therefore provides you with four choices. To select the desired option, set the Modeling option parameter to either:

Threshold-based — Basic model, which represents the device using the Shichman-Hodges equation (based on threshold voltage) and does not simulate thermal effects. This is the default.
Threshold-based with thermal — Model based on threshold voltage and with exposed thermal port.
Surface-potential-based — Model based on surface potential. This model does not simulate thermal effects.
Surface-potential-based with thermal — Thermal modeling option of the model based on surface potential.

Threshold-Based Model

The threshold-based option of the block uses the Shichman and Hodges equations [1] for an insulated-gate field-effect transistor to represent an N-Channel MOSFET.

The drain-source current, I_DS, depends on the region of operation:

In the off region (V_GS < V_th), the drain-source current is:

$I_{D S} = 0$
In the linear region (0 < V_DS < V_GS –V_th), the drain-source current is:

$I_{D S} = K ((V_{G S} - V_{t h}) V_{D S} - V_{D S}^{2} / 2) (1 + λ | V_{D S} |)$
In the saturated region (0 < V_GS –V_th < V_DS), the drain-source current is:

$I_{D S} = (K / 2) {(V_{G S} - V_{t h})}^{2} (1 + λ | V_{D S} |)$

In the preceding equations:

K is the transistor gain.
V_DS is the positive drain-source voltage.
V_GS is the gate-source voltage.
V_th is the threshold voltage. For the four terminal parameterization, V_th is obtained using these equations:

V_BS Range V_th Equation
$V_{B S} \leq 0$ $V_{t h} = V_{T 0} + γ (- \sqrt{2 ϕ_{B}}) + γ (\sqrt{2 ϕ_{B} - V_{B S}})$
$0 < V_{B S} \leq 4 ϕ_{B}$ $V_{t h} = V_{T 0} - \frac{γ V_{B S}}{\sqrt{2 ϕ_{B}}}$
$V_{B S} > 4 ϕ_{B}$ $V_{t h} = V_{T 0} + γ (- \sqrt{2 ϕ_{B}})$
λ is the channel modulation.

V_BS Range	V_th Equation
$V_{B S} \leq 0$	$V_{t h} = V_{T 0} + γ (- \sqrt{2 ϕ_{B}}) + γ (\sqrt{2 ϕ_{B} - V_{B S}})$
$0 < V_{B S} \leq 4 ϕ_{B}$	$V_{t h} = V_{T 0} - \frac{γ V_{B S}}{\sqrt{2 ϕ_{B}}}$
$V_{B S} > 4 ϕ_{B}$	$V_{t h} = V_{T 0} + γ (- \sqrt{2 ϕ_{B}})$

To specify the parallel conductance of the channel, connect an Environment Parameters block to the electrical network. Then, set the minimum conductance of the N-Channel MOSFET block and other SPICE-compatible blocks by setting the GMIN parameter of the Environment Parameters block.

Charge Model for Threshold-Based Modeling Option

The block models capacitances either by fixed capacitance values, or by tabulated values as a function of the drain-source voltage. In either case, you can either directly specify the gate-source and gate-drain capacitance values, or let the block derive them from the input and reverse transfer capacitance values. Therefore, the Parameterization options for charge model on the Capacitance setting are:

Specify fixed input, reverse transfer and output capacitance — Provide fixed parameter values from datasheet and let the block convert the input and reverse transfer capacitance values to capacitance values, as described below. This is the default method.
Specify fixed gate-source, gate-drain and drain-source capacitance — Provide fixed values for capacitance parameters directly.
Specify tabulated input, reverse transfer and output capacitance — Provide tabulated capacitance and drain-source voltage values based on datasheet plots. The block converts the input and reverse transfer capacitance values to capacitance values, as described below.
Specify tabulated gate-source, gate-drain and drain-source capacitance — Provide tabulated values for capacitances and drain-source voltage.

Use one of the tabulated capacitance options (Specify tabulated input, reverse transfer and output capacitance or Specify tabulated gate-source, gate-drain and drain-source capacitance) when the datasheet provides a plot of capacitances as a function of drain-source voltage. Using tabulated capacitance values gives more accurate dynamic characteristics and avoids the need for interactive tuning of parameters to fit the dynamics.

If you use the Specify fixed gate-source, gate-drain and drain-source capacitance or Specify tabulated gate-source, gate-drain and drain-source capacitance option, the Capacitance setting lets you specify the Gate-drain capacitance, Cgd, Gate-source capacitance, Cgs, and Drain-source capacitance, Cds parameter values (fixed or tabulated) directly. Otherwise, the block derives them from the Input capacitance, Ciss, Reverse transfer capacitance, Crss, and Output capacitance, Coss parameter values. These two parameterization methods are related as follows:

C_GD = Crss
C_GS = Ciss – Crss
C_DS = Coss – Crss

For the four terminals parameterization, the Input capacitance, Ciss, Reverse transfer capacitance, Crss, and Output capacitance, Coss are obtained using these equations:

C_GD = Crss
C_GS + C_GB = Ciss – Crss
C_DB = Coss – Crss

A simplified Meyer's capacitance model describes the gate-source capacitance, C_GS, the gate-bulk capacitance, C_GB, and the gate-drain capacitance, C_GD.

This figure shows how C_GB and C_GS change, when the gate-source voltage V_gs reaches the threshold voltage V_th, if you set the Gate-bulk and gate-source charge-voltage linearity parameter to Gate-bulk and gate-source capacitance change instantly.

This figure shows how C_GB and C_GS change, when V_gs is between V_th –2Φ_B and V_th, if you set the Gate-bulk and gate-source charge-voltage linearity parameter to Gate-bulk and gate-source capacitance change gradually.

The two fixed capacitance options (Specify fixed input, reverse transfer and output capacitance or Specify fixed gate-source, gate-drain and drain-source capacitance) let you model gate capacitance as a fixed gate-source capacitance C_GS and either a fixed or a nonlinear gate-drain capacitance C_GD. If you select the Gate-drain charge function is nonlinear option for the Gate-drain charge-voltage linearity parameter, then the gate-drain charge relationship is defined by the piecewise-linear function shown in the following figure.

For instructions on how to map a time response to device capacitance values, see the N-Channel IGBT block reference page. However, this mapping is only approximate because the Miller voltage typically varies more from the threshold voltage than in the case for the IGBT.

Note

Because this block implementation includes a charge model, you must model the impedance of the circuit driving the gate to obtain representative turn-on and turn-off dynamics. Therefore, if you are simplifying the gate drive circuit by representing it as a controlled voltage source, you must include a suitable series resistor between the voltage source and the gate.

Representation by 2-D Lookup Table

For the lookup table representation of the detailed block modeling option, you provide tabulated values for drain-source currents as a function of gate-source voltage and drain-source voltage. The main advantage of using this option is simulation speed. It also lets you parameterize the device from either measured data or from data obtained from another simulation environment.

This figure shows the implementation of the 2-D lookup table option when you set Ids-Vds parameterization to Provide negative and positive Vds data:

This figure shows the implementation of the 2-D lookup table option when you set Ids-Vds parameterization to Provide positive Vds data only:

For the four terminal MOSFET, the surface potential and body factor values are calculated based on the nearest threshold voltage as shown in this picture:

Note

To ensure that the signs of the drain-source current and drain-source voltage are consistent:

If the drain-source voltage is equal to 0, the value of the Tabulated drain-source currents, Ids(Vgs,Vds) parameter must be equal to 0.
The tabulated power, which is the product of the Tabulated drain-source currents, Ids(Vgs,Vds) parameter and the drain-source voltage, must be greater than or equal to 0.
The tabulated conductance, which is the gradient of the Tabulated drain-source currents, Ids(Vgs,Vds) parameter with respect to the drain-source voltage V_ds, must be greater than or equal to 0.
The first gradient of the Tabulated drain-source currents, Ids(Vgs,Vds) parameter, with respect to gate-source voltage V_gs, must be equal to 0.

Representation by 3-D Lookup Table

For the temperature-dependent lookup table representation of the detailed block modeling option, you provide tabulated values for drain-source currents as a function of gate-source voltage, drain-source voltage, and temperature.

Note

To ensure that the signs of the drain-source current and drain-source voltage are consistent:

If the drain-source voltage is equal to 0, the value of the Tabulated drain-source currents, Ids(Vgs,Vds,T) parameter must be equal to 0.
The tabulated power, which is the product of the Tabulated drain-source currents, Ids(Vgs,Vds,T) parameter and the drain-source voltage, must be greater than or equal to 0.
The tabulated conductance, which is the gradient of the Tabulated drain-source currents, Ids(Vgs,Vds,T) parameter with respect to the drain-source voltage V_ds, must be greater than or equal to 0.
The first gradient of the Tabulated drain-source currents, Ids(Vgs,Vds,T) parameter, with respect to gate-source voltage V_gs, must be equal to 0.

Surface-Potential-Based Model

The surface-potential-based modeling option of the block provides a greater level of model fidelity than the simple square-law (threshold-voltage-based) model. The surface-potential-based block modeling option includes the following effects:

Fully nonlinear capacitance model (including the nonlinear Miller capacitance)
Charge conservation inside the model, so you can use the model for charge sensitive simulations
Velocity saturation and channel-length modulation
The intrinsic body diode
Reverse recovery in the body diode model
Temperature scaling of physical parameters
For the thermal modeling option, dynamic self-heating (that is, you can simulate the effect of self-heating on the electrical characteristics of the device)

This model is a minimal version of the world-standard PSP model (see https://briefs.techconnect.org/papers/introduction-to-psp-mosfet-model/), including only certain effects from the PSP model in order to strike a balance between model fidelity and complexity. For details of the physical background to the phenomena included in this model, see [2].

The basis of the model is Poisson equation:

$\frac{\partial^{2} ψ}{\partial x^{2}} + \frac{\partial^{2} ψ}{\partial y^{2}} = \frac{q N_{A}}{ε_{S i}} [1 - \exp (\frac{- ψ}{ϕ_{T}}) + \exp (\frac{ψ - 2 ϕ_{B} - V_{C B}}{ϕ_{T}})]$

$ϕ_{T} = \frac{k_{B} T}{q}$

where:

ψ is the electrostatic potential.
q is the magnitude of the electronic charge.
N_A is the density of acceptors in the substrate.
ɛ_Si is the dielectric permittivity of the semiconductor material (for example, silicon).
ϕ_B is the difference between the intrinsic Fermi level and the Fermi level in the bulk silicon.
V_CB is the quasi-Fermi potential of the surface layer referenced to the bulk.
ϕ_T is the thermal voltage.
k_B is Boltzmann’s constant.
T is temperature.

Poisson equation is used to derive the surface-potential equation:

${(V_{G B} - V_{F B} - ψ_{s})}^{2} = γ^{2} [ψ_{s} + ϕ_{T} (\exp (\frac{- ψ_{s}}{ϕ_{T}}) - 1) + ϕ_{T} \exp (- \frac{2 ϕ_{B} + V_{C B}}{ϕ_{T}}) (\exp (\frac{ψ_{s}}{ϕ_{T}}) - 1)]$

where:

V_GB is the applied gate-body voltage.
V_FB is the flatband voltage.
ψ_s is the surface potential.
γ is the body factor,

$γ = \frac{\sqrt{2 q ε_{S i} N_{A}}}{C_{o x}}$

C_ox is the capacitance per unit area.

The block uses an explicit approximation to the surface-potential equation, to avoid the need for numerical solution to this implicit equation.

Once the surface potential is known, the drain current I_D is given by

$I_{D} = \frac{W μ_{0}}{L G_{Δ L} G_{m o b} \sqrt{1 + {(θ_{s a t} Δ ψ)}^{2}}} [- {\bar{Q}}_{i n v} Δ ψ + ϕ_{T} (Q_{i n v L} - Q_{i n v 0})]$

where:

W is the device width.
L is the channel length.
μ₀ is the low-field mobility.
θ_sat is the velocity saturation.
Δψ is the difference in the surface potential between the drain and the source.
Q_inv0 and Q_invL are the inversion charge densities at the source and drain, respectively.
${\bar{Q}}_{i n v}$ is the average inversion charge density across the channel.
G_mob is the mobility reduction factor. For more information, see the Surface roughness scattering factor parameter description in the Main (Surface-Potential-Based Modeling Option) section.
G_ΔL is the channel-length modulation.

$G_{Δ L} = 1 - \frac{Δ L}{L} = 1 - α \ln [\frac{V_{D B} - V_{D B, e f f} + \sqrt{{(V_{D B} - V_{D B, e f f})}^{2} + V_{p}^{2}}}{V_{p}}]$

where:

α is the channel-length modulation factor.
V_DB is the drain-body voltage.
V_DB,eff is the drain-body voltage clipped to a maximum value corresponding to velocity saturation or pinch-off (whichever occurs first).
V_p is the channel-length modulation voltage.

The block computes the inversion charge densities directly from the surface potential.

The block also computes the nonlinear capacitances from the surface potential. Source and drain charge contributions are assigned via a bias-dependent Ward-Dutton charge-partitioning scheme, as described in [3]. These charges are computed explicitly, so this model is charge-conserving. The capacitive currents are computed by taking the time derivatives of the relevant charges. In practice, the charges within the simulation are normalized to the oxide capacitance and computed in units of volts.

The MOSFET gain, β, is given by

$β = \frac{W μ_{0} C_{o x}}{L}$

The threshold voltage for a short-circuited source-bulk connection is approximately given by

$V_{T} = V_{F B} + 2 ϕ_{B} + 2 ϕ_{T} + γ \sqrt{2 ϕ_{B} + 2 ϕ_{T}}$

where:

2ϕ_B is the surface potential at strong inversion.

The overall three and four terminal models consist of an intrinsic MOSFET defined by the surface-potential formulation, a body diode, series resistances, and fixed overlap capacitances, as shown in the schematics.

Modeling Body Diode

The block models the body diode either as an ideal, exponential diode or as a tabulated diode.

Exponential Diode

When you set Model body diode to Exponential, the junction and diffusion capacitances are:

$I_{d i o} = I_{s} [\exp (- \frac{V_{D B}}{n ϕ_{T}}) - 1]$

$C_{j} = \frac{C_{j 0}}{\sqrt{1 + \frac{V_{D B}}{V_{b i}}}}$

$C_{d i f f} = \frac{τ I_{s}}{n ϕ_{T}} \exp (- \frac{V_{D B}}{n ϕ_{T}})$

where:

I_dio is the current through the diode.
I_s is the reverse saturation current.
V_DB is the drain-body voltage.
n is the ideality factor.
ϕ_T is the thermal voltage.
C_j is the junction capacitance of the diode.
C_j0 is the zero-bias junction capacitance.
V_bi is the built-in voltage.
C_diff is the diffusion capacitance of the diode.
τ is the transit time.

The capacitances are defined through an explicit calculation of charges, which are then differentiated to give the capacitive expressions above. The block computes the capacitive diode currents as time derivatives of the relevant charges, similar to the computation in the surface-potential-based MOSFET model.

Tabulated Diode

To model a tabulated diode, set the Model body diode parameter to Tabulated I-V curve. This figure shows the implementation of the tabulated diode option:

When choosing this parameterization, you must provide the data for the forward bias only.

The block implements the diode using a smooth interpolation option. If the diode exceeds the provided tabulated data range, the block uses a linear extrapolation technique at the last voltage-current data point.

To specify the off conductance of the tabulated diode, set the Diode off conductance parameter. (since R2024a)

Note

The tabulated diode does not model the reverse breakdown.

Modeling Temperature Dependence

The default behavior is that dependence on temperature is not modeled, and the device is simulated at the temperature for which you provide block parameters. To model the dependence on temperature during simulation, select Model temperature dependence for the Parameterization parameter in the Temperature Dependence setting.

Threshold-Based Model

For threshold-based modeling option, you can include modeling the dependence of the transistor static behavior on temperature during simulation. Temperature dependence of the capacitances is not modeled, this being a much smaller effect.

When including temperature dependence, the transistor defining equations remain the same. The gain, K, and the threshold voltage, V_th, become a function of temperature according to the following equations:

$K_{T s} = K_{T m 1} {(\frac{T_{s}}{T_{m 1}})}^{B E X}$

V_ths = V_th1 + α (T_s – T_m1)

where:

T_m1 is the temperature at which the transistor parameters are specified, as defined by the Measurement temperature parameter value.
T_s is the simulation temperature.
K_Tm1 is the transistor gain at the measurement temperature.
K_Ts is the transistor gain at the simulation temperature. This is the transistor gain value used in the MOSFET equations when temperature dependence is modeled.
V_th1 is the threshold voltage at the measurement temperature.
V_ths is the threshold voltage at the simulation temperature. This is the threshold voltage value used in the MOSFET equations when temperature dependence is modeled.
BEX is the mobility temperature exponent. A typical value of BEX is -1.5.
α is the gate threshold voltage temperature coefficient, dV_th/dT.

For the four terminals parameterization, V_th is obtained using these equations:

V_BS Range	V_th Equation
$V_{B S} \leq 0$	$\frac{d V_{t h}}{d T} = \frac{d V_{T 0}}{d T} - \frac{γ}{2 \sqrt{2 ϕ_{B}}} \frac{d 2 ϕ_{B}}{d T} + \frac{γ}{2 \sqrt{2 ϕ_{B} - V_{B S}}} \frac{d 2 ϕ_{B}}{d T}$
$0 < V_{B S} \leq 4 ϕ_{B}$	$\frac{d V_{t h}}{d T} = \frac{d V_{T 0}}{d T} - \frac{γ V_{B S}}{4} {(2 ϕ_{B})}^{- \frac{3}{2}} \frac{d 2 ϕ_{B}}{d T}$
$V_{B S} > 4 ϕ_{B}$	$\frac{d V_{t h}}{d T} = \frac{d V_{T 0}}{d T} - \frac{γ}{2 \sqrt{2 ϕ_{B}}} \frac{d 2 ϕ_{B}}{d T}$

Where:

$ϕ_{B} = \frac{k T}{q} \ln (\frac{N_{B}}{n_{i}})$ is the surface potential and $\frac{d 2 ϕ_{B}}{d T} = \frac{1}{T} [2 ϕ_{B} - (\frac{E_{g} (0)}{q} + \frac{3 k T}{q})]$ .
E_g(0) is the extrapolated zero degree band-gap, which is equal to 1.16 eV for silicon.
V_BS is the bulk-source voltage.

For most MOSFETS, you can use the default value of -1.5 for BEX. Some datasheets quote the value for α, but most typically they provide the temperature dependence for drain-source on resistance, R_DS(on). Depending on the block parameterization method, you have two ways of specifying α:

If you parameterize the block from a datasheet, you have to provide R_DS(on) at a second measurement temperature. The block then calculates the value for α based on this data.
If you parameterize by specifying equation parameters, you have to provide the value for α directly.

If you have more data comprising drain current as a function of gate-source voltage for more than one temperature, then you can also use Simulink^® Design Optimization™ software to help tune the values for α and BEX.

Surface-Potential-Based Model

The surface-potential-based model includes temperature effects on the capacitance characteristics, as well as modeling the dependence of the transistor static behavior on temperature during simulation.

The Measurement temperature parameter on the Main setting specifies temperature T_m1 at which the other device parameters have been extracted. The Temperature Dependence setting provides the simulation temperature, T_s, and the temperature-scaling coefficients for the other device parameters. For more information, see Temperature Dependence (Surface-Potential-Based Modeling Option).

Faults

To model a fault in the N-Channel MOSFET block, in the Faults section, click the Add fault hyperlink next to the fault that you want to model. In the Add Fault window, specify the fault properties. For more information about fault modeling, see Fault Behavior Modeling and Fault Triggering.

The N-Channel MOSFET block models five types of fault:

Open circuit — Failure due to metallization burnout
Drain-source short — Failure due to avalanche breakdown on drain-source channel
Drain-bulk short or source-bulk short — Failure due to avalanche breakdown on drain-bulk or source-bulk channels
Gate oxide short — Failure of the gate oxide dielectric layer
Parameter shift — Failure due to aging

The block can trigger fault events at a specific time or when the current or voltage exceed the limit for longer than a specific time interval.

Parameter Shift Fault

If, in the Faults settings, you set the Failure mode parameter to Parameter shift, the MOSFET fails due to the aging of its components. This equation defines the value of the shifted parameters:

$P a r a m e t e r (t) = P a r a m e t e r_{f a u l t e d} - (P a r a m e t e r_{f a u l t e d} - P a r a m e t e r_{u n f a u l t e d}) sech (\frac{t - t_{t h}}{τ}),$

where t_th is the time threshold when the fault is triggered and τ is the value of the Fault transition time constant, tau parameter.

Gate Oxide Short Fault

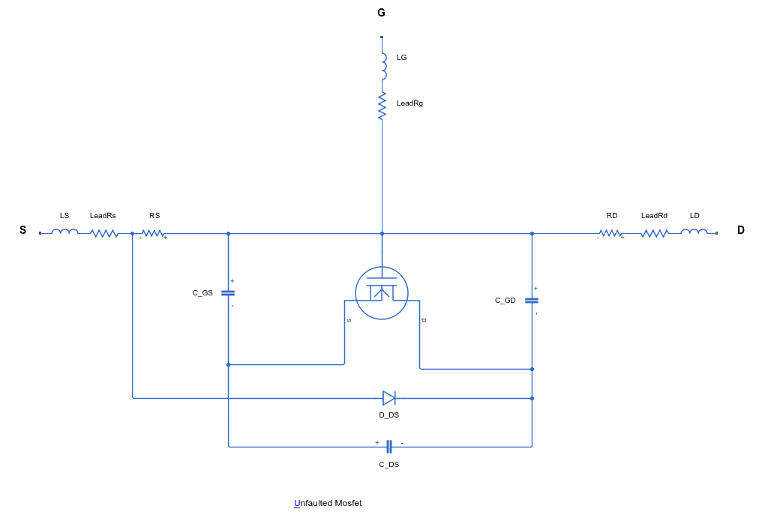
If, in the Faults settings, you set the Failure mode parameter to Gate oxide short, the gate oxide dielectric layer fails. These figures show the equivalent circuits for the three-terminal MOSFET in the unfaulted and faulted state:

These figures show the equivalent circuits for the four-terminal MOSFET in the unfaulted and faulted state:

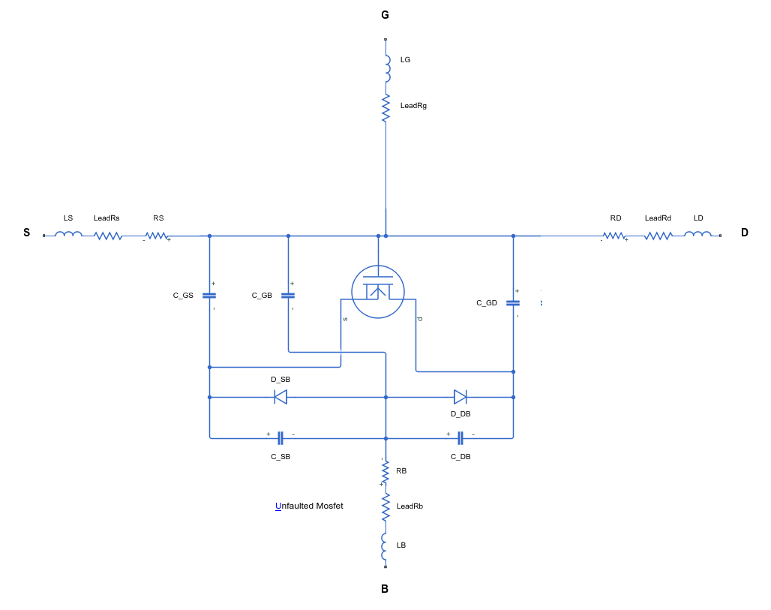
Thermal Port

The block has an optional thermal port, hidden by default. To expose the thermal port, set the Modeling option parameter to:

Threshold-based with thermal — Model based on threshold voltage and with exposed thermal port
Surface-potential-based with thermal — Model based on surface potential and with exposed thermal port

This action displays the thermal port H on the block icon, and exposes the Thermal Port parameters.

Use the thermal port to simulate the effects of generated heat and device temperature. For more information on using thermal ports and on the Thermal Port parameters, see Simulating Thermal Effects in Semiconductors.

Variables

To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Use nominal values to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. Nominal values can come from different sources. One of these sources is the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.

This table shows the relationship between the capacitances of the block and the initial targets:

Defined Capacitance	Initial Targets
Gate-emitter capacitance, Cge	Set the initial target for the gate-emitter capacitance voltage only. Set the initial target of the collector-emitter capacitance voltage to `0` or set its priority to `None`.
Collector-emitter capacitance, Cce	Set the initial target for the collector-emitter capacitance voltage only. Set the initial target of the gate-emitter capacitance voltage to `0` or set its priority to `None`.
Gate-collector capacitance, Cgc	Set the initial targets for the gate-collector voltages by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and collector-emitter.
Gate-emitter capacitance, Cge, and gate-collector capacitance, Cgc	Set the initial targets for the gate-emitter and gate-collector voltages by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and the collector-emitter.
Gate-emitter capacitance, Cge, and collector-emitter capacitance, Cce	Set the initial target for the gate-emitter and the collector-emitter capacitance.
Gate-collector capacitance, Cgc, and collector-emitter capacitance, Cce	Set the initial targets for the gate-collector and collector-emitter voltages by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and the collector-emitter.
Gate-emitter capacitance, Cge, gate-collector capacitance, Cgc, and collector-emitter capacitance, Cce	Set the initial targets for the gate-emitter, gate collector and collector-emitter capacitances by applying constraints on the gate-emitter and collector-emitter voltages. The initial condition of the gate-collector capacitance voltage is equal to the voltage between the gate-emitter and the collector-emitter.

Note

Inside your model, the number of initial targets with Priority equal to Low or High must match the number of differential variables. The differential variables come from the inductors and the capacitances in the model.

Plot Device Characteristics

You can plot the basic I-V characteristics of the N-Channel MOSFET block without building a complete model. Use the plots to explore the impact of your parameter choices on device characteristics. If you parameterize the block from a datasheet, you can compare your plots to the datasheet to check that you parameterized the block correctly. If you have a complete working model but do not know which manufactured part to use, you can compare your plots to datasheets to help you decide.

To enable this option, set the Modeling option parameter of the N-Channel MOSFET block to Threshold Based or Surface potential based. To plot the basic characteristics, right-click the block and select Electrical > Basic characteristics from the context menu. For more information about the Basic characteristics option, see Plot Basic I-V Characteristics of Semiconductor Blocks.

The N-Channel MOSFET blocks also supports the Explore characteristics option. Use this option to perform an in-depth study of block characteristics and match the block behavior to a set of target characteristics. To enable this option, set the Modeling option parameter of the block to Surface potential based. Then, right-click the block and select Electrical > Explore characteristics from the context menu. For more information about this option, see MOSFET Characteristics Viewer.

Examples

MOSFET Characteristics

Generation of the characteristic curves for an N-channel MOSFET. Define the vector of gate voltages and minimum and maximum drain-source voltages by double clicking on the block labeled 'Define Conditions (Vg and Vds)'. Then click on hyperlink plot results in the model.

Open Model

Interactive Generation of MOSFET Characteristics

Explore the impact of parameter choices on the I-V and C-V characteristics for a surface-potential-based MOSFET model. To open the MOSFET Characteristics window, in the MATLAB® Command Window, type MOSFETParameterAnalyzer.

Open Model

Analysis of Synchronous Buck Converter with Self Turn-On

How the MOSFET parameters affect the self turn-on mechanism and how you can prevent it.

Open Model

Assumptions and Limitations

When modeling temperature dependence for the threshold-based block modeling option, consider the following:

The block does not account for temperature-dependent effects on the capacitances.
When you specify R_DS(on) at a second measurement temperature, it must be quoted for the same working point (that is, the same drain current and gate-source voltage) as for the other R_DS(on) value. Inconsistent values for R_DS(on) at the higher temperature will result in unphysical values for α and unrepresentative simulation results. Typically R_DS(on) increases by a factor of about 1.5 for a hundred degree increase in temperature.
You may need to tune the values of BEX and threshold voltage, V_th, to replicate the I_DS–V_GS relationship (if available) for a given device. Increasing V_th moves the I_DS-–V_GS plots to the right. The value of BEX affects whether the I_DS–V_GS curves for different temperatures cross each other, or not, for the ranges of V_DS and V_GS considered. Therefore, an inappropriate value can result in the different temperature curves appearing to be reordered. Quoting R_DS(on) values for higher currents, preferably close to the current at which it will operate in your circuit, will reduce sensitivity to the precise value of BEX.

Ports

Conserving

expand all

G — Gate terminal
electrical

Electrical conserving port associated with the transistor gate terminal.

D — Drain terminal
electrical

Electrical conserving port associated with the transistor drain terminal.

S — Source terminal
electrical

Electrical conserving port associated with the transistor source terminal.

B — Body terminal
electrical

Electrical conserving port associated with the transistor body terminal.

Dependencies

To enable this port, set Parameterization to Four.

H — Thermal port
thermal

Thermal conserving port.

Dependencies

To enable this port, set Modeling option to Threshold-based with thermal or Surface-potential-based with thermal.

Parameters

expand all

Modeling Option — MOSFET representation
`Threshold-based` (default) | `Threshold-based with thermal` | `Surface-potential-based` | `Surface-potential-based with thermal`

Select the MOSFET representation:

Threshold-based — Basic model, which represents the device using the Shichman-Hodges equation (based on threshold voltage) and does not simulate thermal effects. This is the default.
Threshold-based with thermal — Model based on threshold voltage and with exposed thermal port.
Surface-potential-based — Model based on surface potential. This model does not simulate thermal effects.
Surface-potential-based with thermal — Thermal modeling option of the model based on surface potential.

Main (Threshold-Based Modeling Option)

This configuration of the Main parameters corresponds to the threshold-based block modeling option, which is the default. If you are using the surface-potential-based modeling option of the block, see Main (Surface-Potential-Based Modeling Option).

Number of terminals — Terminal parameterization
`Three` (default) | `Four`

Number of terminals of the block.

Parameterization — Block parameterization
`Specify from a datasheet` (default) | `Specify using equation parameters directly` | `Lookup table (2-D, temperature independent)` | `Lookup table (3-D, temperature dependent)`

Select one of the following methods for block parameterization:

Specify from a datasheet — Provide the drain-source on resistance and the corresponding drain current and gate-source voltage. The block calculates the transistor gain for the Shichman and Hodges equations from this information.
Specify using equation parameters directly — Provide the transistor gain.
Lookup table (2-D, temperature independent) — Use 2-D table lookup for drain-source current as a function of gate-source voltage and drain-source voltage.
Lookup table (3-D, temperature dependent) — Use 3-D table lookup for drain-source current as a function of gate-source voltage, drain-source voltage, and temperature.

Number of terminals to Four.
Modeling option to Threshold-based or Threshold-based with thermal.

Bulk ohmic resistance — Transistor bulk resistance
`2e-3` `Ohm` (default) | nonnegative scalar

Transistor body resistance, that is, the series resistance associated with the bulk contact.

Dependencies

To enable this parameter, set:

Number of terminals to Four.
Modeling option to Surface-potential-based or Surface-potential-based with thermal.

To enable this parameter, set:

Number of terminals to Four.
Modeling option to Threshold-based or Threshold-based with thermal.

Number of terminals to Four.
Modeling option to Threshold-based or Threshold-based with thermal.

Capacitance

To enable this setting, set Modeling option to Threshold-based or Threshold-based with thermal.

Parameterization — Capacitance parameterization
`Specify fixed input, reverse transfer, and output capacitance` (default) | `Specify fixed gate-source, gate-drain, and drain-source capacitance` | `Specify tabulated input, reverse transfer, and output capacitance` | `Specify tabulated gate-source, gate-drain, and drain-source capacitance`

Select one of the following methods for capacitance parameterization:

Specify fixed input, reverse transfer, and output capacitance — Provide fixed parameter values from datasheet and let the block convert the input, output, and reverse transfer capacitance values to capacitance values, as described in Charge Model for Threshold-Based Modeling Option.
Specify fixed gate-source, gate-drain, and drain-source capacitance — Provide fixed values for capacitance parameters directly.
Specify tabulated input, reverse transfer, and output capacitance — Provide tabulated capacitance and drain-source voltage values based on datasheet plots. The block converts the input, output, and reverse transfer capacitance values to capacitance values, as described in Charge Model for Threshold-Based Modeling Option.
Specify tabulated gate-source, gate-drain, and drain-source capacitance — Provide tabulated values for capacitances and drain-source voltage.

Corresponding gate-source voltages, Vgs — Corresponding gate-source voltages
`0` `V` (default)

Gate-source voltages corresponding to the tabulated capacitance values.

The two fixed capacitance options let you model gate capacitance as a fixed gate-source capacitance C_GS and either a fixed or a nonlinear gate-drain capacitance C_GD. Select whether the gate-drain capacitance is fixed or nonlinear:

Gate-drain capacitance is constant — The capacitance value is constant and defined according to the selected parameterization option, either directly or derived from a datasheet.
Gate-drain charge function is nonlinear — The gate-drain charge relationship is defined according to the piecewise-nonlinear function described in Charge Model for Threshold-Based Modeling Option. Two additional parameters appear to let you define the gate-drain charge function.

Dependencies

To enable this parameter, in the Main setting, set Number of terminals to Four.

To enable the Separate gate-bulk and gate-source capacitance option, in the Capacitance setting, set Parameterization to Specify fixed gate-source, gate-drain, and drain-source capacitance or Specify tabulated gate-source, gate-drain, and drain-source capacitance

Channel Capacitances

To enable this setting, set Modeling option to Surface-potential-based or Surface-potential-based with thermal.

Oxide capacitance — Oxide capacitance
`1500` `pF` (default)

The parallel plate gate-channel capacitance.

Gate-source overlap capacitance — Gate-source overlap capacitance
`100` `pF` (default)

The fixed, linear capacitance associated with the overlap of the gate electrode with the source well.

Gate-drain overlap capacitance — Gate-drain overlap capacitance
`14` `pF` (default)

The fixed, linear capacitance associated with the overlap of the gate electrode with the drain well.

Body Diode

Transit time, TT — Transit time
`50e-9` `s` (default)

The time designated by the τ symbol in the body-diode equations.

Diode forward currents, If — Diode forward currents temperature independent
`[.1, .2, .5, 1, 2, 4, 7, 10]` `A` (default)

Tabulated values of the forward currents.

Dependencies

To enable this parameter, in the Body diode setting, set Model body diode to Tabulated I-V curve and Table type to Table in Vf(If) form or Table in Vf(Tj,If) form.

Diode forward currents, If(Vf) — Diode forward currents tabulated with forward voltages
`[.07, .12, .19, 1.75, 4.24, 7.32, 11.2]` `A` (default)

Tabulated values of the forward current, as a function of the forward voltages.

Dependencies

To enable this parameter,

In the Main setting, set Parameterization to Specify from a datasheet, Specify from equation parameters directly, or Lookup table (2-D, temperature independent).
In the Body diode setting, set:
- Model body diode to Tabulated I-V curve.
  Table type to Table in If(Vf) form.

In the Main setting, set Parameterization to Lookup table (3-D, temperature dependent).
In the Body diode setting, set:
- Model body diode to Tabulated I-V curve.
  Table type to Table in If(Tj,Vf) form.

Diode forward voltages, If(Tj,Vf) — Diode forward voltages temperature dependent
`[.9, 1.15, 1.25, 1.5, 1.75, 2.17, 2.6, 2.85; .58, .68, .75, 1.1, 1.38, 1.77, 2.27, 2.7]` `V` (default)

Tabulated values of the forward voltage, as a function of the forward currents and junction temperatures.

Dependencies

To enable this parameter,

In the Main setting, set Parameterization to Lookup table (3-D, temperature dependent).
In the Body diode setting, set:
- Model body diode to Tabulated I-V curve.
  Table type to Table in Vf(Tj,If) form.

Diode off conductance — Conductance of diode when reverse biased
`1e-12` `1/Ohm` (default) | positive scalar

Since R2024a

Conductance of the diode when it is reverse biased.

Dependencies

To enable this parameter, set Model body diode to Tabulated I-V curve.

Temperature Dependence (Threshold-Based Modeling Option)

This configuration of the Temperature Dependence setting corresponds to the threshold-based block modeling option, which is the default. If you are using the surface-potential-based modeling option of the block, see Temperature Dependence (Surface-Potential-Based Modeling Option)

Parameterization — Temperature dependance parameterization
`None — Simulate at parameter measurement temperature` (default) | `Model temperature dependence`

Select one of the following methods for temperature dependence parameterization:

None — Simulate at parameter measurement temperature — Temperature dependence is not modeled. This is the default method.
Model temperature dependence — Model temperature-dependent effects. Provide a value for simulation temperature, T_s, a value for BEX, and a value for the measurement temperature T_m1 (using the Measurement temperature parameter on the Main setting). You also have to provide a value for α using one of two methods, depending on the value of the Parameterization parameter on the Main setting. If you parameterize the block from a datasheet, you have to provide R_DS(on) at a second measurement temperature, and the block will calculate α based on that. If you parameterize by specifying equation parameters, you have to provide the value for α directly.

None — Simulate at parameter measurement temperature — Temperature dependence is not modeled.
Model temperature dependence — Model temperature-dependent effects. Provide a value for the device simulation temperature, T_s, and the temperature-scaling coefficients for other block parameters.

Gain temperature exponent — Gain temperature exponent
`1.3` (default)

The MOSFET gain, β, is assumed to scale exponentially with temperature, β = β _m1(T_m1/T_s)^η_β. β_m1 is the value of the Gain parameter from the Main setting and η_β is the Gain temperature exponent.

Flatband voltage temperature coefficient — Flatband voltage temperature coefficient
`5e-4` `V/K` (default)

The flatband voltage, V_FB, is assumed to scale linearly with temperature, V_FB = V_FBm1 + (T_s – T_m1)S_{T,V_FB}. V_FBm1 is the value of the Flatband voltage parameter from the Main setting and S_{T,V_FB} is the Flatband voltage temperature coefficient.

Surface potential at strong inversion temperature coefficient — Surface potential at strong inversion temperature coefficient
`-8.5e-4` `V/K` (default)

The surface potential at strong inversion, 2ϕ_B, is assumed to scale linearly with temperature, 2ϕ_B = 2ϕ_Bm1 + (T_s – T_m1)S_{T,ϕ_B}. 2ϕ_Bm1 is the value of the Surface potential at strong inversion parameter from the Main setting and S_{T,ϕ_B} is the Surface potential at strong inversion temperature coefficient.

Velocity saturation temperature exponent — Velocity saturation temperature exponent
`1.04` (default)

The velocity saturation, θ_sat, is assumed to scale exponentially with temperature, θ_sat = θ_sat,m1 (T_m1/T_s)^η_θ. θ_sat,m1 is the value of the Velocity saturation factor parameter from the Main setting and η_θ is the Velocity saturation temperature exponent.

Surface roughness scattering temperature exponent — Surface roughness scattering temperature exponent
`0.65` (default)

This parameter leads to a temperature-dependent reduction in the MOSFET transconductance at high gate voltage. The surface roughness scattering, θ_sr, is assumed to scale exponentially with temperature, θ_sr = θ_sr,m1 (T_m1/T_s)^η_sr. θ_sr,m1 is the value of the Surface roughness scattering factor parameter from the Main setting and η_sr is the Surface roughness scattering temperature exponent.

Resistance temperature exponent — Resistance temperature exponent
`0.95` (default)

The series resistances are assumed to correspond to semiconductor resistances. Therefore, they decrease exponentially with increasing temperature. R_i = R_i,m1 (T_m1/T_s)^η_R, where i is S, D, or G, for the source, drain, or gate series resistance, respectively. R_i,m1 is the value of the corresponding series resistance parameter from the Ohmic Resistance setting and η_R is the Resistance temperature exponent.

Body diode reverse saturation current temperature exponent — Body diode reverse saturation current temperature exponent
`3` (default)

$I_{s} = I_{s, m 1} {(\frac{T_{s}}{T_{m 1}})}^{η_{I s}} \cdot \exp (\frac{E_{G}}{k_{B}} \cdot (\frac{1}{T_{m 1}} - \frac{1}{T_{s}})) .$

I_s,m1 is the value of the Reverse saturation current parameter from the Body Diode setting, k_B is Boltzmann’s constant (8.617x10^-5eV/K), and η_Is is the Body diode reverse saturation current temperature exponent. The default value is 3, because N_C for silicon is roughly proportional to T^3/2. You can remedy the effect of neglecting the temperature-dependence of the bandgap by a pragmatic choice of η_Is.

Device simulation temperature — Device simulation temperature
`25` `°C` (default)

Temperature T_s at which the device is simulate.

Faults

The fault interface includes the Fault Inspector window and the Faults section of the Blocks tab for blocks that support faults. You define what triggers the fault and how the fault behaves when that trigger occurs. When you create and edit the fault, you parameterize the fault behavior.

To add a fault, click the Add fault hyperlink.

After you create the fault, you can change the properties in the Fault Inspector window. When you open a block that has a fault, the Open Fault Inspector hyperlink appears instead of the Add fault hyperlink. For an example that shows how to include faults, see Analyze a DC Armature Winding Fault.

To enable this parameter:

In the Fault Inspector window, set Trigger Type to Behavioral.
In the Main setting, set Number of terminals to Four.

Set Model body diode to either Exponential or Tabulated I-V curve.
In the Fault Inspector window, set Trigger Type to Behavioral.