反復学習制御

反復学習制御 (ILC) とは、同じ初期操作条件から開始される反復処理を実行するシステムのパフォーマンスを改善する場合に役立つ制御手法です。この手法では、前回のバッチ実行の頻繁な測定値を誤差軌跡の形式で使用して、後続のバッチ実行の制御信号を更新します。ILC の用途には、製造、ロボティクス、および化学処理の業種で実際に稼働している多数の産業用システムが含まれます。これらの業種では、組み立てラインでの大量生産に反復を伴います。このため、反復タスクまたは反復的な外乱があり、前回の反復からの知識を使用して次回の反復を改善する場合に ILC を使用します。

一般的な ILC の更新則は次の形式を取ります ([1] および [2]):

$u_{k+1}(t)=Q(q)[u_k(t)+L(q)e_k(t+1)].$

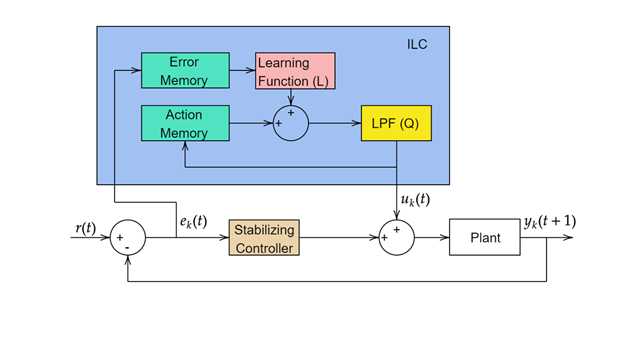
ここで、Q は制御チャタリングを除去するローパス フィルター、L は学習関数です。k は k 回目の反復を表します。学習関数を設計する複数の方法があります。

ILC を Simulink^® で実装するには、Iterative Learning Control ブロックを使用します。このブロックを使用して、モデルに依存しない ILC、またはモデルベースの ILC を実装できます。

モデルに依存しない ILC

モデルに依存しない ILC にはシステム ダイナミクスに関する事前情報が不要で、比例-微分 (PD) の誤差フィードバックを使用して制御履歴を更新します。この方法は、SISO システムのみに適用できます。

モデルに依存しない ILC の更新則は次のとおりです。

$$u_{k+1}(t)=Q(q)\left(u_k(t)+{\gamma }_p{e}_k(t+1)+{\gamma }_d(e_k(t+1)-e_k(t))\right).$$

ここで、γ_p と γ_d はそれぞれ、比例ゲインと微分ゲインです。ゲインの選択により、P タイプ、D タイプ、または PD タイプの ILC を実装できます。ゲイン γ_p および γ_d は、ILC が反復間でどの程度よく学習するかを決定します。ILC のゲインが大きすぎる場合、閉ループ システムが不安定になることがあります (ロバスト性)。ILC のゲインが小さすぎる場合、収束が遅くなることがあります (パフォーマンス)。ILC のゲインを適切に調整することにより、追跡誤差のノミナル値を漸近的にゼロに収束させることができます。

モデルベースの ILC

この方法はより一般的な ILC の形式であり、次の形式を取る SISO および MIMO の LTI 状態空間システムに適用できます。

$$\begin{array}{l}\begin{array}{cc}{x}_k(t+1)=A{x}_k(t)+B{u}_k(t),& x(0)=x_0,\end{array}\\ y_k(t)=C{x}_k(t).\end{array}$$

この方法では、プラント入出力行列 G に基づいて、学習関数 L を設計します。プラント ダイナミクスから、入力と出力の関係 Y_k = GU_k + d を定義できます。ここで、以下となります。

$$\begin{array}{l}\begin{array}{cc}{Y}_k=\left[\begin{array}{c}y(t+1)\\ y(t+2)\\ ⋮\\ y(t+N)\end{array}\right],& U_k=\left[\begin{array}{c}u(t)\\ u(t+2)\\ ⋮\\ u(t+N-1)\end{array}\right]\end{array}\\ G=\left[\begin{array}{cccc}CB& 0& \cdots & 0\\ CAB& CB& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮\\ C{A}^{N-1}B& C{A}^{N-2}B& \cdots & CB\end{array}\right],\\ d=\left[\begin{array}{cccc}CA{x}_0& C{A}^2{x}_0& \cdots & C{A}^N{x}_0\end{array}\right].\end{array}$$

さらに、誤差ダイナミクスを次のように記述できます。

$$e_{k+1}=(I-GL)e_k.$$

Iterative Learning Control ブロックでは、勾配ベースと逆モデル ベースの 2 種類のモデルベース ILC が用意されています。

勾配ベースの ILC 則

勾配ベースの ILC では、学習関数 L = γG^T で入出力行列の転置を使用します。したがって、ILC 制御則は次になります。

$u_{k+1}(t)=Q(q)[u_k(t)+\gamma G^T{e}_k(t+1)]$

誤差ダイナミクスは次になります。

$$e_{k+1}=(I-\gamma G{G}^T)e_k$$

ここで、γ は ILC ゲインです。誤差の収束は、ゲインの選択によって決まります。この方法では、|1 – γGG^T| < 1 により確実に誤差が収束します。このため、最も速く収束させるために γ = 1/|G²| を指定できます。

逆モデル ベースの ILC 則

逆モデル ベースの ILC では、学習関数 L = γG^-1 で入出力行列の逆行列を使用します。したがって、ILC 制御則は次になります。

$u_{k+1}(t)=Q(q)[u_k(t)+\gamma G^{-1}{e}_k(t+1)].$

行列 G が正方でない場合、ブロックでは代わりに疑似逆行列が使用されます。

誤差ダイナミクスは次になります。

$$e_{k+1}=(I-\gamma G{G}^{-1})e_k$$

この方法では、|1 – γ| < 1 により確実に誤差が収束します。このため、収束させるには 2 未満の正のスカラーを指定します。

参照

[1] Bristow, Douglas A., Marina Tharayil, and Andrew G. Alleyne. “A Survey of Iterative Learning Control.” IEEE Control Systems 26, no. 3 (June 2006): 96–114. https://doi.org/10.1109/MCS.2006.1636313.

[2] Gunnarsson, Svante, and Mikael Norrlöf. A Short Introduction to Iterative Learning Control. Linköping University Electronic Press, 1997.

[3] Hätönen, J., T.J. Harte, D.H. Owens, J. Ratcliffe, P. Lewin, and E. Rogers. “Discrete-Time Arimoto ILC-Algorithm Revisited.” IFAC Proceedings Volumes 37, no. 12 (August 2004): 541–46.

[4] Lee, Jay H., Kwang S. Lee, and Won C. Kim. “Model-Based Iterative Learning Control with a Quadratic Criterion for Time-Varying Linear Systems.” Automatica 36, no. 5 (May 1, 2000): 641–57.

[5] Harte, T. J., J. Hätönen, and D. H. Owens *. “Discrete-Time Inverse Model-Based Iterative Learning Control: Stability, Monotonicity and Robustness.” International Journal of Control 78, no. 8 (May 20, 2005): 577–86.

[6] Zhang, Yueqing, Bing Chu, and Zhan Shu. “A Preliminary Study on the Relationship Between Iterative Learning Control and Reinforcement Learning⁎.” IFAC-PapersOnLine, 13th IFAC Workshop on Adaptive and Learning Control Systems ALCOS 2019, 52, no. 29 (January 1, 2019): 314–19. https://doi.org/10.1016/j.ifacol.2019.12.669.

参考

Iterative Learning Control

トピック

• Iterative Learning Control of a Single-Input Single-Output System
• Model Based Iterative Learning Control of Multi-Input Multi-Output System