アクティブな外乱の抑制の制御

アクティブな外乱の抑制の制御 (ADRC) は、ダイナミクスおよび内部と外部の外乱が不明なプラント用のコントローラーを設計するのに役立つ、モデルに依存しない制御手法です。このアルゴリズムでは、オーバーシュートのないロバストな外乱の抑制を提供するコントローラーを設計するためにプラントダイナミクスの近似のみが必要です。

Active Disturbance Rejection Control ブロックを使用して ADRC を実装できます。このブロックは、不明なダイナミクスと外乱をプラントの拡張状態としてモデル化するとともに、既知のシステムダイナミクスの 1 次または 2 次のモデル近似を使用します。通常、動作範囲内のプラントの開ループステップ応答からこの次数を決定します。

1 次近似 — $\dot{y} (t) = b_{0} u (t) + f (t)$
2 次近似 — $\ddot{y} (t) = b_{0} u (t) + f (t)$

ここで

y(t) はプラント出力です。
u(t) は入力信号です。
b₀ は臨界ゲインです。これは、入力 u(t) に対するプラント応答を記述する推定ゲインです。
f(t) は外乱の合計です。これには、不明なダイナミクスおよびその他の外乱が含まれます。

ブロックは拡張状態オブザーバー (ESO) を使用して f(t) を推定し、モデル近似の既知の部分に対する推定された外乱の影響を低減することで、外乱の抑制制御を実装します。

離散時間および連続時間の両方のコントローラーを実装できます。プラントモデルの時間領域に合わせて、コントローラーの時間領域およびサンプル時間を設定します。

コントローラーの構造

1 次近似

1 次のプラントモデル近似 $\dot{y} (t) = b_{0} u (t) + f (t)$ では、プラント出力状態は x₁ = y(t) で、拡張状態は x₂ = f(t) です。

状態空間モデルは以下のとおりです。

$\begin{array}{l} \dot{x} = A x + B u + (\begin{matrix} 0 \\ \dot{f} (t) \end{matrix}) \\ y = C x, \end{array}$

ここで

$A = (\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}), B = (\begin{matrix} b_{0} \\ 0 \end{matrix}), C = (\begin{matrix} 1 & 0 \end{matrix}) .$

この観測可能なシステムでは、ブロックはルーエンバーガーオブサーバーを使用して、プラントの状態および外乱の合計の推定を提供します。推定状態の使用

$\begin{array}{l} z_{1} = \hat{y} (t) \\ z_{2} = \hat{f} (t), \end{array}$

コントローラーは、制御入力 u(t) を次のように計算します。

$u (t) = \frac{u_{0} (t) - z_{2}}{b_{0}},$

ここで

$u_{0} (t) = K_{P} (r (t) - z_{1}) .$

これは推定ベースの状態フィードバックコントローラーであり、推定値と実際の値が等しい場合、システムは 1 次閉ループ動作になります。この閉ループシステムでは、極 s = –K_P となります。

このコントローラーは、以下の制御構造として表されます。

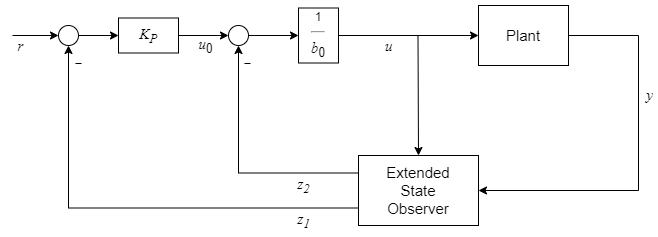
Control loop structure for active disturbance rejection control for first-order model approximation.

コントローラーの調整を簡素化するために、ブロックではコントローラーの極を (s + ω_c) に設定し、オブザーバーの極を (s + ω_o)² に設定します。ここで、ω_c および ω_o はそれぞれ、コントローラーとオブザーバーの帯域幅です。

2 次近似

2 次のプラントモデル近似 $\ddot{y} (t) = b_{0} u (t) + f (t)$ では、プラント出力状態は x₁ = y(t) および x₂ = $\dot{y} (t)$ で、拡張状態は x₃ = f(t) です。

状態空間モデルは以下のとおりです。

$\begin{array}{l} \dot{x} = A x + B u + (\begin{matrix} 0 \\ 0 \\ \dot{f} (t) \end{matrix}) \\ y = C x, \end{array}$

ここで

$A = (\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{matrix}), B = (\begin{matrix} 0 \\ b_{0} \\ 0 \end{matrix}), C = (\begin{matrix} 1 & 0 & 0 \end{matrix}) .$

$\begin{array}{l} z_{1} = \hat{y} (t) \\ z_{2} = \hat{\dot{y}} (t) \\ z_{3} = \hat{f} (t), \end{array}$

コントローラーは、制御入力 u(t) を次のように計算します。

$u (t) = \frac{u_{0} (t) - z_{3}}{b_{0}},$

ここで

$u_{0} (t) = K_{P} (r (t) - z_{1}) - K_{D} z_{2} .$

これは推定ベースの状態フィードバックコントローラーであり、推定値と実際の値が等しい場合、システムは 2 次閉ループ動作になります。

このコントローラーは、以下の制御構造として表されます。

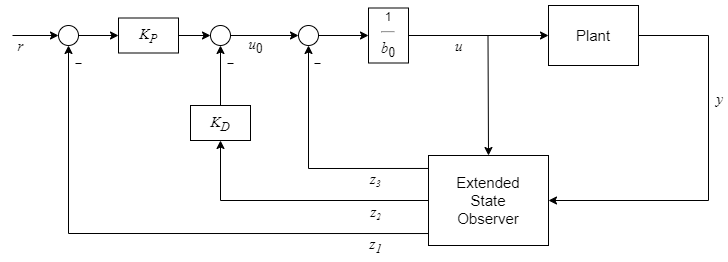
Control loop structure for active disturbance rejection control for second-order model approximation.

コントローラーの調整を簡素化するために、ブロックではコントローラーの極を (s + ω_c)² に設定し、オブザーバーの極を (s + ω_o)³ に設定します。ここで、ω_c および ω_o はそれぞれ、コントローラーとオブザーバーの帯域幅です。

コントローラーのパラメーターの指定

プラントの ADRC を実装するには、プラント近似の臨界ゲイン値 b₀ の妥当な推定を提供することが重要です。そうするための 1 つの手法は以下のとおりです。

振幅 u_OL のステップ信号を使用して、動作範囲において開ループでプラントをシミュレートします。
短期間のプラント出力の変化を記録します。
- 1 次 ADRC では、応答近似 y = at を使用し、以下のように a を求めます。
  $a = \frac{y (e n d) - y (0)}{t (e n d) - t (0)}$
  例については、Design Active Disturbance Rejection Control for Water-Tank Systemを参照してください。
- 2 次 ADRC では、応答近似 y = ½at² を使用し、以下のように a を求めます。
  $a = \frac{2 (y (e n d) - y (0))}{{(t (e n d) - t (0))}^{2}}$
  例については、Design Active Disturbance Rejection Control for Boost Converterを参照してください。
次に、b₀ を a およびステップ振幅 u_OL から求めることができます。
$b_{0} = \frac{a}{u_{O L}}$
[臨界ゲイン] パラメーターを使用して、ブロックパラメーターでこの値を設定します。

次に、コントローラーの応答を調整するために、ω_c および ω_o の値を、それぞれ [コントローラー帯域幅] および [オブザーバー帯域幅] を使用して指定します。これらの値は、コントローラーのパフォーマンス要件によって異なります。一般的に、高速な応答ほど、必要なコントローラーの帯域幅が大きくなります。また、オブザーバーはコントローラーよりも迅速に収束する必要があります。したがって、オブザーバーの帯域幅はコントローラーの帯域幅の 5 ～ 10 倍に設定します。

さらに、ブロックでは状態の初期状態の指定、コントローラーの出力の制限、および推定状態値の出力を行うことができます。

参照

[1] Han, Jingqing. “From PID to Active Disturbance Rejection Control.” IEEE Transactions on Industrial Electronics 56, no. 3 (March 2009): 900–906. https://doi.org/10.1109/TIE.2008.2011621.

[2] Herbst, Gernot. “A Simulative Study on Active Disturbance Rejection Control (ADRC) as a Control Tool for Practitioners.” Electronics 2, no. 3 (August 15, 2013): 246–79. https://doi.org/10.3390/electronics2030246.

[3] Zhiqiang Gao. “Scaling and Bandwidth-Parameterization Based Controller Tuning.” In Proceedings of the 2003 American Control Conference, 2003, 6:4989–96. Denver, CO, USA: IEEE, 2003. https://doi.org/10.1109/ACC.2003.1242516.

参考

Active Disturbance Rejection Control