HL-20 機体の平衡化と線形化

この例では次を使用します。

これは、HL-20 機体用の飛行制御システムの設計と調整に関する 5 部構成の例のシリーズのパート 1 です。このパートでは、機体の平衡化と線形化について説明します。

HL-20 モデル

HL-20 モデルは、NASA HL-20 Lifting Body Airframe (Aerospace Blockset)で説明されているモデルを応用したものです。これは飛行の最終降下と着陸のフェーズにおける機体の 6-DOF モデルです。このフェーズでは推力を使用せず、機体は滑走路に向けて滑空しています。

open_system('csthl20_trim')

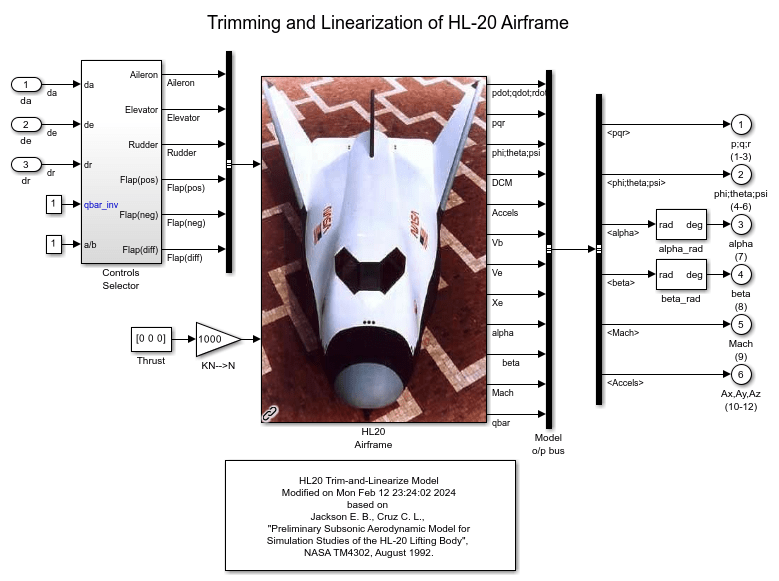
このバージョンのモデルには、運動方程式 (EOM)、空力テーブルを用いた力とモーメントの計算、環境モデル、および補助翼、昇降舵、方向舵の要求を 6 つのコントロールサーフェスの偏向角にマッピングする "Controls Selector" ブロックが含まれています。

バッチ平衡化

平衡化では、機体の力とモーメントがゼロになる補助翼、昇降舵および方向舵の偏向角が計算されます。これは、機体の速度 ub、vb、wb および角速度 p、q、r を定常状態に保つことと等価です。降下中は推力が使用されないため、自由度 1 が失われ、平衡化条件を緩和して ub を変化させなければなりません。偏向角 da、de、dr の平衡値は、風に対する機体の方向により異なります。この方向は迎角 (AoA) alpha と横滑り角 (AoS) beta によって特徴付けられます。

関数 operspec と関数 findop を使用して、機体の操作範囲をカバーする (alpha,beta) 値のグリッド上で平衡偏向角を効率的に計算することができます。ここでは -10 ～ 25 度の 8 つの alpha 値と、-10 ～ +10 度の 5 つの beta 値に対してモデルを平衡化します。ノミナルの高度と速度はそれぞれ 10,000 フィートとマッハ 0.6 に設定します。

d2r = pi/180;            % degrees to radians
m2ft = 3.28084;          % meter to feet
Altitude = 10000/m2ft;   % Nominal altitude
Mach = 0.6;              % Nominal Mach
alpha_vec = -10:5:25;	 % Alpha Range
beta_vec = -10:5:10;     % Beta Range
[alpha,beta] = ndgrid(alpha_vec,beta_vec);   % (Alpha,Beta) grid

操作点仕様の配列を作成するには operspec を使用します。

opspec = operspec('csthl20_trim',size(alpha));

opspec(1)

ans = 


 Operating point specification for the Model csthl20_trim.
 (Time-Varying Components Evaluated at time t=0)

States: 
----------
     x         Known    SteadyState     Min         Max        dxMin       dxMax   
___________ ___________ ___________ ___________ ___________ ___________ ___________
                                                                                   
(1.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/Calculate DCM & Euler Angles/phi theta psi
     0         false       true        -Inf         Inf        -Inf         Inf    
 -0.19945      false       true        -Inf         Inf        -Inf         Inf    
     0         false       true        -Inf         Inf        -Inf         Inf    
(2.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/p,q,r 
     0         false       true        -Inf         Inf        -Inf         Inf    
     0         false       true        -Inf         Inf        -Inf         Inf    
     0         false       true        -Inf         Inf        -Inf         Inf    
(3.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/ub,vb,wb
  202.67       false       true        -Inf         Inf        -Inf         Inf    
     0         false       true        -Inf         Inf        -Inf         Inf    
  23.257       false       true        -Inf         Inf        -Inf         Inf    
(4.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/xe,ye,ze
-12071.9115    false       true        -Inf         Inf        -Inf         Inf    
     0         false       true        -Inf         Inf        -Inf         Inf    
-3047.9999     false       true        -Inf         Inf        -Inf         Inf    

Inputs: 
----------
  u   Known  Min   Max 
_____ _____ _____ _____
                       
(1.) csthl20_trim/da
  0   false -Inf   Inf 
(2.) csthl20_trim/de
  0   false -Inf   Inf 
(3.) csthl20_trim/dr
  0   false -Inf   Inf 

Outputs: 
----------
  y   Known  Min   Max 
_____ _____ _____ _____
                       
(1.) csthl20_trim/p;q;r (1-3)
  0   false -Inf   Inf 
  0   false -Inf   Inf 
  0   false -Inf   Inf 
(2.) csthl20_trim/phi;theta;psi (4-6)
  0   false -Inf   Inf 
  0   false -Inf   Inf 
  0   false -Inf   Inf 
(3.) csthl20_trim/alpha (7)
  0   false -Inf   Inf 
(4.) csthl20_trim/beta (8)
  0   false -Inf   Inf 
(5.) csthl20_trim/Mach (9)
  0   false -Inf   Inf 
(6.) csthl20_trim/Ax,Ay,Az (10-12)
  0   false -Inf   Inf 
  0   false -Inf   Inf 
  0   false -Inf   Inf

機体の各方向について平衡条件を指定します。このためには、次を行います。

出力 alpha および beta をそれぞれの目的値に固定して、方向を指定します。
マッハ出力を 0.6 に固定して、機体速度を指定します。
角速度 p、q、r を定常としてマークします。
速度 vb および wb を定常としてマークします。

for ct=1:40
   % Specify alpha angle
   opspec(ct).Outputs(3).y = alpha(ct);
   opspec(ct).Outputs(3).Known = true;
   % Specify beta angle
   opspec(ct).Outputs(4).y = beta(ct);
   opspec(ct).Outputs(4).Known = true;
   % Specify Mach speed
   opspec(ct).Outputs(5).y = Mach;
   opspec(ct).Outputs(5).Known = true;
   % Mark p,q,r as steady
   opspec(ct).States(2).SteadyState = true(3,1);
   % Mark vb,wb as steady
   opspec(ct).States(3).SteadyState = [false;true;true];
   % (phi,theta,psi) and (Xe,Ye,Ze) are not steady
   opspec(ct).States(1).SteadyState = false(3,1);
   opspec(ct).States(4).SteadyState = false(3,1);
end

平衡化の条件を完全に特徴付けるために次も行います。

p=0 を設定して、ローリングを回避します。
ロール角、ピッチ角、ヨー角 (phi,theta,psi) を (0,alpha,beta) に設定して、風座標系と地球座標系を揃えます。
機体の位置 (Xe,Ye,Ze) を (0,0,-Altitude) に指定します。

for ct=1:40
   % Set (phi,theta,psi) to (0,alpha,beta)
   opspec(ct).States(1).x = [0 ; alpha(ct)*d2r ; beta(ct)*d2r];
   opspec(ct).States(1).Known = true(3,1);
   % Set p=0 (no rolling)
   opspec(ct).States(2).x(1) = 0;
   opspec(ct).States(2).Known(1) = true;
   % Set (Xe,Ye,Ze) to (0,0,-Altitude)
   opspec(ct).States(4).x = [0 ; 0 ; -Altitude];
   opspec(ct).States(4).Known = true(3,1);
end

次に findop を使用して、(alpha,beta) の 40 個の組み合わせすべての平衡化条件を一度に計算します。このバッチモードによる方法ではモデルが 1 回コンパイルされます。FINDOP は最適化を使って各平衡を特徴付ける非線形方程式を解きます。ここではこのタスクに "SQP" アルゴリズムを使用します。

% Set options for FINDOP solver
TrimOptions = findopOptions;
TrimOptions.OptimizationOptions.Algorithm = 'sqp';
TrimOptions.DisplayReport = 'off';

% Trim model
[ops,rps] = findop('csthl20_trim',opspec,TrimOptions);

これにより 8 行 5 列の配列 OPS (操作条件) および RPS (最適化レポート) が返されます。RPS を使用して、各平衡化条件が正しく計算されたことを確認できます。以下は最初の (alpha,beta) ペアの結果を示しています。

[alpha(1) beta(1)]

ans =

   -10   -10

ops(1)

ans = 


 Operating point for the Model csthl20_trim.
 (Time-Varying Components Evaluated at time t=0)

States: 
----------
    x     
__________
          
(1.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/Calculate DCM & Euler Angles/phi theta psi
    0     
 -0.17453 
 -0.17453 
(2.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/p,q,r 
    0     
 -0.15825 
 0.008004 
(3.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/ub,vb,wb
 191.0911 
 -34.2143 
 -33.6945 
(4.) csthl20_trim/HL20 Airframe/6DOF (Euler Angles)/xe,ye,ze
    0     
    0     
-3047.9999

Inputs: 
----------
   u    
________
        
(1.) csthl20_trim/da
-23.9841
(2.) csthl20_trim/de
-6.4896 
(3.) csthl20_trim/dr
 4.0858

rps(1).TerminationString

ans =

    'Operating point specifications were successfully met.'

バッチ線形化

通常、飛行制御システムのゲインは alpha と beta の関数としてスケジュールされます。詳細については、パート 2 (HL-20 の自動操縦における角速度の制御) を参照してください。これらのゲインを調整するには、40 の平衡化条件における HL-20 機体の線形化モデルが必要です。linearize を使用して、平衡化の操作条件 ops からこれらのモデルを計算します。

% Linearize airframe dynamics at each trim condition
G = linearize('csthl20_trim','csthl20_trim/HL20 Airframe',ops);

size(G)

8x5 array of state-space models.
Each model has 34 outputs, 9 inputs, and 12 states.

"Controls Selector" ブロックの線形バージョンは、昇降舵の偏向の量に依存し、qbar_inv=1 (ノミナル動的圧力 Mach=0.6) について計算する必要があります。便宜上、このブロックも 40 の平衡化条件で線形化します。

CS = linearize('csthl20_trim','csthl20_trim/Controls Selector',ops);

% Zero out a/b and qbar_inv channels
CS = [CS(:,1:3) zeros(6,2)];

線形モデルの簡略化

線形化された機体モデルには、次のように 12 の状態があります。

xG = G.StateName

xG =

  12x1 cell array

    {'phi theta psi(1)'}
    {'phi theta psi(2)'}
    {'phi theta psi(3)'}
    {'p,q,r (1)'       }
    {'p,q,r (2)'       }
    {'p,q,r (3)'       }
    {'ub,vb,wb(1)'     }
    {'ub,vb,wb(2)'     }
    {'ub,vb,wb(3)'     }
    {'xe,ye,ze(1)'     }
    {'xe,ye,ze(2)'     }
    {'xe,ye,ze(3)'     }

これにはロール/ピッチ/ヨー自動操縦の制御下にない状態や、この自動操縦の設計にほとんど寄与しない状態も含まれています。制御目的の場合、最も重要な状態は、ロール角 phi、機体の速度 ub、vb、wb、および角速度 p、q、r です。したがって、modred を使用して、これらの状態のみを保持する 7 次モデルを取得します。

G7 = G;
xKeep = {...
   'phi theta psi(1)'
   'ub,vb,wb(1)'
   'ub,vb,wb(2)'
   'ub,vb,wb(3)'
   'p,q,r(1)'
   'p,q,r(2)'
   'p,q,r(3)'};
[~,xElim] = setdiff(xG,xKeep);
for ct=1:40
   G7(:,:,ct) = modred(G(:,:,ct),xElim,'truncate');
end

これらの線形化モデルが得られたら、飛行制御システムゲインの調整とスケジューリングのタスクに進むことができます。この例のパート 2 については、HL-20 の自動操縦における角速度の制御を参照してください。

HL-20 機体の平衡化と線形化

HL-20 モデル

バッチ平衡化

バッチ線形化

線形モデルの簡略化

関連するトピック