1 つの油圧シリンダーのシミュレーション

モデルを開く

この例では、Simulink® を使用して油圧シリンダーをモデル化する方法を示します。これらのコンセプトは、油圧動作をモデル化する必要のあるさまざまな用途に適用可能です。

モデルの解析と物理現象

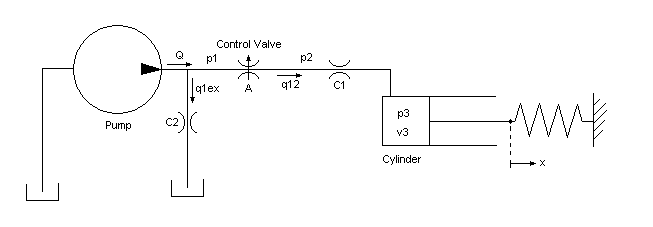
次の概略図は油圧シリンダーのモデルを示したものです。このモデルでは、ポンプ流量 Q が供給圧 p1 に向けられ、ここから層流 q1ex が漏れて排出されます。ピストン/シリンダー アセンブリの制御バルブは、可変面積の開口部を通過する乱流としてモデル化されます。その流量 q12 によって中間圧力 p2 に達しますが、圧力はその後、アクチュエータ シリンダーにつながるラインで降下します。シリンダー圧力 p3 により、ピストンはバネ荷重に逆らって動き、位置が x になります。

ポンプ出力で、流れは漏れと制御バルブへの流れに分かれます。モデルでは、方程式セット 1 の方程式を使用して、漏れ q1ex を層流としてシミュレートしています。

方程式セット 1

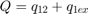
$$Q=q_{12}+q_{1ex}$$

$$q_{1ex}=C_2 \cdot p_1 $$

$$p_1=\frac{(Q-q_{12})}{C_2}$$

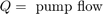
$$ Q = \mbox{ pump flow}$$

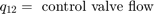
$$ q_{12} = \mbox{ control valve flow}$$

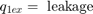
$$ q_{1ex} = \mbox{ leakage}$$

$$ C_2 = \mbox{ flow coefficient}$$

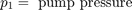
$$ p_1 = \mbox{ pump pressure}$$

制御バルブを通る乱流をシミュレートするために、モデルではオリフィスの方程式を実装しています。方程式セット 2 に示すように、符号関数と絶対値関数はどちらの方向の流れにも対応します。

方程式セット 2

$$q_{12}=C_d \cdot A \cdot sgn(p_1-p_2) \cdot \sqrt{\frac{2}{\rho}|p_1-p_2|}$$

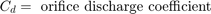
$$ C_d = \mbox{ orifice discharge coefficient} $$

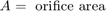
$$ A = \mbox{ orifice area} $$

$$ p_2 = \mbox{ pressure downstream of control valve} $$

$$ \rho = \mbox{ fluid density} $$

シリンダー内の流体は、流体の流れ q12 = q23 からピストン運動のコンプライアンスを引いたものによって加圧されます。モデルでは、方程式セット 3 の方程式を使用して、流体の流れと流れの圧縮率を実装しています。

方程式セット 3

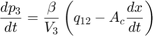
$$\frac{dp_3}{dt}=\frac{\beta}{V_3} \left(q_{12}-A_c \frac{dx}{dt}\right)$$

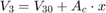
$$V_3=V_{30} + A_c \cdot x$$

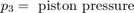
$$ p_3 = \mbox{ piston pressure} $$

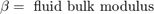
$$ \beta = \mbox{ fluid bulk modulus} $$

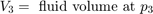
$$ V_3 = \mbox{ fluid volume at } p_3 $$

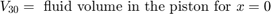
$$ V_{30}= \mbox{ fluid volume in the piston for } x = 0 $$

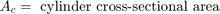
$$ A_c = \mbox{ cylinder cross-sectional area} $$

油圧力が大きいため、モデルではピストンとバネの質量は無視しています。この関係を微分し、p2 ～ p3 の圧力降下を組み込むことで、連立方程式を組み込んでいます。

方程式セット 3 では、バルブからアクチュエータへの層流をモデル化しています。方程式セット 4 では、ピストンでの力平衡が与えられています。

方程式セット 4

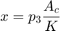
$$x=p_3\frac{A_c}{K}$$

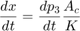
$$\frac{dx}{dt}=\frac{dp_3}{dt} \frac{A_c}{K}$$

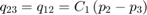
$$q_{23}=q_{12}=C_1 \left( p_2-p_3 \right)$$

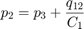
$$ p_2=p_3 + \frac{q_{12}}{C_1} $$

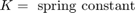
$$ K = \mbox{ spring constant} $$

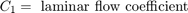
$$ C_1 = \mbox{ laminar flow coefficient} $$

シミュレーションの実行

シミュレーションを実行するには、Simulink ツールストリップで [実行] をクリックします。

このモデルは、シミュレーション中に、MATLAB ワークスペースの Simulink.SimulationOutput オブジェクト out に関連データのログを作成します。信号のログ データは sldemo_hydcyl_output という構造体の out オブジェクト内に格納されます。ログが作成された信号には青いバッジが付きます。

Pump サブシステム

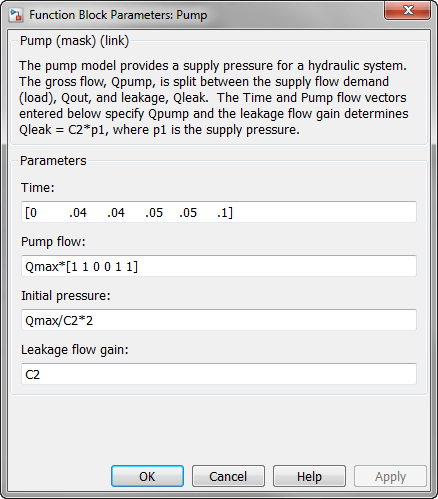
Pump サブシステムのマスク内を表示するには、Pump サブシステムを右クリックし、[マスク]、[マスク内を表示] を選択します。供給圧が、ポンプ流量と負荷 (出力) 流量の関数として計算されます。Qpump はポンプ流量データで、モデル ワークスペースに保存されています。時間点とそれに対応する流量の列ベクトルをもつ行列 [T,Q] では、流量データが指定されます。このモデルでは、圧力 p1 が方程式セット 1 に示したとおりに計算されます。Qout = q12 は制御バルブを介した p1 の 1 次関数であるため、代数ループが形成されます。初期値を p10 と推定すると、より効率的な解が得られます。

'Pump' サブシステム マスクを使用して、T、Q、p10、および C2 の各パラメーターにアクセスして変更できます。

Valve/Cylinder/Piston/Spring Assembly サブシステム

Actuator サブシステムを表示するには、マスクされた Valve/Cylinder/Piston/Spring Assembly サブシステムを右クリックし、[マスク]、[マスク内を表示] を選択します。連立微分代数方程式により、圧力 p3 でのシリンダーの加圧がモデル化されます。これは、方程式セット 3 に導関数として出てきたもので、ステート (積分器) として使用されます。ピストンの質量を無視する場合、バネの力とピストンの位置は p3 の直接の倍数であり、速度は p3 の時間微分の直接の倍数です。後者の関係により、Beta Gain ブロックの周りに代数ループが形成されます。中間圧力 p2 は、p3 と、シリンダーへとつながるバルブからの流量による圧力降下分の合計です (方程式セット 4)。また、この関係により、制御バルブと 1/C1 ゲインを通じて代数的な制約が課せられます。

制御バルブ サブシステムでは、オリフィスが計算されます (方程式セット 2)。上流圧力、下流圧力、および可変のオリフィス面積が制御バルブ サブシステムで入力として使用されます。Control Valve Flow サブシステムにより、符号付き平方根が計算されます。

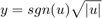
$$y=sgn(u)\sqrt{|u|}$$

サブシステムで 3 つの非線形関数が実装されていますが、そのうち 2 つは不連続です。しかし、組み合わせにより、y は u の連続関数となります。

結果

モデルのシミュレーションには、MAT ファイル sldemo_hydcyl_data.mat から読み込んだデータを使用しています。パラメーターの値は Pump マスクと Cylinder マスクから変更できます。

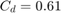
$$ C_d = 0.61 $$

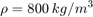
$$ \rho = 800\,kg/m^3 $$

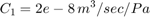
$$ C_1 = 2e-8\,m^3/sec/Pa $$

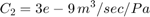
$$ C_2 = 3e-9\,m^3/sec/Pa $$

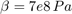
$$ \beta = 7e8\,Pa $$

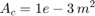
$$ A_c = 1e-3\,m^2 $$

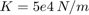
$$ K = 5e4\,N/m $$

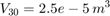
$$ V_{30} = 2.5e-5\,m^3 $$

T = [0 0.04 0.04 0.05 0.05 0.1 ] sec

Q = [0.005 0.005 0 0 0.005 0.005] (m^3)/sec

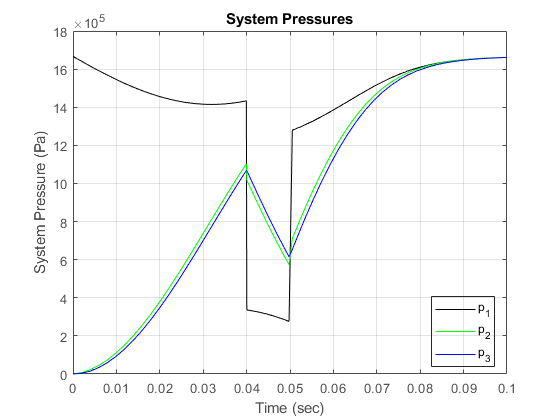
シミュレーション結果のプロット

ポンプ流量は最初に 0.005 m^3/sec = 300 l/min になり、t=0.04 sec でゼロになった後、t=0.05 sec で最初の流量に戻ります。

制御バルブは、ゼロのオリフィス面積から始まり、0.1 秒のシミュレーション時間中に 1e-4 m^2 へと一定の割合で増加します。バルブが閉じられると、ポンプ流量はすべて漏れるため、初期ポンプ圧は p10 = Q/C2 = 1667 kPa に上昇します。

バルブが開くと、圧力 p2 および p3 は上昇しますが、p1 は負荷増加に反応して低下します。ポンプ流量が途切れると、バネとピストンがアキュムレーターのような働きをし、p3 は低下し続けます。次に、流れが逆向きになるため、p2 は p3 に比較的近いものの低下します。ポンプ本体では、逆流量がすべて漏れ、p1 が低下します。流れが元に戻ると、これとは逆のことが起こります。

ピストン位置は p3 に正比例し、ここで油圧力とバネの力は釣り合っています。0.04 秒と 0.05 秒での速度の不連続性は、質量が無視できることを示しています。すべてのポンプ流量が再び漏れるようになると、制御バルブ全体で圧力降下がゼロになり、p3 = p2 = p1 = p10 となるため、モデルは安定状態に達します。

参考

トピック