直列 RLC 回路のモデル化

R2026a

モデルを開く

物理的なシステムは、陰的な形式の一連の微分方程式 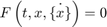$F\left(t,x,\dot{x} \right)=0$ 、または陰的な状態空間形式 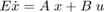$E\dot{x} =A\;x+B\;u\;$ として記述することができます。

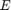が特異でない場合、このシステムは簡単に連立常微分方程式 (ODE) に変換して、ODE として解くことができます。

$\dot{x} =E^{-1} A x+E^{-1} B u$

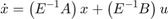
多くの場合、システムの状態はその導関数とは直接的な関係がないように見え、通常は物理的な保存則を表します。以下に例を示します。

$\begin{array}{l}\dot{x}_1 =x_2 \\0\;=x_1 +x_2 \end{array}$

この場合、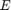は特異であり、逆行列は計算できません。一般的に、このクラスのシステムは "記述子" システムと呼ばれ、方程式は微分代数方程式 (DAE) と呼ばれます。

直列 RLC 回路

次のような簡単な直列 RLC 回路があるとします。

キルヒホフの電圧則によると、この回路の電圧低下は、各素子の電圧低下の合計と同じです。

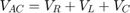
$V_{AC} = V_R+V_L+V_C$

キルヒホフの電流則により、次が成り立ちます。

$I_{AC}=I_R=I_L=I_C$

ここで、添字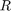、、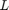および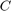はそれぞれ抵抗、インダクタンス、静電容量を表します。

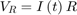
$V_{R} =I\left(t\right)R$

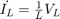
$V_L =L\dot{I}_L $ or $\dot{I}_L = \frac{1}{L}V_L$

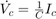
$V_C =V_{AC} \left(0\right)+\int_0^t I_C \left(\tau \right)d\tau$ または $\dot{V}_c =\frac{1}{C}I_c$

陰的な状態空間形式の記述

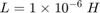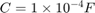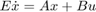$R=10\;\Omega$ 、 $L=1\times {10}^{-6} \;H$ 、 $C=1\times {10}^{-4} F$ でこのシステムを Simulink® でモデル化し、抵抗にかかる電圧を求めます。Descriptor State-Space ブロックを使用するために、システムは次に示すような、陰的な (すなわち "記述子の") 状態空間形式 $E\dot{x}=Ax+Bu$ で記述できます。

$\left\lbrack \begin{array}{ccccc}1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0\\0
& 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0\end{array}\right\rbrack
\left\lbrack \begin{array}{c}\dot{V}_C \\\dot{V}_L \\\dot{V}_R \\\dot{I}_L
\\\dot{I}_{AC} \end{array}\right\rbrack =\left\lbrack \begin{array}{ccccc}0
& 0 & 0 & \frac{1}{C} & 0\\1 & 1 & 1 & 0 & 0\\0 & 0 & -1 & R & 0\\0 & \frac{1}{L}
& 0 & 0 & 0\\0 & 0 & 0 & 1 & -1\end{array}\right\rbrack \left\lbrack \begin{array}{c}V_C
\\V_L \\V_R \\I_L \\I_{AC} \end{array}\right\rbrack +\left\lbrack \begin{array}{c}0\\-1\\0\\0\\0\end{array}\right\rbrack
V_{AC}$

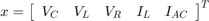ここで、 $x = {\left\lbrack \begin{array}{ccccc}V_C &V_L& V_R& I_L& I_{AC}\end{array}\right\rbrack}^T$ は状態ベクトルです。

抵抗にかかる電圧を測定しているため、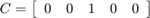 $C=\left\lbrack \begin{array}{ccccc}0&0& 1& 0&0\end{array}\right\rbrack$ に設定します。

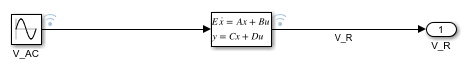
これを、代数ループによるシステムのモデル化でを求める場合と比較してください。

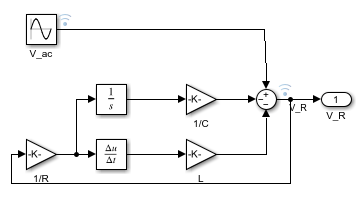
両方のモデルのシミュレーション結果は同じになります。しかし、Descriptor State-Space ブロックでは、ブロック線図がシンプルになり、代数ループを避けることができます。

参考

代数ループの概念

微分代数方程式のモデル化