MATLAB と Simulink での誘導システムの設計

この例では次を使用します。

この例では、ミサイル自動操縦設計に適用される高度な制御方法の使用に関する多くの出版物 (参照 [1]、[2]、[3]) で紹介されている、ミサイル機体のモデルの使用方法を示します。このモデルは、マッハ 2 ～ 4 の速度、高度 10,000 ft (3,050 m) ～ 60,000 ft (18,290 m)、典型的な迎え角度 +/-20°で飛行する尾翼制御ミサイルを表しています。

機体のダイナミクスのモデル

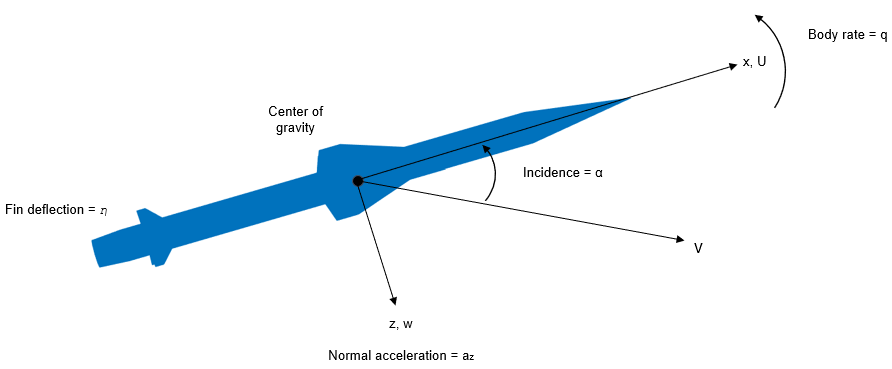
このモデルの核心要素は、機体の剛体ダイナミクスの非線形表現です。ミサイルのボディにかかる空気力およびモーメントは、入射角とマッハ数両方の非線形関数である係数から生成されます。このモデルは、Simulink® と Aerospace Blockset™ を使用して作成できます。このブロックセットの目的は、機体設定を問わずすべてのモデルに共通する、大気モデルなどの参照コンポーネントを提供することです。Aerospace Blockset で使用可能な簡略化バージョンのコンポーネントがこれらの例に含まれており、標準ブロックライブラリから再利用できることがわかります。

モデルを開きます。

Simulink での機体の表現

この機体モデルは、加速要求自動操縦を通じて制御される 4 つの主要サブシステムで構成されています。Atmosphere モデルでは、高度の変化に伴う大気の状態の変化が計算されます。Fin Actuator モデルと Sensors モデルでは、自動操縦が機体を結びつけて考えられます。Aerodynamics and Equations of Motion モデルでは、ミサイルのボディにかかる力およびモーメントの大きさが計算され、運動方程式が積分されます。

国際標準大気モデル

使用される Atmosphere Subsystem は国際標準大気に似ており、2 つの異なる領域に分かれています。対流圏領域は海抜 0 ～ 11 km にあります。この領域では、高度の上昇に伴って気温が直線的に下降すると仮定されます。対流圏領域の上にあるのが、海抜 11 ～ 20 km の下部成層圏領域です。この領域では、気温は一定であると仮定されます。

力とモーメントを作成するための空力係数

Aerodynamics and Equations of Motion Subsystem では、ミサイルのボディ軸にかかる力とモーメントが生成され、機体の線形運動および回転運動を定義する運動方程式が積分されます。

空力係数はデータセットに保存され、シミュレーション中、現在の操作条件における値は 2D ルックアップテーブルブロックを使用した内挿によって決定されます。

標準的な 3 ループ自動操縦設計

ミサイルを自動操縦する目的は、ミサイルのボディへの法線加速度を制御することです。この例での自動操縦構造は、重心の前に置かれた加速度計と追加減衰を提供するレートジャイロからの測定値を使用した、3 ループ設計です。コントローラーゲインは入射角とマッハ数でスケジュールされ、高度 10,000 ft でロバスト性能が得られるように調整されます。

標準的な設計法で自動操縦を設計するには、機体のピッチのダイナミクスの線形モデルを、平衡化した多くの飛行条件に関して導き出す必要があります。MATLAB® では、平衡化条件を決定し、線形状態空間モデルを非線形 Simulink モデルから直接導き出すことができるため、時間を節約でき、作成したモデルの検証にも役立ちます。MATLAB Control System Toolbox™ と Simulink® Control Design™ で提供されている関数を使用することにより、機体の開ループ周波数 (または時間) 応答の動作を可視化できます。機体モデルの平衡化および線形化の方法を確認するために、付属例「機体の平衡化と線形化」を実行できます。

機体の周波数応答

自動操縦は、予想される飛行エンベロープにおいてさまざまな飛行条件で導き出された多くの線形機体モデルに基づいて設計されます。非線形モデルでの自動操縦の実装には、オートパイロットゲインを 2 次元ルックアップテーブルで保存することや、フィン要求角が最大値を超えた場合の積分器のワインドアップを防ぐためにアンチワインドアップゲインを組み込むことなどが含まれます。非線形 Simulink モデルでの自動操縦のテストは、アクチュエータフィンやレート制限といった非線形性の存在下で、また飛行条件の変化に伴ってゲインが動的に変動する中で、申し分のない性能を示す最良の方法です。

図: ゲインスケジューリングされた自動操縦の Simulink 実装

Homing Guidance Loop

Homing Guidance Loop 一式は、ミサイルとターゲットの間の相対的な運動の測定値を返す Seeker/Tracker Subsystem と、自動操縦に渡される法線加速度の要求を生成する Guidance Subsystem で構成されています。自動操縦は、ホーミング誘導システム全体における内部ループの一部となっています。参照 [4] では、現在使用されている誘導のさまざまな形態や、誘導ループ性能の定量化に使用される解析手法の背景について説明しています。

Guidance Subsystem

Guidance Subsystem の役割は、閉ループトラッキング中に要求を生成するだけではなく、初期探索でターゲットの位置を突き止めることもあります。Stateflow® モデルは、このようなさまざまな操作モードの切り替えを制御するために使用されます。モード間の切り替えは、Simulink 内で生成されるイベントまたは Stateflow モデル内部のイベントによってトリガーされます。そして、Simulink に渡される変数 Mode の値を変更することにより、Simulink モデルの動作が制御されます。この変数は、生成可能な制御要求の切り替えに使用されます。ターゲットの探索中、Stateflow モデルでは、シーカーのジンバルに要求を送信することによって (Sigma) トラッカーが直接制御されます。ターゲットがシーカーのビーム幅の中に入ると、ターゲット捕そくのフラグが設定され (Acquire)、少し遅れて閉ループ誘導が開始されます。Stateflow は、すべての動作モード (正常動作であれ異常な状況であれ) を素早く定義できる理想的なツールです。たとえば、ターゲットが自動追跡されていない場合、つまりターゲット探索中にターゲットが取得されない場合にとられるべき動作が、この Stateflow ブロック線図で作成されます。

比例航法誘導

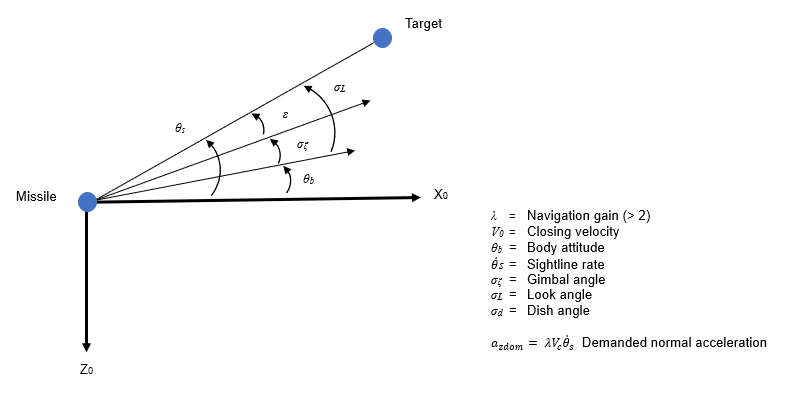
ターゲットが取得されると、ミサイルは衝突するまで比例航法誘導 (PNG) 則で誘導されます。この形式の誘導則は 1950 年代から誘導ミサイルに使用されてきましたが、現在では、レーダー誘導ミサイルや赤外線誘導ミサイル、テレビジョン誘導ミサイルに適用可能です。航法則では、ミサイルとターゲットとの閉成速度の測定値 (レーダー誘導ミサイルの場合はドップラー追跡装置を使用して取得可能) と、慣性視線角度の変化率推定が必要です。

図: 比例航法誘導則

Seeker/Tracker Subsystem

Seeker/Tracker Subsystem の目的は、シーカーのジンバルを駆動してシーカーの皿型アンテナをターゲットに合わせることと、誘導則に視線率の推定値を提供することです。トラッカーのループ時定数 tors は 0.05 秒に設定され、応答速度を最大限にすることと騒音伝達を許容レベル以下に維持することとの妥協点として選択されます。照準収束ループはボディ回転率を補うことを目標としており、ゲイン Ks (ループの交差周波数) は、照準収束速度ジャイロの帯域幅制限のもとで、できるだけ高く設定されます。視線率の推定値は、照準収束速度ジャイロで測定された皿型アンテナの角度の変化率と、受信機で測定された角度追跡誤差 (e) の変化率の推定値を合計してフィルター処理した値です。この例では、推定器フィルターの帯域幅を自動操縦の帯域幅の半分に設定しています。

レードーム逸脱

レーダー誘導ミサイルの場合、一般的にモデル化される寄生フィードバックの影響は、レードーム逸脱の影響です。レードーム逸脱が発生するのは、返ってきた信号がシーカーの保護被覆の形状によってゆがめられ、ターゲットに対するルックアングルが誤って読み取られるためです。一般的に、ゆがみの量は現在のジンバル角度の非線形関数ですが、これに類似するものとして一般的に使用されているのは、ジンバル角度とゆがみの大きさの線形関係を仮定することです。上記のシステムでは、レードーム逸脱は、"Radome Aberration" というラベルの付いた Gain ブロックで説明されます。その他の寄生効果 (法線加速度に対するレートジャイロの感度など) も、ターゲットトラッカーと推定器フィルターのロバスト性をテストする目的で、しばしばモデル化されます。

図: レードーム逸脱の形状

誘導シミュレーションの実行

次に、システム全体の性能を示します。この場合、ターゲットはミサイルの初期位置よりも 500 m 上空を、ミサイルの初期機首方位を逆進しながら一定速度 328 m/s で飛行すると定義されています。シミュレーション結果から、捕そくは結合から 0.69 秒後で、閉ループ誘導は 0.89 秒に開始されたと判断できます。ターゲットとの衝突は 3.46 秒後で、最接近地点での距離は 0.265 m と計算されました。

aero_guid_plot.m スクリプトによる性能解析の作成

アニメーションブロックによるシミュレーションの視覚的参照

参照

1. "Robust LPV control with bounded parameter rates", S.Bennani, D.M.C. Willemsen, C.W. Scherer, AIAA-97-3641, August 1997.

2. "Full Envelope Missile Longitudinal Autopilot Design using the State-Dependent Riccati Equation Method", C.P.Mracek and J.R. Cloutier, AIAA-97-3767, August 1997.

3. "Gain-Scheduled Missile Autopilot Design Using Linear Parameter Varying Transformations", J.S.Shamma, J.R. Cloutier, Journal of Guidance, Control and Dynamics, Vol. 16, No. 2, March-April 1993.

4. "Modern Navigation, Guidance, and Control Processing Volume 2", Ching-Fang Lin, ISBN 0-13-596230-7, Prentice Hall, 1991.