高速ダイナミクスの削減
高速ダイナミクスは計算時間に大きな影響を及ぼす可能性があります。ソルバーでスティッフな振動やウォーター ハンマーなどの急速に発生するイベントが検出された場合、各イベントを計算するために実行するステップを小さくする必要があります。高速ダイナミクスを削減すると、ソルバーがより大きなステップを実行できるようになり、モデルがリアルタイム対応になる可能性が高くなります。周波数応答解析および極解析を使用して、システムのダイナミクスを解析できます。
周波数応答解析
"周波数応答" は、正弦波入力に対するシステムの定常状態応答を表します。線形システムの場合、正弦波入力は、周波数 ω が同じで振幅と位相 θ の異なる正弦波を出力します。

周波数解析は、与えられた周波数の範囲で振幅と位相がどのように変化するかを示します。小さな周波数の変化で振幅または位相が大きく変化するのは、システムに高速ダイナミクスがあることを示しています。図では、振幅 (dB 単位の振幅) と位相が周波数の関数としてどのように変化するかを見ることができるボード線図を使用しています。
極解析
高速極も、高速ダイナミクスがあることを示します。高速極は高速で応答または発振する極です。複素平面上で虚軸から左に離れた実数部をもつ極の応答速度は速くなります。実軸から離れた虚数部をもつ複素共役極対は高速で発振します。たとえば、-1500 の実極は -1000 の実極より応答速度が速く、-500 ± 1500i の複素共役極対は -500 ± 500i の複素共役極対より発振速度が速くなります。
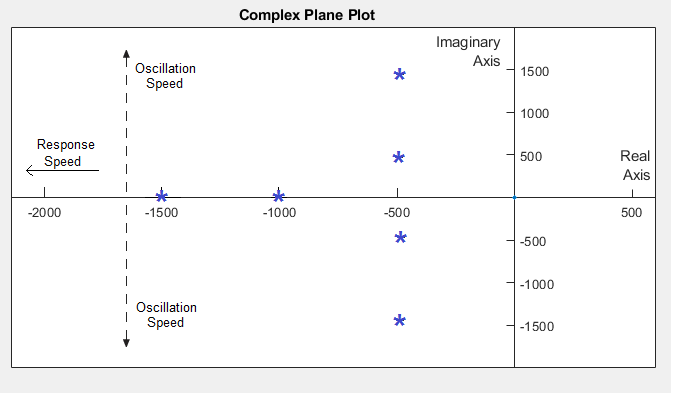
状態空間モデルでは、極は A 行列の固有値です。この例では、状態空間モデルを決定してから A 行列値の固有値を計算しプロットすることによって極の速度を調べる方法を説明します。