信号のパワーの測定
信号のパワーは時間領域サンプルの絶対値二乗和を信号長で除算したもので、RMS レベルの二乗と等価です。関数 bandpower を使用すると、信号のパワーを一度に推定できます。
ホワイト ガウス ノイズに含まれる、1 kHz で 1.2 秒間サンプリングされたユニット チャープについて考えます。チャープの周波数は、1 秒間で初期値の 100 Hz から 300 Hz に増加します。ノイズの分散は です。再現可能な結果が必要な場合は、乱数発生器をリセットします。
N = 1200;
Fs = 1000;
t = (0:N-1)/Fs;
sigma = 0.01;
rng('default')
s = chirp(t,100,1,300)+sigma*randn(size(t));bandpower で与えられるパワー推定は定義と等価であることを確認します。
pRMS = rms(s)^2
pRMS = 0.5003
powbp = bandpower(s,Fs,[0 Fs/2])
powbp = 0.5005
obw を使用して、信号のパワーの 99% を含む周波数帯域の幅、帯域の下限と上限および帯域のパワーを推定します。この関数は、スペクトル推定もプロットし、占有帯域幅に注釈を付けます。
obw(s,Fs);
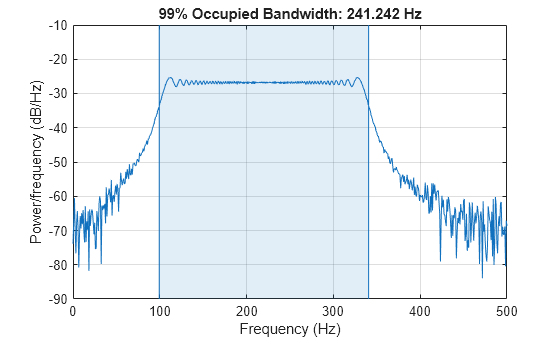
[wd,lo,hi,power] = obw(s,Fs); powtot = power/0.99
powtot = 0.5003
非線形パワー増幅器が 60 Hz の正弦波を入力として与えられ、3 次の歪みをもつノイズを含んだ信号を出力します。信号は 3.6 kHz で 2 秒間サンプリングされます。
Fs = 3600; t = 0:1/Fs:2-1/Fs; x = sin(2*pi*60*t); y = polyval(ones(1,4),x) + randn(size(x));
増幅器は 3 次の歪みを生じるため、出力信号は以下をもつことが予想されます。
入力と同じ 60 Hz の周波数をもつ "基本波" 成分。
2 つの "高調波" — 入力の 2 倍および 3 倍の 120 Hz および 180 Hz の周波数をもつ周波数成分。
関数 thd を使用して、信号のスペクトルを可視化します。基本波および高調波に注釈を付けます。
thd(y,Fs);

関数 bandpower を使用して、基本成分と高調波に蓄積されているパワーを求めます。各値は合計パワーに対するパーセントとデシベルで表されます。値は表形式で表示されます。
pwrTot = bandpower(y,Fs,[0 Fs/2]);
Harmonic = {'Fundamental';'First';'Second'};
Freqs = [60 120 180]';
Power = zeros([3 1]);
for k = 1:3
Power(k) = bandpower(y,Fs,Freqs(k)+[-10 10]);
end
Percent = Power/pwrTot*100;
inDB = pow2db(Power);
T = table(Freqs,Power,Percent,inDB,'RowNames',Harmonic)T=3×4 table
Freqs Power Percent inDB
_____ _______ _______ _______
Fundamental 60 1.5777 31.788 1.9804
First 120 0.13141 2.6476 -8.8137
Second 180 0.04672 0.9413 -13.305
参考
bandpower | pow2db | pwelch | snr