ダウンサンプリングを使用した信号の位相の取得

この例では、downsample を使用して、信号の "位相" を求める方法を示します。信号を M でダウンサンプリングすると M 個の固有の位相が生じます。たとえば、離散時間信号 $\mathit{x}$ がある場合 (ここで、$\mathit{x}\left(0\right),\mathit{x}\left(1\right),\mathit{x}\left(2\right),\mathit{x}\left(3\right),...,\mathit{x}\left(\mathit{n}-1\right)$)、x の M 個の位相は、$\mathit{x}\left(\mathrm{nM}+\mathit{k}\right)$ になります (ここで、$\mathit{k}=0,1,...,\mathit{M}-1$)。

$\mathit{M}$ 個の信号は x の "ポリフェーズ" 成分と呼ばれます。

ホワイト ノイズ ベクトルを作成して、3 によるダウンサンプリングに関連付けられた 3 つのポリフェーズ成分を求めます。

再現性のある結果が得られるように、乱数発生器を既定の設定にリセットします。ホワイト ノイズ ランダム ベクトルを生成して、3 によるダウンサンプリングに関連付けられた 3 つのポリフェーズ成分を求めます。

rng("default")
x = randn(36,1);
x0 = downsample(x,3,0);
x1 = downsample(x,3,1);
x2 = downsample(x,3,2);

ポリフェーズ成分は元の信号の 1/3 の長さをもちます。

upsample を使用して、ポリフェーズ成分の 3 によるアップサンプリングを行います。

y0 = upsample(x0,3,0);
y1 = upsample(x1,3,1);
y2 = upsample(x2,3,2);

結果をプロットします。

tiledlayout("vertical")
nexttile
stem(x,Marker="none")
title("Original Signal")
ylim([-4 4])

nexttile
stem(y0,Marker="none")
ylabel("Phase 0")
ylim([-4 4])

nexttile
stem(y1,Marker="none")
ylabel("Phase 1")
ylim([-4 4])

nexttile
stem(y2,Marker="none")
ylabel("Phase 2")
ylim([-4 4])

アップサンプリングしたポリフェーズ成分の和を求めると元の信号が得られます。

離散時間正弦波を作成して、2 によるダウンサンプリングに関係する 2 つのポリフェーズ成分を求めます。

$$\pi /4$$ ラジアン/サンプルの角周波数で離散時間正弦波を作成します。正弦波に 2 の DC オフセットを加算してポリフェーズ成分の可視化に役立てます。正弦波を 2 によるダウンサンプリングして、偶数と奇数のポリフェーズ成分を求めます。

n = 0:127;
x = 2+cos(pi/4*n);
x0 = downsample(x,2,0);
x1 = downsample(x,2,1);

2 つのポリフェーズ成分をアップサンプリングします。

y0 = upsample(x0,2,0);
y1 = upsample(x1,2,1);

比較のため、アップサンプリングしたポリフェーズ成分を元の信号とともにプロットします。

tiledlayout("vertical")
nexttile
stem(x,Marker="none")
ylim([0.5 3.5])
title("Original Signal")
nexttile
stem(y0,Marker="none")
ylim([0.5 3.5])
ylabel("Phase 0")
nexttile
stem(y1,Marker="none")
ylim([0.5 3.5])
ylabel("Phase 1")

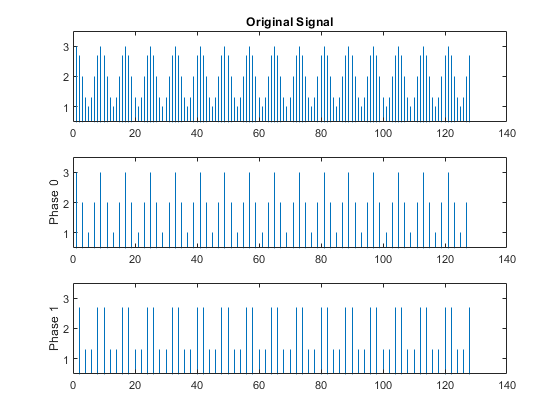
アップサンプリングした 2 つのポリフェーズ成分 (位相 0 と位相 1) の和を求めると元の正弦波が得られます。

参考

downsample | upsample