このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

ディリクレ関数

関数 diric では、"周期的 sinc" 関数または "エイリアス sinc" 関数とも呼ばれるディリクレ関数を、入力ベクトルや入力行列 x に対して計算します。ディリクレ関数は以下によって定義されます。

$$D(x)=\{\begin{array}{cc}{\displaystyle \frac{\sin (Nx/2)}{{\displaystyle N\sin (x/2)}}},& x\ne 2\pi k\text{,}\\ (-1{)}^{k(N-1)},& x=2\pi k\text{,}\end{array}k=0,\pm 1,\pm 2,\pm 3,\dots$$

ここで、$$N$$ はユーザーが指定する正の整数です。ディリクレ関数の周期は、奇数値の $$N$$ に対しては $$2\pi$$、偶数値の $$N$$ に対しては $$4\pi$$ となります。この関数の振幅は、$$N$$ 点箱型ウィンドウでの離散時間フーリエ変換の振幅の $$1/N$$ 倍です。

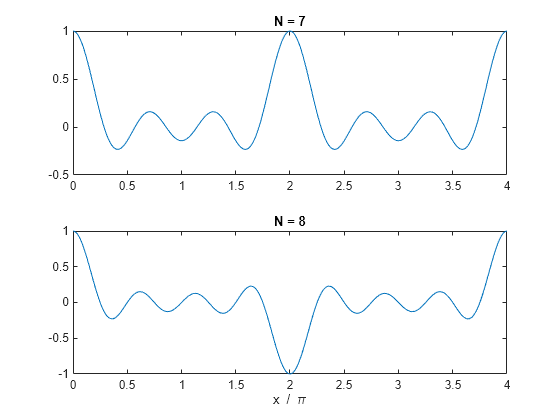
$$N=7$$ および $$N=8$$ について 0 ～ $$4\pi$$ の区間でディリクレ関数をプロットするには、以下を使用します。

x = linspace(0,4*pi,300);

subplot(2,1,1)
plot(x/pi,diric(x,7))
title('N = 7')

subplot(2,1,2)
plot(x/pi,diric(x,8))
title('N = 8')
xlabel('x / \pi')

参考

diric | sinc