azel2phitheta
Convert angles from azimuth-elevation form to phi-theta form
Description
PhiTheta = azel2phitheta(AzEl)
Examples
Find the phi-theta representation for 30° azimuth and 10° elevation for the convention where phi is defined from the y-axis to the z-axis, and theta is defined from the x-axis toward the yz-plane.
PhiTheta = azel2phitheta([30;10])
PhiTheta = 2×1
19.4254
31.4749
Find the phi-theta representation for 30° azimuth and 10° elevation for the convention with phi defined from the x-axis to the y-axis, and theta defined from the z-axis toward the xy-plane.
PhiTheta = azel2phitheta([30;10],false)
PhiTheta = 2×1
30.0000
80.0000
Input Arguments
Azimuth and elevation angles, specified as a two-row matrix. Each column of the matrix represents an angle in degrees, in the form [azimuth; elevation].
Data Types: double
Phi-theta angle convention selection, specified as true
or false.
If
RotAxistrue, the phi angle is defined from the y-axis to the z-axis and the theta angle is defined from the x-axis toward the yz-plane.If
RotAxisfalse, the phi angle is defined from the x-axis to the y-axis and the theta angle is defined from the z-axis toward the xy- plane. (see Alternative Definition of Phi and Theta).
Data Types: double
Output Arguments
Phi and theta angles, returned as a two-row matrix. Each column of the
matrix represents an angle in degrees, in the form [phi; theta]. The matrix
dimensions of PhiTheta are the same as those of
AzEl.
More About
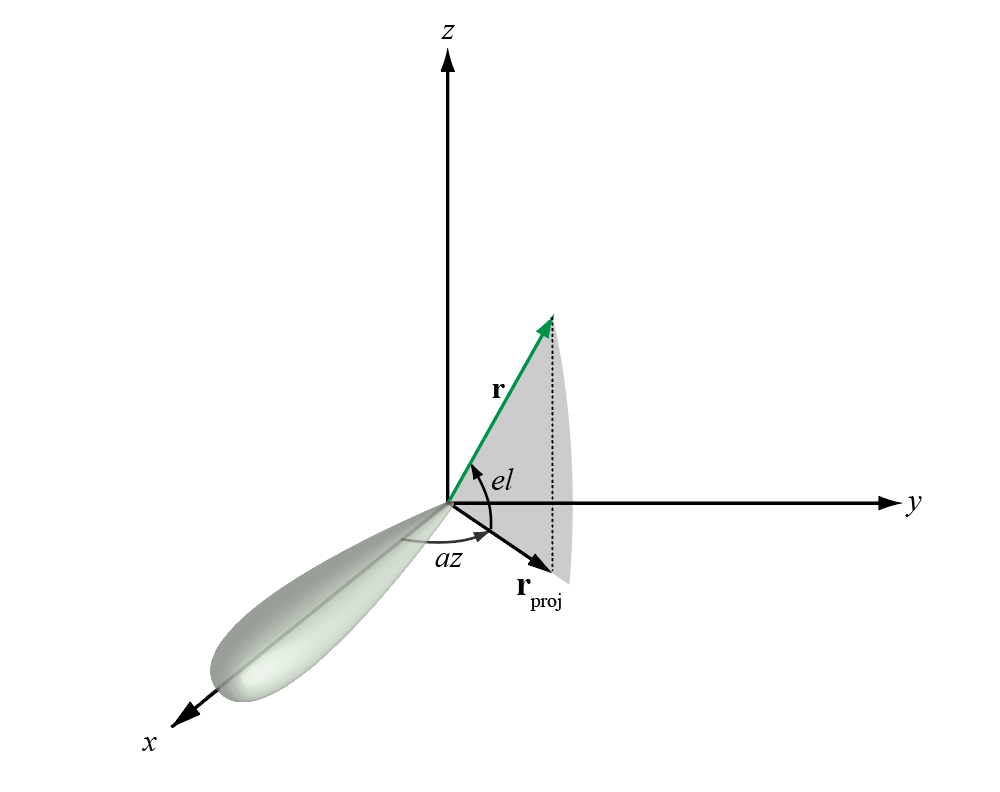
The azimuth angle of a vector is the angle between the x-axis and the orthogonal projection of the vector onto the xy plane. The angle is positive in going from the x axis toward the y axis. Azimuth angles lie between –180 and 180 degrees. The elevation angle is the angle between the vector and its orthogonal projection onto the xy-plane. The angle is positive when going toward the positive z-axis from the xy plane. By default, the boresight direction of an element or array is aligned with the positive x-axis. The boresight direction is the direction of the main lobe of an element or array.
Note
The elevation angle is sometimes defined in the literature as the angle a vector makes with the positive z-axis. The MATLAB® and Phased Array System Toolbox™ products do not use this definition.
This figure illustrates the azimuth angle and elevation angle for a vector shown as a green solid line.
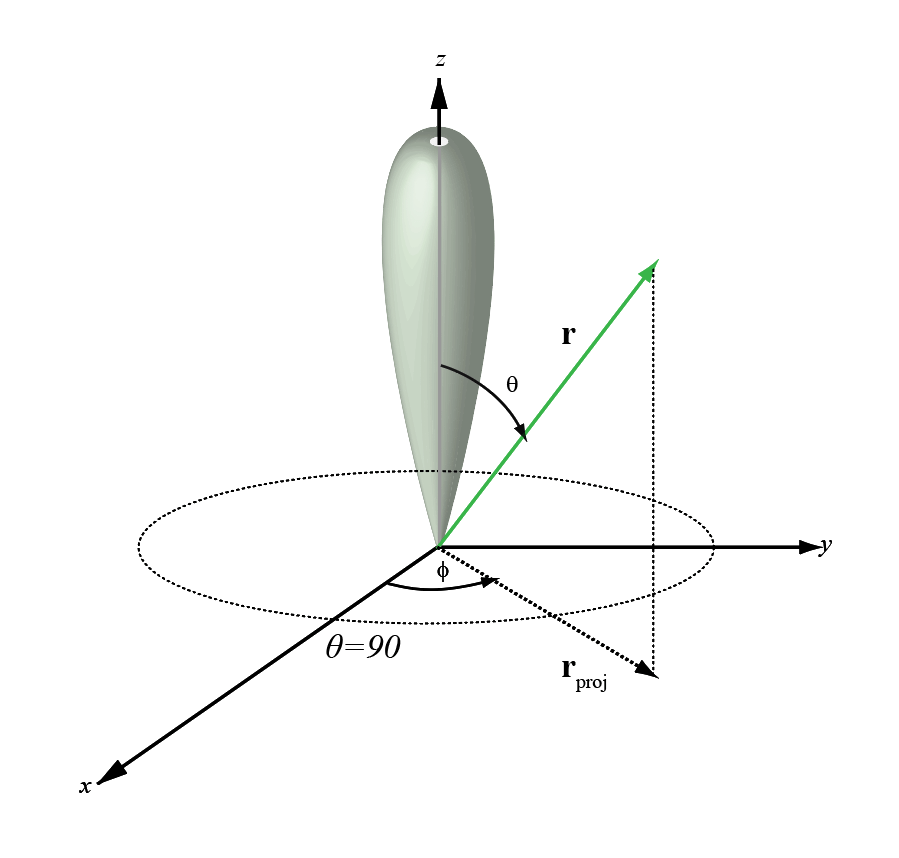
The phi angle (φ) is the angle from the positive y-axis to the vector’s orthogonal projection onto the yz plane. The angle is positive toward the positive z-axis. The phi angle is between 0 and 360 degrees. The theta angle (θ) is the angle from the x-axis to the vector itself. The angle is positive toward the yz plane. The theta angle is between 0 and 180 degrees.
The figure illustrates phi and theta for a vector that appears as a green solid line.

The coordinate transformations between φ/θ and az/el are described by the following equations
This transformation applies when RotAx is
true.
The phi angle (φ) is the angle from the positive x-axis to the vector’s orthogonal projection onto the xy plane. The angle is positive toward the positive y-axis. The phi angle is between 0 and 360 degrees. The theta angle (θ) is the angle from the z-axis to the vector itself. The angle is positive toward the xy plane. The theta angle is between 0 and 180 degrees.
The figure illustrates φ and θ for a vector that appears as a green solid line.
Extended Capabilities
Usage notes and limitations:
Does not support variable-size inputs.
Version History
Introduced in R2012a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)