fegeometry
Description
An fegeometry object contains a geometry for use
in a finite element analysis with an femodel
object.
Creation
Syntax
Description
gm = fegeometry(geometry,Name=Value)fegeometry object using one or more name-value arguments.
For this syntax, geometry must specify a path to an STL or STEP
file.
gm = fegeometry(nodes,elements,ElementIDToRegionID)ElementIDToRegionID specifies the
domain IDs for each element of the mesh.
Input Arguments
geometry — Geometry description
string scalar | character vector | decomposed geometry matrix | handle to a geometry function | triangulation object | delaunayTriangulation object | DiscreteGeometry object | AnalyticGeometry object
Geometry description, specified as one of these values:
String scalar or character vector that contains a path to an STL or STEP file. The path must end with the file extension
".stl",".STL",".stp",".STP",".step",".STEP", or any combination of uppercase and lowercase letters in this extension.Decomposed geometry matrix or a handle to a geometry function. For details about a decomposed geometry matrix, see
decsg. A geometry function must return the same result for the same input arguments in every function call. Thus, it must not contain functions and expressions designed to return a variety of results, such as random number generators.triangulationobject. Thefegeometryfunction accepts both surface triangulation and triangulation with tetrahedra for 3-D geometries. For a 3-D geometry created from surface triangulation, theMeshproperty remains empty. For a 2-D geometry or a 3-D geometry created from triangulation with tetrahedra,fegeometryuses triangulation points and connectivity list to specify a linear mesh. If theMeshproperty is empty or your task requires a more accurate quadratic mesh or a finer linear mesh, use thegenerateMeshfunction.delaunayTriangulationobject. Thefegeometryfunction uses triangulation points to specify a mesh. If your task requires a more accurate quadratic mesh, use thegenerateMeshfunction.DiscreteGeometryobject.AnalyticGeometryobject.
nodes — Mesh nodes
Nnodes-by-2 numeric matrix | Nnodes-by-3 numeric matrix
Mesh nodes, specified as an Nnodes-by-2 or
Nnodes-by-3 matrix for a 2-D or 3-D geometry,
respectively. Nnodes is the number of nodes in the mesh. Each row
of the matrix contains x-, y-, and, if
applicable, z- coordinates of one node.
Data Types: double
elements — Mesh elements
Nelements-by-3 integer matrix | Nelements-by-4 integer matrix | Nelements-by-6 integer matrix | Nelements-by-10 integer matrix
Mesh elements, specified as an integer matrix with Nelements
rows and 3, 4, 6, or 10 columns, where Nelements is the number of
elements in the mesh.
Linear planar mesh or linear mesh on the geometry surface has size
Nelements-by-3. Each row ofelementscontains the indices of the triangle corner nodes for a surface element. In this case, the resulting geometry does not contain a full mesh. Create the mesh using thegenerateMeshfunction.Linear elements have size
Nelements-by-4. Each row ofelementscontains the indices of the tetrahedral corner nodes for an element.Quadratic planar mesh or quadratic mesh on the geometry surface has size
Nelements-by-6. Each row ofelementscontains the indices of the triangle corner nodes and edge centers for a surface element. In this case, the resulting geometry does not contain a full mesh. Create the mesh using thegenerateMeshfunction.Quadratic elements have size
Nelements-by-10. Each row ofelementscontains the indices of the tetrahedral corner nodes and the tetrahedral edge midpoint nodes for an element.
For details on node numbering for linear and quadratic elements, see Mesh Data.
Data Types: double
ElementIDToRegionID — Domain information for each mesh element
vector of positive integers
Domain information for each mesh element, specified as a vector of positive integers. Each mesh element is an ID of a geometric region for an element of the mesh. The length of this vector equals the number of elements in the mesh.
Data Types: double
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: gm = fegeometry("AngleBlock.step",MaxRelativeDeviation=5)
imports a geometry from the AngleBlock.step file using the relative sag
of 5.
AllowSelfIntersections — Indicator to allow import of self-intersecting geometry
true or 1 (default) | false or 0
Since R2024a
Indicator to allow the import of a self-intersecting geometry from an STL or
STEP file, specified as true or false. You
also can use 1 or 0 instead of
true or false. By default,
fegeometry does not check for self-intersections and lets you
import these types of geometries. If you set this argument to
false or 0, fegeometry
issues an error for a geometry with self-intersections.
Example: AllowSelfIntersections=true
FeatureAngle — Threshold for dihedral angle between adjacent triangles
44 (default) | number between 10 and 90
Since R2024a
Threshold for the dihedral angle between adjacent triangles to indicate the edge
and create two separate faces, specified as a number between 10 and 90. The
specified FeatureAngle value represents degrees. This argument
works only for importing a geometry from an STL file.
If the angle between the triangles exceeds the threshold, the edge becomes a
topological (feature) edge separating two faces. If the angle does not exceed the
threshold, fegeometry does not create a topological edge with two
separate faces, unless the function can create the edge based on other criteria.
Instead, fegeometry creates one face.
Example: FeatureAngle=30
MaxRelativeDeviation — Relative sag
1 (default) | number in the range [0.1, 10]
Relative sag for importing a STEP geometry, specified as a number in the range
[0.1,10]. This value controls the accuracy of the geometry
import from a STEP file. A relative sag is the ratio between the local absolute sag
and the local mesh edge length. The absolute sag is the maximal gap between the mesh
and the geometry.

Example: MaxRelativeDeviation=5
Data Types: double
Properties
NumCells — Number of geometry cells
nonnegative integer
This property is read-only.
Number of geometry cells, returned as a nonnegative integer.
Data Types: double
NumFaces — Number of geometry faces
positive integer
This property is read-only.
Number of geometry faces, returned as a positive integer.
Data Types: double
NumEdges — Number of geometry edges
nonnegative integer
This property is read-only.
Number of geometry edges, returned as a nonnegative integer.
Data Types: double
NumVertices — Number of geometry vertices
nonnegative integer
This property is read-only.
Number of geometry vertices, returned as a nonnegative integer.
Data Types: double
Vertices — Coordinates of geometry vertices
N-by-2 numeric matrix | N-by-3 numeric matrix
This property is read-only.
Coordinates of geometry vertices, returned as an
N-by-2 or
N-by-3 numeric matrix for a 2-D or 3-D geometry,
respectively. Here, N is the number of vertices.
Data Types: double
Mesh — Mesh for solution
FEMesh object
Mesh for solution, specified as an FEMesh object. See FEMesh Properties for details.
Object Functions
addCell | Combine two geometries by adding one inside a cell of another |
addFace | Fill void regions in 2-D and split cells in 3-D geometry |
addVertex | Add vertex on geometry boundary |
addVoid | Create void regions inside 3-D geometry |
cellEdges | Find edges belonging to boundaries of specified cells |
cellFaces | Find faces belonging to specified cells |
extrude | Vertically extrude 2-D geometry or specified faces of 3-D geometry |
faceEdges | Find edges belonging to specified faces |
facesAttachedToEdges | Find faces attached to specified edges |
generateMesh | Create triangular or tetrahedral mesh |
mergeCells | Merge geometry cells |
nearestEdge | Find edges nearest to specified point |
nearestFace | Find faces nearest to specified point |
pdegplot | Plot PDE geometry |
pdemesh | Plot PDE mesh |
rotate | Rotate geometry |
scale | Scale geometry |
translate | Translate geometry |
triangulation | Create triangulation object from
fegeometry |
Examples
fegeometry Object from DiscreteGeometry Object
Create an fegeometry object from a DiscreteGeometry object by assigning it to an femodel object for a finite element analysis.
Create and plot a 3-D geometry consisting of three nested cuboids of the same height.
gm = multicuboid([2 3 5],[4 6 10],3);
pdegplot(gm,CellLabels="on",FaceAlpha=0.3)
Create an femodel object for solving a static structural problem and assign the geometry to the model.
model = femodel(AnalysisType="structuralStatic", ... Geometry=gm); model.Geometry
ans =
fegeometry with properties:
NumFaces: 18
NumEdges: 36
NumVertices: 24
NumCells: 3
Vertices: [24x3 double]
Mesh: []
fegeometry Object from STL File
Create an fegeometry object from an STL file representing a forearm link, and use it for a finite element analysis with an femodel object.
Create an femodel object for solving a static structural problem, and assign the geometry to the model.
model = femodel(AnalysisType="structuralStatic", ... Geometry="ForearmLink.stl"); model.Geometry
ans =
fegeometry with properties:
NumFaces: 147
NumEdges: 329
NumVertices: 213
NumCells: 1
Vertices: [213x3 double]
Mesh: []
Plot the geometry.
pdegplot(model,FaceAlpha=0.3)

fegeometry Object from Function Handle
Create an fegeometry object from a function handle.
gm = fegeometry(@cardg)
gm =
fegeometry with properties:
NumFaces: 1
NumEdges: 4
NumVertices: 4
NumCells: 0
Vertices: [4x2 double]
Mesh: []
Plot the geometry with the edge labels.
pdegplot(gm,EdgeLabels="on");
fegeometry Object from Geometry Description Matrix
Create an fegeometry object from a geometry description matrix.
g = [3 4 0 1 1 0 0 0 1.0 1.0]; sf = 'S1'; ns = 'S1'; gm = fegeometry(decsg(g',sf,ns'))
gm =
fegeometry with properties:
NumFaces: 1
NumEdges: 4
NumVertices: 4
NumCells: 0
Vertices: [4x2 double]
Mesh: []
Plot the geometry with the edge labels.
pdegplot(gm,EdgeLabels="on");
xlim([-0.1 1.1])
ylim([-0.1 1.1])
fegeometry Object from triangulation Object
Since R2023b
Create an fegeometry object from a 2-D triangulation object.
Define the points in a 2-D triangulation.
P = [2.5 8.0;
6.5 8.0;
2.5 5.0;
6.5 5.0;
1.0 6.5;
8.0 6.5];Define the triangulation connectivity list.
T = [5 3 1;
3 2 1;
3 4 2;
4 6 2];Create the triangulation representation.
TR = triangulation(T,P)
TR =
triangulation with properties:
Points: [6x2 double]
ConnectivityList: [4x3 double]
Create an fegeometry object from the triangulation object TR.
gm = fegeometry(TR)
gm =
fegeometry with properties:
NumFaces: 1
NumEdges: 6
NumVertices: 6
NumCells: 0
Vertices: [6x3 double]
Mesh: [1x1 FEMesh]
The created geometry includes a linear mesh.
gm.Mesh
ans =
FEMesh with properties:
Nodes: [2x6 double]
Elements: [3x4 double]
MaxElementSize: 5
MinElementSize: 2.1213
MeshGradation: []
GeometricOrder: 'linear'
To create a more accurate quadratic mesh, use generateMesh.
gm = generateMesh(gm); gm.Mesh
ans =
FEMesh with properties:
Nodes: [2x871 double]
Elements: [6x408 double]
MaxElementSize: 0.3046
MinElementSize: 0.1523
MeshGradation: 1.5000
GeometricOrder: 'quadratic'
Self-Intersecting Geometry
Since R2024a
Check for self-intersections while importing the geometry of a cover.
Create an fegeometry object from an STL file and plot the
geometry.
gm = fegeometry("Cover.stl");
pdegplot(gm)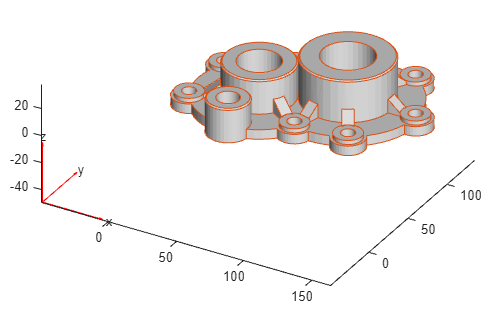
Create an femodel object for solving a static structural problem,
and assign the geometry to the model.
model = femodel(AnalysisType="structuralStatic", ... Geometry=gm);
Generate a mesh and assign the result to the model to update the mesh stored in the
Geometry property of the model. The mesh generator issues a warning
about poor quality of some of the mesh elements.
model = generateMesh(model);
Warning: Found elements with poor shape quality. (Type "warning off pde:pdeMeshGenerator:ElementQualityWarn" to suppress this warning.) > In pde.EquationModel/generateMesh (line 104) In fegeometry/generateMesh (line 220) In femodel/generateMesh (line 344)
Rotate the geometry plot to check for any problematic areas. By looking at the top of the geometry, you can see that three of the cylinders might be in contact with each other or intersecting each other.
figure pdegplot(gm) view([30 90])

Use the AllowSelfIntersections argument to check for
self-intersections while importing a geometry. If you set this argument to
false, fegeometry does not allow the import if a
geometry has self-intersections.
gm = fegeometry("Cover.stl",AllowSelfIntersections=false)Unable to import a self-intersecting geometry.
Version History
Introduced in R2023aR2024a: Import geometries using AllowSelfIntersections and FeatureAngle
When importing a geometry from a file, you can set the
AllowSelfIntersections name-value argument to check for self
intersecting geometries. You can also use the FeatureAngle name-value
argument to specify a threshold for the dihedral angle between adjacent triangles to
indicate the edge between separate faces.
Also, the fegeometry function now removes scratch edges when
importing a geometry from an STL or STEP file. Scratch edges are the edges with both ends
disconnected from the rest of the geometry edges.
R2023b: Create geometry from triangulation and delaunayTriangulation objects
You can use triangulation, specified as a triangulation or delaunayTriangulation object, to create an
fegeometry object.
See Also
Functions
generateMesh|pdegplot|addCell|addFace|addVertex|addVoid|rotate|scale|translate|extrude|cellEdges|cellFaces|faceEdges|facesAttachedToEdges|nearestEdge|nearestFace
Objects
MATLAB コマンド
次の MATLAB コマンドに対応するリンクがクリックされました。
コマンドを MATLAB コマンド ウィンドウに入力して実行してください。Web ブラウザーは MATLAB コマンドをサポートしていません。

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)