ValueStore によるモンテカルロ バッチ ジョブの監視

この例では、実行中にValueStoreを使用してモンテカルロ バッチ ジョブを監視する方法を示します。

すべてのジョブに、ジョブの実行中にデータにアクセスするために使用できる ValueStore オブジェクトが関連付けられています。ジョブの実行中もコマンド ラインの使用を継続できます。この例では、ValueStore オブジェクトを使用して、ジョブの実行中にバッチ モンテカルロ シミュレーションのデータにアクセスし、そのデータを監視する方法を示します。

モンテカルロによる π の推定

さまざまなモンテカルロ法を使用して π の値を推定できます。この例では、シンプルなモンテカルロ面積法で π を推定する方法を示します。

モンテカルロ面積法で π を推定するには、次の手順を実行します。

1. 一様分布から点の $\mathit{x}$ 座標と $\mathit{y}$ 座標をランダムに生成します。

2. 点が正方形に内接する円の内側にあるかどうかを判定します。円の内側にある点の数と点の総数を更新します。

3. 必要に応じて繰り返して推定を改良します。

詳細については、この例のシンプルなモンテカルロ面積法セクションを参照してください。

複数のシミュレーションを並列実行し、中間結果をジョブの ValueStore オブジェクトにキーと値のエントリとして格納します。補助関数 updatePlot を使用して、ValueStore オブジェクトから結果を取得して処理し、プロットを更新してシミュレーションの進行状況を監視します。

中間結果を可視化するプロットの準備

円の半径とジョブによる parfor ループの反復回数を指定します。

r = 1;
steps = 200; 

モンテカルロ シミュレーションの中間結果を可視化する 2 つのプロットを作成します。タイトル、ラベル、範囲などの設定を含めます。シミュレーション中に自動的に更新されるときに変わらないように座標軸の縦横比を設定します。

fig1 = figure(Name="Estimate Pi with Monte Carlo",Visible="on");
ax1 = gca(fig1);
theta = linspace(0,2*pi);
m = cos(theta);
n = sin(theta);
plot(ax1,m,n,"k")
xlabel(ax1,"Value of $x$",Interpreter="latex");
ylabel(ax1,"Value of $y$",Interpreter="latex");
title(ax1,"Randomly Generated Points in Circle",Interpreter="latex");

axis(ax1,"equal",[-1 1 -1 1]) 

fig2 = figure(Name="Current Pi Estimate",Visible="on");
ax2 = gca(fig2);
xlabel(ax2,"Steps",Interpreter="latex");
ylabel(ax2,"Estimate of $\pi$",Interpreter="latex");
title(ax2,"Current Estimate of $\pi$",Interpreter="latex");
xlim(ax2,([0 steps]))
ylim(ax2,([0 4])) 

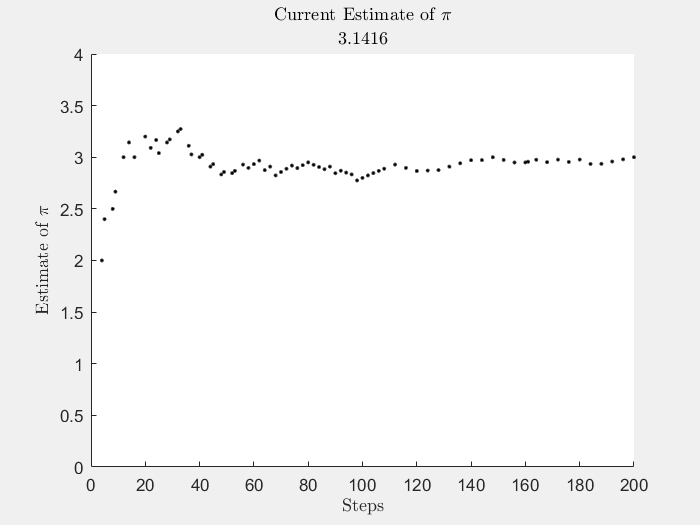
バッチ ジョブの設定と投入

既定のクラスター並列環境からクラスター オブジェクトを作成します。既定の並列環境を確認するには、MATLAB の [ホーム] タブの [環境] セクションで、[並列] をクリックして [並列環境を選択] をポイントします。

cluster = parcluster;

この例の最後で定義している関数 GeneratePoints に、モンテカルロ シミュレーションの定義が含まれています。batchを使用し、入力引数 r および steps を指定して GeneratePoints 内の計算をオフロードします。名前と値の引数 Pool を使用して 4 つのワーカーをもつ並列プールを作成します。関数 batch による関数の実行に別のワーカーが使用されるため、要求するプール ワーカーの数はクラスターで使用可能なワーカーの数よりも 1 つ少なくなることを確認してください。

job = batch(cluster,@generatePoints,1,{r,steps},Pool=4);

KeyUpdatedFcn コールバックを設定します。ジョブの ValueStore オブジェクトを取得し、ジョブによって ValueStore オブジェクトにエントリが追加されたときに実行するコールバック関数を設定します。

各 parfor ループでジョブによって ValueStore オブジェクトにエントリが追加されると、コールバック関数 UpdatePlot が実行されます。この関数は、プロットを新しいデータで更新します。

ソフトウェアでの KeyUpdatedFcn コールバックの設定前に、ジョブによって ValueStore オブジェクトに情報が書き込まれる可能性があります。この動作を防ぐためにジョブの投入前に KeyUpdatedFcn コールバックを設定するには、関数createCommunicatingJobを使用します。

store = job.ValueStore;
store.KeyUpdatedFcn = @(store,key) updatePlot(ax1,ax2,store,key);

wait を使用してジョブへのアクティブな接続をライブ スクリプトで維持します。wait を使用すると、ジョブの実行中はコマンド ラインがブロックされます。あるいは、実行中もコマンド ラインを使用するには、この例のプレーン スクリプト バージョンを MATLAB コマンド ラインから呼び出します。プロットの更新に時間がかかる場合があります。

disp("Waiting for job to finish ...")

Waiting for job to finish ...

wait(job);
disp("Job completed")

Job completed

ジョブの終了後、ジョブの ValueStore オブジェクトに引き続きアクセスできます。ValueStore オブジェクトのデータにはキーを使用してアクセスできます。たとえば、ステップ 6 のデータを表示します。

disp("Fetching example result for step 6:")

Fetching example result for step 6:

resultFromStep6 = store("Step 6")

resultFromStep6 = struct with fields:
           step: 6
              x: 0.9460
              y: 0.4209
      in_circle: 0
    point_color: 'b'

ジョブの結果を取得し、ジョブを削除します。

pointsData = fetchOutputs(job);
delete(job)
clear job

サポート関数

モンテカルロ シミュレーション

関数 generatePoints は、正方形の中に点をランダムに配置します。この関数では、rand を使用して区間 (-r, r) の一様分布から 2 つの乱数 $\mathit{x}$ と $\mathit{y}$ を生成します。その後、関数は $\mathit{x}$ と $\mathit{y}$ の値で定義される点が円の内側にあるかどうかを判定し、$\mathit{x}$ と $\mathit{y}$ の値をジョブの ValueStore オブジェクトに一意のキーを付けて格納します。点が円の内側にある場合、関数はエントリに値 1 と赤色を割り当てます。点が円の外側にある場合、関数はエントリに値 0 と青色を割り当てます。ValueStore オブジェクトは、parfor ループの各反復で新しいエントリを取得します。ジョブのプロパティとしてアクセスできるスライス化された変数 points に結果を保存します。

function points = generatePoints(r,steps)
points = zeros(steps,4);
parfor idx = 1:steps
    x = (r+r)*rand - r;
    y = (r+r)*rand - r;
    pause(2) % Use pause to control the speed of the example.
    if sqrt(x^2 + y^2) < r
        points(idx,:,end) = [idx x y 1];
        point_color = 'r';
        in_circle = 1
    else
        points(idx,:,end) = [idx x y 0];
        point_color = 'b';
        in_circle = 0
    end

    % Get the ValueStore object of the current job.
    store = getCurrentValueStore;
    % Store the simulation results in the 
    % job ValueStore object with a unique key.
    key = "Step " + idx;
    store(key) = struct(step=idx,x=x,y=y, ...
        in_circle=in_circle,point_color=point_color);
end
end

結果のライブ更新

中間結果のプロットを使用して、モンテカルロによる π の推定の進行状況を監視します。関数 updatePlot は、ジョブで ValueStore オブジェクトが更新されるたびにプロットを更新します。

function updatePlot(ax1,ax2,store,key)
% Update results from the job ValueStore object.
result = store(key);

% Estimate pi with all the data stored in the ValueStore object.
keyset = keys(store); % Return all the keys of the ValueStore object. 
all_data = cell2mat(get(store,keyset)); % Convert to a structure array.
hits = [all_data.in_circle]; % Concatenate the result from each key.
pi_estimate = (sum(hits)*4)/(numel(hits)); 

% Update the plots with the new x and y values and the estimate of pi.
hold([ax1 ax2],'on');
plot(ax1,result.x,result.y,'.',Color=result.point_color);
plot(ax2,numel(hits),pi_estimate,".-k");
title(ax2,"Current Estimate of $\pi$",num2str(pi),Interpreter="latex");
hold([ax1 ax2],'off');
drawnow nocallbacks;
end

シンプルなモンテカルロ面積法

半径 "r" の円が各辺の長さ "2r" の正方形に内接している場合、円の面積と正方形の面積の関係が π で与えられます。次の図は、この問題を示したものです。

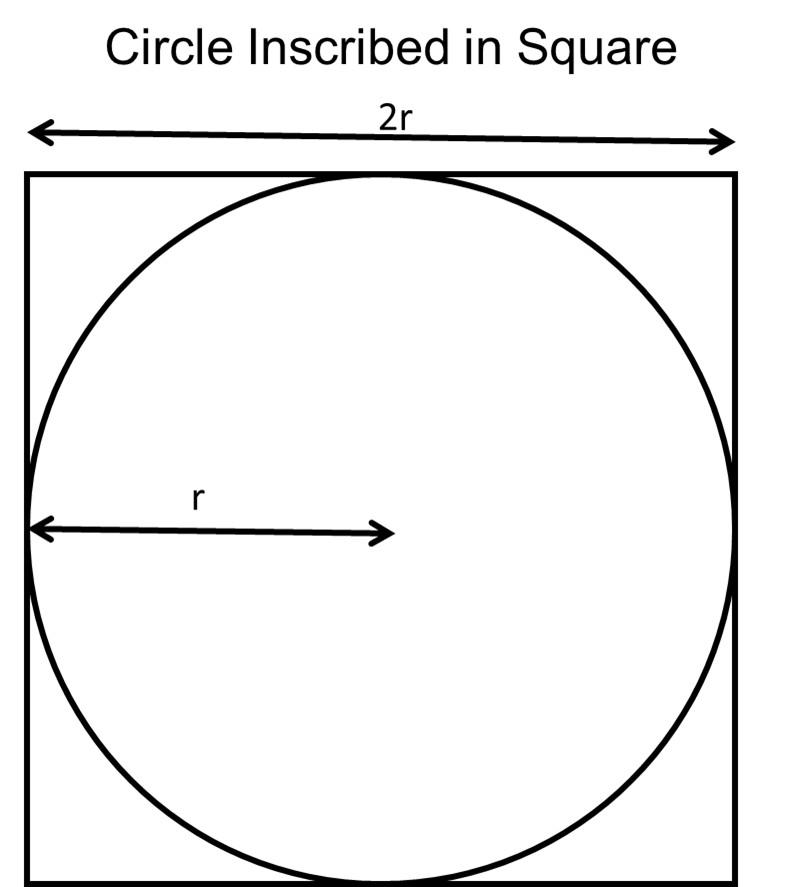
円の面積を正方形の面積で除算した比から π を導出できます。

$\frac{\mathrm{area}\mathrm{of}\mathrm{circle}}{\mathrm{area}\mathrm{of}\mathrm{square}}=$

$\frac{\pi {\mathit{r}}^2}{{\left(2\mathit{r}\right)}^2}=\frac{\pi }{4}$

π を直接使用せずに円の面積を推定するには、正方形の中に 2 次元の点の一様なサンプルをランダムに生成し、円の内側にある数をカウントします。点が円の内側にある確率は、円の面積を正方形の面積で除算した比になります。

点が円の内側にあるかどうかを判定するには、点の $\mathit{x}$ 座標と $\mathit{y}$ 座標の 2 つの値をランダムに生成し、点から円の原点までの距離を計算します。原点から生成された点までの距離 $\mathit{d}$ は、次の方程式で与えられます。

$$\mathit{d}=\sqrt{{\mathit{x}}^2+{\mathit{y}}^2}$$

$\mathit{d}$ が円の半径 $\mathit{r}$ よりも小さければ、点は円の内側にあります。大規模な点のサンプルを生成し、円の内側にある数をカウントします。このデータを使用して、円の内側にある点と生成された点の総数の比を取得します。この比は、円の面積と正方形の面積の比と等価です。これにより、以下を使用して π を推定できます。

$\frac{\mathrm{points}\mathrm{in}\mathrm{circle}}{\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{points}}\approx \frac{\pi }{4}$

$$\pi \approx 4\times \frac{\mathrm{points}\mathrm{in}\mathrm{circle}}{\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{points}}$$

参考

batch | ValueStore | createCommunicatingJob

関連するトピック

• ValueStore によるバッチ ジョブの監視
• バッチ ジョブの実行とワーカーからのファイルへのアクセス