Optimization Toolbox を使用したポートフォリオの分散化

この例では、ポートフォリオの資産分散化の 3 つの手法を示します。資産分散化の目的は、ある期間のボラティリティを低減するために、指定された任意の資産に対するポートフォリオのエクスポージャーのバランスを取ることです。実務者によっては、共分散行列の推定に対する最小分散ポートフォリオの感度を考慮して、出来高、最大ドローダウンなどの分散対策以外のリスク対策を最小限に抑える目的でポートフォリオ選択に分散化手法を加えている場合もあります。

この例では、以下の一般的な分散化手法を紹介します。

• 均等加重 (EW) ポートフォリオ

• 等リスク寄与度 (ERC)

• 最大分散ポートフォリオ (MDP)

さらに、この例では、さまざまな分散度を実現するために使用できるペナルティ法についても説明します。これらの方法では、目的関数にペナルティ項を追加して、分散低減の度合いとポートフォリオの分散化のバランスを取ります。

市場データの取得と平均分散ポートフォリオの定義

まず、期待される収益とその共分散行列を読み込み、計算を行います。

% Load data
load('port5.mat');
% Store returns and covariance
mu = mean_return;
Sigma = Correlation .* (stdDev_return * stdDev_return');

既定の制約をもつPortfolio (Financial Toolbox)オブジェクトを使用して平均分散ポートフォリオを定義し、完全投資の長期限定ポートフォリオを作成します。

% Create a mean-variance Portfolio object with default constraints
p = Portfolio('AssetMean',mu,'AssetCovar',Sigma);
p = setDefaultConstraints(p);

Portfolio (Financial Toolbox)オブジェクトの多くの機能の 1 つに、ポートフォリオ問題の効率的フロンティアを取得できる機能があります。効率的フロンティアを計算するには、ポートフォリオの収益レベル ${\mu }_0$ を変更し、効率的フロンティア上の異なる点を取得するようにして一連の最適化問題を解きます。このような問題は、次のように定義されます。

$$\begin{array}{l}\min {\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}\\ \mathrm{st}.\sum _{\mathit{i}=1}^{\mathit{n}}{\mathit{x}}_{\mathit{i}}=1\\ {\mathit{x}}^{\mathit{T}}\mu \ge {\mu }_0\\ \mathit{x}\ge 0\end{array}$$

Portfolio (Financial Toolbox)オブジェクトを使用して効率的フロンティアを計算すると、上記の複数の最適化問題を手作業で定式化して解かなくても、効率的フロンティアを求められるという利点があります。

plotFrontier(p);

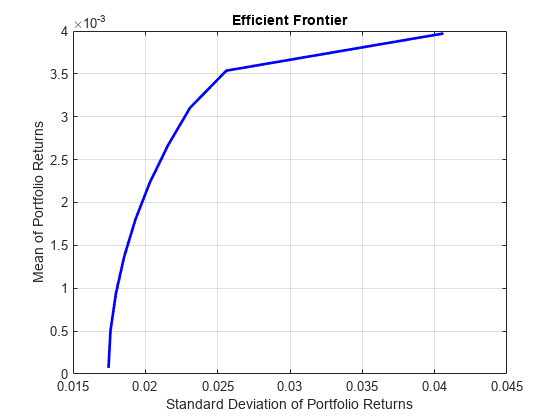
また、Portfolio (Financial Toolbox)オブジェクトは、次の問題によって定義される、最小分散ポートフォリオに関連付けられた重みを計算することもできます。

$$\begin{array}{l}\min {\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}\\ \mathrm{st}.\sum _{\mathit{i}=1}^{\mathit{n}}{\mathit{x}}_{\mathit{i}}=1\\ \mathit{x}\ge 0\end{array}$$

この最小分散の重みはベンチマークとみなされ、分散化手法の重みはすべて、この重みと比較されます。

wMinVar = estimateFrontierLimits(p,'min');

Portfolio (Financial Toolbox)オブジェクトは、最小分散ポートフォリオを計算できます。ただし、分散化手法により、ポートフォリオ問題の目的関数に修正が加えられますが、この修正は R2022b より前の MATLAB® バージョンのPortfolio (Financial Toolbox)オブジェクトではサポートされていません。以前のバージョンの場合は、Optimization Toolbox™ を使用して以下の問題を解く必要があります。Portfolio (Financial Toolbox)オブジェクトで解くことのできる問題の詳細については、When to Use Portfolio Objects Over Optimization Toolbox (Financial Toolbox)を参照してください。

分散化手法の指定

このセクションでは、3 つの分散化方法を紹介します。この 3 つの分散化方法のそれぞれを分散化指標と関連付け、その分散化指標を使用して、さまざまな分散度を実現するペナルティ項を定義します。目的関数にペナルティ項を追加して得られる分散化の範囲は、最小分散ポートフォリオによって実現される挙動から、それぞれ EW、ECR、および MDP の挙動までとなります。

最初にoptimproblemオブジェクトを初期化して、その制約を定義します。以下のポートフォリオ問題はすべて同じ制約をもち、目的関数のみが変化します。そのため、次のoptimproblemは再利用できますが、目的関数は適宜再定義されます。

% Define an optimization problem to adjust portfolio diversification
diverseProb = optimproblem('ObjectiveSense','minimize');

既定のポートフォリオは等式制約を 1 つだけもち、資産の重みに下限が設定されています。この重みは、非負かつそれらの和が 1 でなければなりません。実行可能なセットは $\mathit{X}$ として表現されます。

$$\mathit{X}=\left\{\mathit{x}|\mathit{x}\ge 0,\sum _{\mathit{i}=1}^{\mathit{n}}{\mathit{x}}_{\mathit{i}}=1\right\}$$

% Variables
nX = p.NumAssets;
% Porfolio weights [nX-by-1 vector]
x = optimvar('x',nX,1,'LowerBound',0); % x >= 0 (long-only portfolio)

% Equality constraint
% Sum of weights equal to one
diverseProb.Constraints.fullyInvested = sum(x) == 1;

例の最初の部分は、Portfolio (Financial Toolbox)オブジェクトを使用して最小分散ポートフォリオを計算する方法を示しています。ただし、最小分散の重みは、最小分散問題を表す次のコードで取得することもできます。

$$\underset{\mathit{x}\in \mathit{X}}{\min }{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}$$

% Minimize variance
diverseProb.Objective = x'*p.AssetCovar*x;
% Solution of minimum variance portfolio
opts = optimoptions('quadprog','Display','none'); % No output display
[wMinVar2,fMinVar,c,d,e] = solve(diverseProb,'options',opts);

上記の解とPortfolio (Financial Toolbox)オブジェクトで得られた解は、完全には一致しません。

norm(wMinVar-wMinVar2.x,inf)

ans = 0.0032

共分散行列の固有値の大きさを考慮すると最小分散問題が正しくスケーリングされないため、この結果が生じます。目的関数を大きな定数 (1e4 など) で再スケーリングすると、両方の解が数値の精度内で一致します。この機能は、Portfolio (Financial Toolbox)オブジェクトを使用するもう 1 つの利点となります。Portfolio (Financial Toolbox)オブジェクトは既定で問題を再スケーリングして数値問題を解決するため、問題をスケーリングしないで得られるポートフォリオより分散の小さいポートフォリオを取得します。

この例の目的はさまざまな分散化手法を示すことであるため、最適化問題を再スケーリングせずに進みます。ただし、分散項 (${\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}$) は、以下のいずれの問題においても再スケーリング可能であることに留意してください。

均等加重 (EW) ポートフォリオ

分散化指標の 1 つに、次のように定義されるハーフィンダール・ハーシュマン (HH) 指数があります。

$$\mathrm{HH}\left(\mathit{x}\right)=\sum _{\mathit{i}=1}^{\mathit{n}}{\mathit{x}}_{\mathit{i}}^2$$

この指数は、ポートフォリオが均等加重の場合に最小となります。この指数をペナルティとして使用して得られたポートフォリオは、ポートフォリオの制約を満たし、より均等に重み付けされた重みをもちます。

HH 指数を最小化するポートフォリオは $\underset{\mathit{x}\in \mathit{X}}{\min }{\mathit{x}}^{\mathit{T}}\mathit{x}$ で表されます。$\mathit{X}$ の制約は既定の制約であるため、この問題の解は EW ポートフォリオです。$\mathit{X}$ に追加制約がある場合は、すべての制約を満たすと同時に、重みを可能な限り均等に保つポートフォリオが解となります。

% Maximize the HH diversification (by minimizing the HH index)
diverseProb.Objective = x'*x;
% Solution that minimizes the HH index
[wHH,fHH] = solve(diverseProb,'options',opts);

HH ペナルティを含む、分散を最小化するポートフォリオは $\underset{\mathit{x}\in \mathit{X}}{\min }{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}+{\lambda }_{\mathrm{HH}}{\mathit{x}}^{\mathit{T}}\mathit{x}$ で表されます。

% HH penalty parameter
lambdaHH = 1e-2;
% Variance + Herfindahl-Hirschman (HH) index
diverseProb.Objective = x'*p.AssetCovar*x + lambdaHH*(x'*x);
% Solution that accounts for risk and HH diversification
[wHHMix,fHHMix] = solve(diverseProb,'options',opts);

最小分散ポートフォリオ、均等加重ポートフォリオ、およびペナルティを含む手法の重み分布をプロットします。

% Plot different strategies
plotAssetAllocationChanges(wMinVar,wHHMix.x,wHH.x)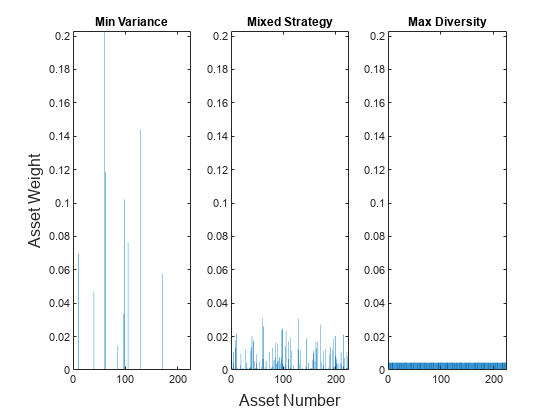

このプロットは、最小分散ポートフォリオと EW ポートフォリオの中間となる重みが、ペナルティを含む手法によりどのように返されるかを示しています。実際、${\lambda }_{\mathrm{HH}}=0$ を選択すると最小分散解が返され、${\lambda }_{\mathrm{HH}}\to \infty ,$ とすると解が EW ポートフォリオに近づきます。

最大分散ポートフォリオ (MDP)

最大分散ポートフォリオ (MDP) に関連付けられた分散化指数は、次のように定義されます。

$$\mathrm{MDP}\left(\mathit{x}\right)=-\sum _{\mathit{i}=1}^{\mathit{n}}{\sigma }_{\mathit{i}}{\mathit{x}}_{\mathit{i}}$$

ここで、${\sigma }_{\mathit{i}}$ は資産 $\mathit{i}$ の標準偏差を表します。

MDP は、次の分散度を最大化するポートフォリオです。

$$\phi \left(\mathit{x}\right)=\frac{{\mathit{x}}^{\mathit{T}}\sigma }{\sqrt{{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}}}$$

ポートフォリオが 1 つの資産に完全投資されている場合、またはすべての資産が完全相関にある場合、分散度 $\phi \left(\mathit{x}\right)$ は 1 に等しくなります。それ以外の場合は、$\phi \left(\mathit{x}\right)>1$ です。$\phi \left(\mathit{x}\right)\approx 1$ の場合は分散化されていないため、$\phi \left(\mathit{x}\right)$ を最大化するポートフォリオを見つけることが目標となります。

$$\underset{\mathit{x}\in \mathit{X}}{\max }\frac{{\sigma }^{\mathit{T}}\mathit{x}}{\sqrt{{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}}}$$

上記の非線形、非凸の最適化問題を解く代わりに、問題は等価な二次凸問題として書き換えられます。この再定式化は、シャープ レシオを最大化するときに使用されるものと同じ考え方に則っています (Cornuejols および Tütüncü [3])。等価な二次問題により、以下が得られます。

$$\begin{array}{l}\underset{\mathit{y}\ge 0,\tau \ge 0}{\min }{\mathit{y}}^{\mathit{T}}\Sigma \mathit{y}\\ \mathit{s}.\mathit{t}{\sigma }^{\mathit{T}}\mathit{y}=1\\ \sum _{\mathit{i}=1}^{\mathit{n}}{\mathit{y}}_{\mathit{i}}=\tau \end{array}$$

ここで、MDP 指数の負の値が、問題に対する制約として表示されます。ここで、MDP の重みは $\frac{\mathit{y}}{\tau }$ で与えられます。

HH 指数とは異なり、MDP の目標は、すべての資産で重みが均等に分散されたポートフォリオを取得することではなく、選択された (非ゼロの) 資産が全体としてポートフォリオに同じ相関をもつポートフォリオを取得することです。

% MDP problem
MDPprob = optimproblem('ObjectiveSense','minimize');

% Variables
% Surrogate portfolio weights
y = optimvar('y',nX,1,'LowerBound',0); % y >= 0 (long-only portfolio)
% Auxiliary variable
tau = optimvar('tau',1,1,'LowerBound',0); % tau >= 0

% Constraints
% Sum of stds equal to one
sigma = sqrt(diag(p.AssetCovar));
MDPprob.Constraints.sigmaSumToOne = sigma'*y == 1;
% Sum of weights equal to tau
MDPprob.Constraints.sumToTau = sum(y) == tau;

% Objective
%   min y'*Sigma*y
MDPprob.Objective = y'*p.AssetCovar*y;

% Solve for the MDP
[wMDP,fMDP] = solve(MDPprob,'options',opts);
xMDP = wMDP.y/wMDP.tau;

次のコードは、MDP 問題とそのペナルティを含むバージョンの問題が等価になるような値 ${\hat{\lambda }}_{\mathrm{MDP}}>0$ が存在することを示しています。MDP ペナルティを含む、分散を最小化するポートフォリオは $\underset{\mathit{x}\in \mathit{X}}{\min }{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}-{\lambda }_{\mathrm{MDP}}{\sigma }^{\mathit{T}}\mathit{x}$ で表されます。

MDP ペナルティ パラメーターを定義し、MDP を求めます。

% MDP penalty parameter
lambdaMDP = 1e-2;
% Variance + Most Diversified Portfolio (MDP)
diverseProb.Objective = x'*p.AssetCovar*x - lambdaMDP*(sigma'*x);
% Solution that accounts for risk and MDP diversification
[wMDPMix,fMDPMix] = solve(diverseProb,'options',opts);

最小分散ポートフォリオ、MDP、およびペナルティを含む手法の重み分布をプロットします。

% Plot different strategies
plotAssetAllocationChanges(wMinVar,wMDPMix.x,xMDP)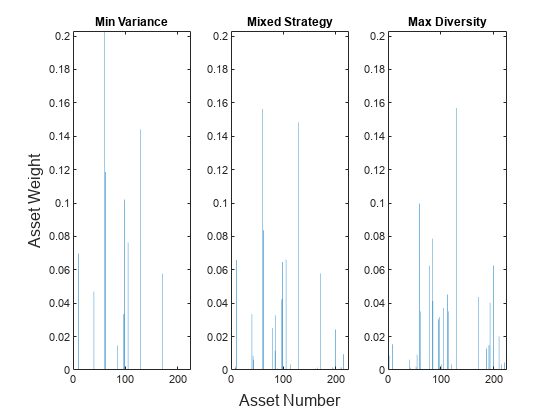

このプロットで、ペナルティを含む手法の重みは、最小分散ポートフォリオと MDP の中間にあります。この結果は HH ペナルティを含む場合と同じであり、${\lambda }_{\mathrm{MDP}}=0$ を選択すると最小分散解が返され、${\lambda }_{\mathrm{MDP}}\in \left[0,{\hat{\lambda }}_{\mathrm{MDP}}\right]$ の値は最小分散挙動から MDP 挙動までの範囲の資産の重みを返します。

等リスク寄与度 (ERC) ポートフォリオ

等リスク寄与度 (ERC) ポートフォリオに関連付けられた分散化指数は、次のように定義されます。

$$\mathrm{ERC}\left(\mathit{x}\right)=-\sum _{\mathit{i}=1}^{\mathit{n}}\ln \left({\mathit{x}}_{\mathit{i}}\right)$$

この指数は、Maillard [1] が示した、ERC ポートフォリオの計算に使用される凸再定式化に関連します。この著者らは、次の最適化問題を解き、

$$\begin{array}{l}\underset{\mathit{y}\ge 0}{\min }{\mathit{y}}^{\mathit{T}}\Sigma \mathit{y}\\ \mathrm{st}.\sum _{\mathit{i}=1}^{\mathit{n}}\ln \left({\mathit{x}}_{\mathit{i}}\right)\ge \mathit{c}\end{array}$$

既定の制約をもつ ERC ポートフォリオである $\mathit{x}$ を $\mathit{x}=\frac{\mathit{y}}{{\sum }_{\mathit{i}}{\mathit{y}}_{\mathit{i}}}$ として定義することで、ERC ポートフォリオを取得できることを示しています。ここで、$\mathit{c}>0$ は任意の定数です。

ERC ポートフォリオの目的は、ポートフォリオのボラティリティに対する各資産のリスク寄与が、すべての資産について同じとなるように資産の重みを選択することです。

% ERC portfolio
ERCprob = optimproblem('ObjectiveSense','minimize');

% Variables
% Surrogate portfolio weights
y = optimvar('y',nX,1,'LowerBound',0); % y >= 0 (long-only portfolio)

% Constraints
% Log constraint
ERCprob.Constraints.logSumIneq = sum(log(y)) >= 1;

% Objective
%   min y'*Sigma*y
ERCprob.Objective = y'*p.AssetCovar*y;

% Solve a nonlinear problem for the ERC portfolio
opts = optimoptions('fmincon','Display','none'); % No output display
w0.y = wMinVar; % Define starting point for fmincon
[wERC,fERC] = solve(ERCprob,w0,'options',opts);
xERC = wERC.y/sum(wERC.y);

ERC ペナルティを含む、分散を最小化するポートフォリオは $$\underset{\mathit{x}\in \mathit{X}}{\min }{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}-{\lambda }_{\mathrm{ERC}}\sum _{\mathit{i}=1}^{\mathit{n}}\ln \left({\mathit{x}}_{\mathit{i}}\right)$$ で表されます。

ペナルティを含む MDP の定式化の場合と同様、ERC 問題とそのペナルティを含むバージョンが等価になるような ${\hat{\lambda }}_{\mathrm{ERC}}$ が存在します。

% ERC penalty parameter
lambdaERC = 3e-6; % lambdaERC is so small because the log of a number
                  % close to zero (the portfolio weights) is large.
% Variance + Equal Risk Contribution (ERC)
diverseProb.Objective = x'*p.AssetCovar*x - lambdaERC*sum(log(x));
% Solution that accounts for risk and ERC diversification
[wERCMix,fERCMix] = solve(diverseProb,wHH,'options',opts);

最小分散ポートフォリオ、ERC、およびペナルティを含む手法の重み分布をプロットします。

% Plot different strategies
plotAssetAllocationChanges(wMinVar,wERCMix.x,xERC)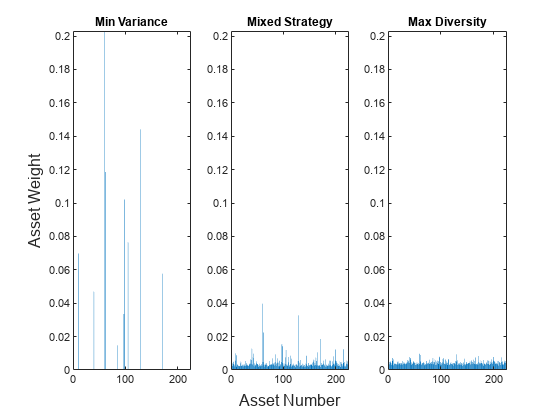

上記 2 つの分散化指標と同様、ここでもペナルティを含む手法の重みは最小分散ポートフォリオと ERC ポートフォリオの中間にあります。${\lambda }_{\mathrm{ERC}}=0$ を選択すると最小分散解が返され、${\lambda }_{\mathrm{ERC}}\in \left[0,{\hat{\lambda }}_{\mathrm{ERC}}\right]$ の値は最小分散挙動から ERC ポートフォリオ挙動までの範囲の資産の重みを返します。

分散化手法の比較

各ポートフォリオで選択されている資産の数を計算します。資産に関連付けられている重みが、あるしきい値を超えている場合にその資産が選択されているとみなします。

% Build a weights table
varNames = {'MinVariance','MixedHH','HH','MixedMDP','MDP', ...
    'MixedERC','ERC'};
weightsTable = table(wMinVar,wHHMix.x,wHH.x,wMDPMix.x,xMDP, ...
    wERCMix.x,xERC,'VariableNames',varNames);
% Number of assets with nonzero weights
cutOff = 1e-3; % Weights below cut-off point are considered zero.
[reweightedTable,TnonZero] = tableWithNonZeroWeights(weightsTable, ...
    cutOff,varNames);
display(TnonZero)

TnonZero=1×7 table
                       MinVariance    MixedHH    HH     MixedMDP    MDP    MixedERC    ERC
                       ___________    _______    ___    ________    ___    ________    ___

    Nonzero weights        11           104      225       23       28       225       225

上記で説明したとおり、より均等に重み付けされたポートフォリオを取得することが HH ペナルティの目標です。HH の分散性を最大化する (既定の制約が選択された場合にのみ EW ポートフォリオに対応する) ポートフォリオでは最大数の資産が選択されており、これらの資産の重みはより近いものとなります。この後半部分の品質については、次のboxchartで確認されます。また、HH 指数をペナルティ関数として目的関数に追加する手法の資産の数は、最小分散ポートフォリオよりも多く、HH の分散性を最大化するポートフォリオよりも少なくなります。ERC ポートフォリオでも、ある程度のリスク寄与を設定するためにすべての重みを非ゼロとする必要があるため、すべての資産が選択されます。

% Boxchart of portfolio's weights
figure;
matBoxPlot = reweightedTable.Variables;
matBoxPlot(matBoxPlot == 0) = NaN;
boxchart(matBoxPlot)
xticklabels(varNames)
title('Weights Distribution')
xlabel('Strategies')
ylabel('Weight')

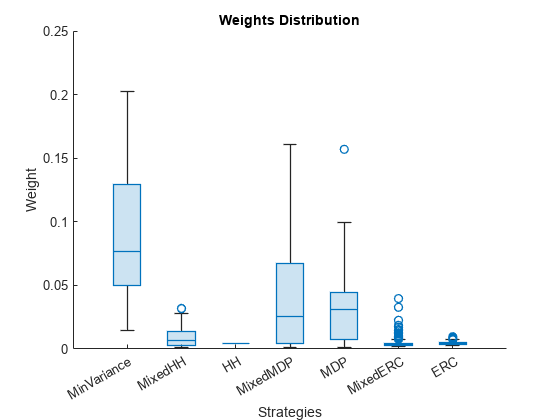
このboxchartは、さまざまなポートフォリオに対する資産の正の重みの広がりを示します。前述したとおり、HH の分散性を最大化するポートフォリオの重みは、すべて同じです。ポートフォリオに他のタイプの制約がある場合、重みはすべて同じにはなりませんが、その分散は最も小さくなります。また、ERC ポートフォリオの重みの分散も小さくなります。実際、資産の数が増えるに従い、ERC ポートフォリオの重みの分散は小さくなることが分かります。

MDP の重みの変動性は、最小分散の重みの変動性より小さくなります。ただし、MDP の目標は、均等に重み付けされた資産を取得することではなく、各資産のそのポートフォリオとの相関を均等に分散させることであるため、必ずしも MDP の重みの変動性が最小分散の重みより小さくなるとは限りません。

% Compute and plot the risk contribution of each individual
% asset to the portfolio
riskContribution = portfolioRiskContribution(p.AssetCovar,...
    weightsTable.Variables);
% Remove small contributions
riskContribution(riskContribution < 1e-3) = NaN;

% Compare percent contribution to portofolio risk
boxchart(riskContribution)
xticklabels(varNames)
title('Percent Contributions to Portfolio Risk')
xlabel('Strategies')
ylabel('PCRs')

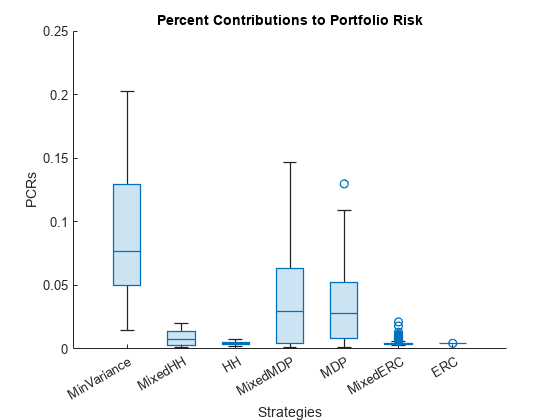
このboxchartは、ポートフォリオ全体のリスクに対する各資産のリスク寄与度を示します。リスク寄与度は、次のように計算されます。

$${\left(\mathrm{PRC}\right)}_{\mathit{i}}=\frac{{\mathit{x}}_{\mathit{i}}{\left(\Sigma \mathit{x}\right)}_{\mathit{i}}}{{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}}$$

想定したとおり、すべての ERC ポートフォリオの資産で、ポートフォリオに対するリスク寄与は同じです。重み分布のプロットの後で説明したとおり、ポートフォリオに他のタイプの制約がある場合、ERC ポートフォリオのリスク寄与は、すべての資産について同じにはなりませんが、その分散は最も小さくなります。また、この図に示された挙動は、重みの分布により示された挙動と類似しています。

% Compute and plot the correlation of each individual asset to its
% portfolio
corrAsset2Port = correlationInfo(p.AssetCovar,...
    weightsTable.Variables);
% Boxplot of assets to portfolio correlations
figure
boxchart(corrAsset2Port)
xticklabels(varNames)
title('Correlation of Individual Assets to Their Portfolio')
xlabel('Strategies')
ylabel('Correlation')

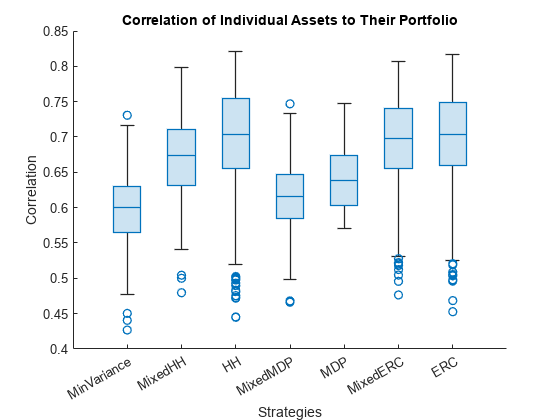
このboxchartは、各資産の、それぞれのポートフォリオとの相関の分布を示します。ポートフォリオに対する資産 $\mathit{i}$ の相関は、次の式で計算されます。

$${\rho }_{\mathrm{iP}}=\frac{{\left(\Sigma \mathit{x}\right)}_{\mathit{i}}}{{\sigma }_{\mathit{i}}\sqrt{{\mathit{x}}^{\mathit{T}}\Sigma \mathit{x}}}$$

MDP は相関がより近接したポートフォリオであり、MDP ペナルティ項を使用する手法に従います。実際、ポートフォリオ問題で負の重みが許される場合、MDP のすべての資産はそのポートフォリオに対して同じ相関をもちます。また、HH (EW) と ERC ポートフォリオの相関変動性はどちらもほぼ同じになります。

参考文献

1. Maillard, S., Roncalli, T., & Teïletche, J. "The Properties of Equally Weighted Risk Contribution Portfolios." The Journal of Portfolio Management, 36(4), 2010, pp. 60-70.

2. Richard, J. C., & Roncalli, T. "Smart Beta: Managing Diversification of Minimum Variance Portfolios." Risk-Based and Factor Investing. Elsevier, 2015, pp. 31-63.

3. Tütüncü, R., Peña, J., Cornuéjols, G. Optimization Methods in Finance. United Kingdom: Cambridge University Press, 2018.

ローカル関数

function [] = plotAssetAllocationChanges(wMinVar,wMix,wMaxDiv)
% Plots the weights' allocation from the strategies shown before 

figure
t = tiledlayout(1,3);
nexttile
bar(wMinVar')
axis([0 225 0 0.203])
title('Min Variance')
nexttile
bar(wMix')
axis([0 225 0 0.203])
title('Mixed Strategy')
nexttile
bar(wMaxDiv')
axis([0 225 0 0.203])
title('Max Diversity')
ylabel(t,'Asset Weight')
xlabel(t,'Asset Number')

end

function [weightsTable,TnonZero] = ...
    tableWithNonZeroWeights(weightsTable,cutOff,varNames)
% Creates a table with the number of nonzero weights for each strategy

% Select only meaningful weights
funSelect = @(x) (x >= cutOff).*x./sum(x(x >= cutOff));
weightsTable = varfun(funSelect,weightsTable);

% Number of assets with positive weights
funSum = @(x) sum(x > 0);
TnonZero = varfun(funSum,weightsTable);
TnonZero.Properties.VariableNames = varNames;
TnonZero.Properties.RowNames = {'Nonzero weights'};

end

function [corrAsset2Port] = correlationInfo(Sigma,portWeights)
% Returns a matrix with the correlation of each individual asset to its
% portfolio

nX = size(portWeights,1); % Number of assets
nP = size(portWeights,2); % Number of portfolios

auxM = eye(nX);
corrAsset2Port = zeros(nX,nP);
for j = 1:nP
    % Portfolio's standard deviation
    sigmaPortfolio = sqrt(portWeights(:,j)'*Sigma*portWeights(:,j));
    for i = 1:nX
        % Assets's standard deviation
        sigmaAsset = sqrt(Sigma(i,i));
        % Asset to portfolio correlation
        corrAsset2Port(i,j) = (auxM(:,i)'*Sigma*portWeights(:,j))/...
            (sigmaAsset*sigmaPortfolio);
    end
end

end

function [riskContribution] = portfolioRiskContribution(Sigma,...
    portWeights)
% Returns a matrix with the risk contribution of each asset to
% the underlying portfolio.

nX = size(portWeights,1); % Number of assets
nP = size(portWeights,2); % Number of portfolios

riskContribution = zeros(nX,nP);
for i = 1:nP
    weights = portWeights(:,i);
    % Portfolio variance
    portVar = weights'*Sigma*weights;
    % Marginal constribution to portfoli risk (MCR)
    margRiskCont = weights.*(Sigma*weights)/sqrt(portVar);
    % Percent contribution to portfolio risk
    riskContribution(:,i) = margRiskCont/sqrt(portVar);
end

end

参考

Portfolio (Financial Toolbox)

関連するトピック

• 問題ベースの最適化ワークフロー
• Diversify Portfolios Using Custom Objective (Financial Toolbox)