さまざまな問題ベースのアプローチを使用した非線形データ適合

最小二乗問題の設定に関する一般的なアドバイスは、最小二乗形式の問題であることを solve が認識できるよう、問題を定式化することです。そうすると、solve は内部的に lsqnonlin を呼び出すため、最小二乗問題を効率的に解くことができます。詳細については、問題ベースの最小二乗法の目的関数の記述を参照してください。

この例では、同じ問題に対する lsqnonlin と fminunc のパフォーマンスを比較することで、最小二乗法ソルバーの効率を示します。また、問題の線形部分を明示的に認識して個別に処理することで得られる付加的な利点についても説明します。

問題の設定

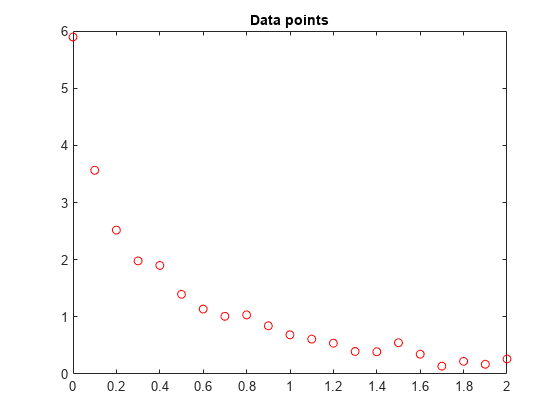
以下のデータを考えます。

Data = ...
  [0.0000    5.8955
   0.1000    3.5639
   0.2000    2.5173
   0.3000    1.9790
   0.4000    1.8990
   0.5000    1.3938
   0.6000    1.1359
   0.7000    1.0096
   0.8000    1.0343
   0.9000    0.8435
   1.0000    0.6856
   1.1000    0.6100
   1.2000    0.5392
   1.3000    0.3946
   1.4000    0.3903
   1.5000    0.5474
   1.6000    0.3459
   1.7000    0.1370
   1.8000    0.2211
   1.9000    0.1704
   2.0000    0.2636];

データ点をプロットします。

t = Data(:,1);
y = Data(:,2);
plot(t,y,'ro')
title('Data points')

この問題では、関数

y = c(1)*exp(-lam(1)*t) + c(2)*exp(-lam(2)*t)

をデータに近似したいと思います。

既定のソルバーを使用した解法

まず、方程式に対応する最適化変数を定義します。

c = optimvar('c',2);
lam = optimvar('lam',2);

次のように、初期点 x0 を任意に設定します。c(1) = 1、c(2) = 1、lam(1) = 1、lam(2) = 0。

x0.c = [1,1];
x0.lam = [1,0];

パラメーターが c および lam である場合に、時間 t での応答の値を計算する関数を作成します。

diffun = c(1)*exp(-lam(1)*t) + c(2)*exp(-lam(2)*t);

diffun を、この関数とデータ y の差の二乗和を求める最適化式に変換します。

diffexpr = sum((diffun - y).^2);

diffexpr を目的関数とする最適化問題を作成します。

ssqprob = optimproblem('Objective',diffexpr);

既定のソルバーを使用して、問題を解きます。

[sol,fval,exitflag,output] = solve(ssqprob,x0)

Solving problem using lsqnonlin.

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

sol = struct with fields:
      c: [2x1 double]
    lam: [2x1 double]

fval = 0.1477

exitflag = 
    FunctionChangeBelowTolerance

output = struct with fields:
           firstorderopt: 7.8870e-06
              iterations: 6
               funcCount: 7
            cgiterations: 0
               algorithm: 'trust-region-reflective'
                stepsize: 0.0096
                 message: 'Local minimum possible....'
            bestfeasible: []
         constrviolation: []
     objectivederivative: "forward-AD"
    constraintderivative: "closed-form"
                  solver: 'lsqnonlin'

返された解の値 sol.c および sol.lam に基づいて、得られた曲線をプロットします。

resp = evaluate(diffun,sol);
hold on
plot(t,resp)
hold off

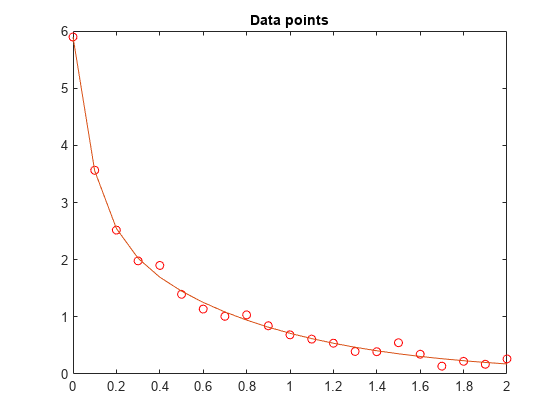
可能な限り適切に近似されているように見えます。

fminunc を使用した解法

fminunc ソルバーを使用して問題を解くには、solve を呼び出す際に 'Solver' オプションを 'fminunc' に設定します。

[xunc,fvalunc,exitflagunc,outputunc] = solve(ssqprob,x0,'Solver',"fminunc")

Solving problem using fminunc.

Local minimum found.

Optimization completed because the size of the gradient is less than
the value of the optimality tolerance.

xunc = struct with fields:
      c: [2x1 double]
    lam: [2x1 double]

fvalunc = 0.1477

exitflagunc = 
    OptimalSolution

outputunc = struct with fields:
             iterations: 30
              funcCount: 37
               stepsize: 0.0017
           lssteplength: 1
          firstorderopt: 2.9454e-05
              algorithm: 'quasi-newton'
                message: 'Local minimum found....'
    objectivederivative: "forward-AD"
                 solver: 'fminunc'

fminunc を使用して lsqcurvefit と同じ解が得られましたが、より多くの関数評価を行ったことに注意してください。fminunc のパラメーターは、lsqcurvefit のパラメーターとは逆の順序になります。より大きな lam は lam(1) ではなく lam(2) です。変数の順序は任意なので、これは当然です。

fprintf(['There were %d iterations using fminunc,' ...
    ' and %d using lsqcurvefit.\n'], ...
    outputunc.iterations,output.iterations)

There were 30 iterations using fminunc, and 6 using lsqcurvefit.

fprintf(['There were %d function evaluations using fminunc,' ...
    ' and %d using lsqcurvefit.'], ...
    outputunc.funcCount,output.funcCount)

There were 37 function evaluations using fminunc, and 7 using lsqcurvefit.

線形問題と非線形問題の分割

近似問題は、パラメーター c(1) および c(2) について線形であることに注意してください。これは、lam(1) と lam(2) の任意の値に対して、バックスラッシュ演算子を使用して、最小二乗問題を解く c(1) と c(2) の値を見つけることができるということを意味します。

2 次元問題として問題を解き直し、lam(1) および lam(2) の最適な値を探します。c(1) および c(2) の値は、上記で説明したように、バックラッシュ演算子を使用して各ステップで計算されます。これを行うには、関数 fitvector を使用します。この関数では、バックスラッシュ演算を行い、ソルバーの反復ごとに c(1) および c(2) を取得します。

type fitvector

function yEst = fitvector(lam,xdata,ydata)
%FITVECTOR  Used by DATDEMO to return value of fitting function.
%   yEst = FITVECTOR(lam,xdata) returns the value of the fitting function, y
%   (defined below), at the data points xdata with parameters set to lam.
%   yEst is returned as a N-by-1 column vector, where N is the number of
%   data points.
%
%   FITVECTOR assumes the fitting function, y, takes the form
%
%     y =  c(1)*exp(-lam(1)*t) + ... + c(n)*exp(-lam(n)*t)
%
%   with n linear parameters c, and n nonlinear parameters lam.
%
%   To solve for the linear parameters c, we build a matrix A
%   where the j-th column of A is exp(-lam(j)*xdata) (xdata is a vector).
%   Then we solve A*c = ydata for the linear least-squares solution c,
%   where ydata is the observed values of y.

A = zeros(length(xdata),length(lam));  % build A matrix
for j = 1:length(lam)
   A(:,j) = exp(-lam(j)*xdata);
end
c = A\ydata; % solve A*c = y for linear parameters c
yEst = A*c; % return the estimated response based on c

solve を使用して問題を解きます。2 次元の初期点 x02.lam = [1,0] から始めます。これを行うには、まず、fcn2optimexpr を使用して、関数 fitvector を最適化式に変換します。詳細については、非線形関数から最適化式への変換を参照してください。警告を回避するために、結果の式の出力サイズを指定します。変換後の関数 fitvector とデータ y の差の二乗和を目的として、新しい最適化問題を作成します。

x02.lam = x0.lam;
F2 = fcn2optimexpr(@(x) fitvector(x,t,y),lam,'OutputSize',[length(t),1]);
ssqprob2 = optimproblem('Objective',sum((F2 - y).^2));
[sol2,fval2,exitflag2,output2] = solve(ssqprob2,x02)

Solving problem using lsqnonlin.

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

sol2 = struct with fields:
    lam: [2x1 double]

fval2 = 0.1477

exitflag2 = 
    FunctionChangeBelowTolerance

output2 = struct with fields:
           firstorderopt: 4.4087e-06
              iterations: 10
               funcCount: 33
            cgiterations: 0
               algorithm: 'trust-region-reflective'
                stepsize: 0.0080
                 message: 'Local minimum possible....'
            bestfeasible: []
         constrviolation: []
     objectivederivative: "finite-differences"
    constraintderivative: "closed-form"
                  solver: 'lsqnonlin'

2 次元解法の効率は、4 次元解法の効率と同等です。

fprintf(['There were %d function evaluations using the 2-d ' ...
    'formulation, and %d using the 4-d formulation.'], ...
    output2.funcCount,output.funcCount)

There were 33 function evaluations using the 2-d formulation, and 7 using the 4-d formulation.

初期推定に対してよりロバストな分割問題

元の 4 パラメーター問題に対して不適切な始点を選択すると、大域的でない局所的な解がもたらされます。分割 2 パラメーター問題に対して、同じ不適切な lam(1) および lam(2) の値をもつ始点を選択すると、大域的な解がもたらされます。これを示すために、相対的に不適切である局所的な解をもたらす始点をもつ元の問題を再実行し、大域的な解によって得られた近似と比較します。

x0bad.c = [5 1];
x0bad.lam = [1 0];
[solbad,fvalbad,exitflagbad,outputbad] = solve(ssqprob,x0bad)

Solving problem using lsqnonlin.

Local minimum possible.

lsqnonlin stopped because the final change in the sum of squares relative to 
its initial value is less than the value of the function tolerance.

solbad = struct with fields:
      c: [2x1 double]
    lam: [2x1 double]

fvalbad = 2.2173

exitflagbad = 
    FunctionChangeBelowTolerance

outputbad = struct with fields:
           firstorderopt: 0.0036
              iterations: 31
               funcCount: 32
            cgiterations: 0
               algorithm: 'trust-region-reflective'
                stepsize: 0.0012
                 message: 'Local minimum possible....'
            bestfeasible: []
         constrviolation: []
     objectivederivative: "forward-AD"
    constraintderivative: "closed-form"
                  solver: 'lsqnonlin'

respbad = evaluate(diffun,solbad);
hold on
plot(t,respbad,'g')
legend('Data','Global fit','Bad local fit','Location','NE')
hold off

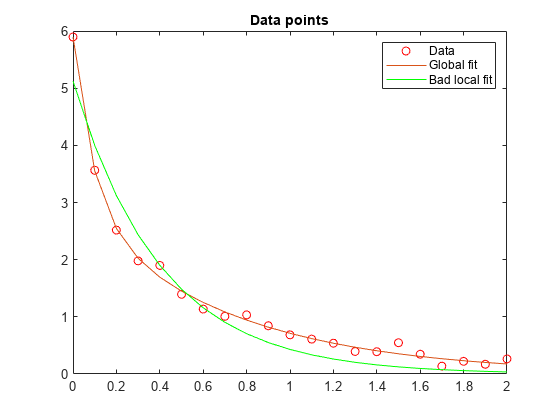
fprintf(['The residual norm at the good ending point is %f,' ...
   ' and the residual norm at the bad ending point is %f.'], ...
   fval,fvalbad)

The residual norm at the good ending point is 0.147723, and the residual norm at the bad ending point is 2.217300.

参考

solve | fcn2optimexpr

関連するトピック

• 非線形データ適合
• 問題ベースの最適化ワークフロー