Simulink モデルでの `lsqnonlin`

この例では次を使用します。

この例では、Simulink® モデルのパラメーターを調整する方法を示します。この例を実行すると、モデル optsim が含まれます。このモデルは Simulink ブロック線図としてモデル化された非線形プロセスプラントを含みます。

飽和要素を含むアクチュエータをもつプラント

このプラントは、アクチュエータに制限をもつ低減衰の 3 次のモデルです。アクチュエータは、飽和制限とスルーレート制限をもちます。アクチュエータの飽和制限により、入力値が最大 2 単位、最小 -2 単位の範囲に制限されます。そしてその変化率も 0.8 単位 / 秒以内としています。ステップ入力のシステムの閉ループ応答を閉ループ応答に示します。(コマンドラインで optsim と入力するか、モデル名をクリックして) モデルを開き、[シミュレーション] メニューから [実行] を選択すると、この応答を確認できます。応答は Scope ブロックにプロット表示されます。

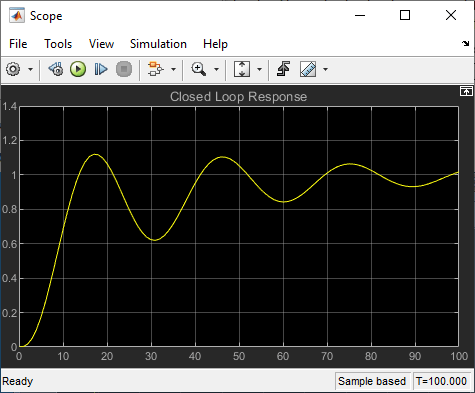
閉ループ応答

問題は、システムへの単位ステップ入力をトラックするフィードバック制御ループの設計です。閉ループプラントは、プラントとアクチュエータをまとめて 1 つの階層構造の Subsystem ブロックとして表します。Scope ブロックは、設計プロセスの間、出力軌跡を表示します。

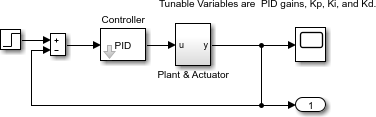
閉ループモデル

この問題を解くには、出力と入力信号の間の誤差を最小化します。(対照的に、Simulink モデルでの fminimax の使用の例では、解には出力の最大値を最小化することが含まれます。) 変数は比例積分係数 (PID) コントローラーのパラメーターです。誤差の最小化をある時間単位で行う場合、スカラー目的関数を使用できます。しかし、0 から 100 までの全タイムステップでの誤差の最小化をゴールとする場合、多目的関数 (各タイムステップに対して 1 つの目的関数) を作成します。

lsqnonlin を使用して、出力のトラッキングに対して最小二乗適合を実行します。トラッキングは関数 tracklsq より実行されます。この関数は、この例の終わりにある runtracklsq の中で入れ子になっています。tracklsq は、sim を呼び出すことにより計算された出力から入力信号 1 を差し引いた誤差信号 yout を返します。

関数 runtracklsq は必要な値すべてを設定し、目的関数 tracklsq を使用して lsqnonlin を呼び出します。lsqnonlin に渡す変数 options は、種々の変数やシミュレーションパラメーターの規範を設定したり、表示特性を定義します。出力を非表示とすること、そして 'levenberg-marquardt' アルゴリズムを使用することが各オプションにより指定されています。また、これらのオプションは 0.001 のオーダーでステップや目的関数に対する終了許容誤差を設定します。

モデル optsim でシミュレーションを実行するには、変数 Kp、Ki、Kd、a1、a2 (a1 と a2 は Plant ブロックの中の変数) を定義しなければなりません。Kp、Ki、Kd が最適化される変数です。関数 tracklsq は変数 a1 と a2 が 2 つの関数間で共有されるように runtracklsq の中で入れ子になっています。変数 a1 と a2 は runtracklsq 内で初期化されます。

目的関数 tracklsq はシミュレーションを実行します。シミュレーションはベースワークスペースまたは現在のワークスペース、すなわち sim を呼び出している関数のワークスペース (この場合では tracklsq のワークスペース) のいずれかで実行することができます。この例では SrcWorkspace オプションを 'Current' に設定して、sim に現在のワークスペースでシミュレーションを実行するように命令しています。runtracklsq はこのシミュレーションを 100 秒まで実行します。

シミュレーションが完了すると、runtracklsq は、現在のワークスペース (つまり、tracklsq のワークスペース) に myobj オブジェクトを作成します。ブロック線図モデルの Outport ブロックによって、シミュレーションの終わりにオブジェクトの yout フィールドが現在のワークスペースに出力されます。

runtracklsq を実行すると、最適化によって、コントローラーの比例、積分、微分 (Kp、Ki、Kd) ゲインの解が求められます。

[Kp, Ki, Kd] = runtracklsq

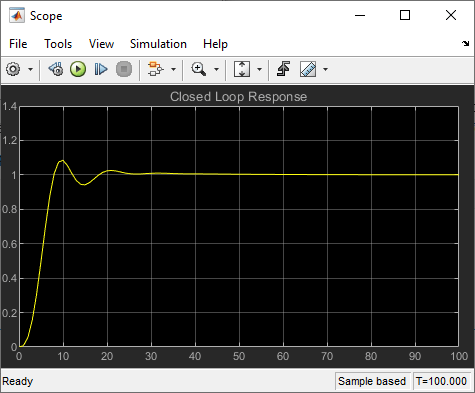
Kp = 3.1330

Ki = 0.1465

Kd = 14.3918

このスコープは、最適化された閉ループステップ応答を示しています。

lsqnonlin 後の閉ループ応答

メモ: sim を呼び出すことは結果的には Simulink の常微分方程式 (ODE) ソルバーの 1 つを呼び出すことになります。使用するソルバーのタイプを選択する必要があります。最適化という点から見ると、ODE が解けるのならば固定ステップ ODE ソルバーの選択が最良です。しかし、柔軟性のないシステムの場合には可変手順 ODE 法により ODE を解くことが必要になる場合があります。

しかし、可変ステップソルバーで求めた数値解は、ステップサイズ制御機能のためにパラメーターの平滑な関数ではありません。このような平滑性の欠如により、最適化ルーチンが収束しなくなる場合があります。固定ステップソルバーを使用した場合、平滑性の欠如が問題となることはありません。(詳細は [53] を参照)。

Simulink Design Optimization™ ソフトウェアは、Simulink の可変ステップソルバーと組み合わせて、多目的最適化問題を解決するために推奨されます。このソフトウェアを使用すると Simulink と連動して特殊な数値勾配計算を行い、平滑性の欠如の問題を回避します。

補助関数

次のコードは補助関数 runtracklsq を作成します。

function [Kp,Ki,Kd] = runtracklsq
% RUNTRACKLSQ demonstrates using LSQNONLIN with Simulink.
mdl = 'optsim';
open_system(mdl)                             % Load the model
in = Simulink.SimulationInput(mdl);          % Create simulation input object
in = in.setModelParameter('StopTime','100'); % Stop time 100
pid0 = [0.63 0.0504 1.9688];                 % Initial gain values
a1 = 3; a2 = 43;                             % Initialize model plant variables
options = optimoptions(@lsqnonlin,'Algorithm','levenberg-marquardt',...
   'Display','off','StepTolerance',0.001,'OptimalityTolerance',0.001);
% Optimize the gains
set_param(mdl,'FastRestart','on');           % Fast restart
pid = lsqnonlin(@tracklsq,pid0,[],[],options);
set_param(mdl,'FastRestart','off');
% Return the gains
Kp = pid(1); Ki = pid(2); Kd = pid(3); 

    function F = tracklsq(pid)
      % Track the output of optsim to a signal of 1
      % Set the simulation input object parameters
      in = in.setVariable('Kp',pid(1),'Workspace',mdl);
      in = in.setVariable('Ki',pid(2),'Workspace',mdl);
      in = in.setVariable('Kd',pid(3),'Workspace',mdl);
      
      % Simulate
      out = sim(in);
      F = out.get('yout') - 1;
    end
end

Simulink モデルでの lsqnonlin

補助関数

Simulink モデルでの `lsqnonlin`