fgoalattain を使用した信号処理
線形位相 Finite Impulse Response (FIR) フィルターの設計について考えてみます。問題とするのは、0 と 0.1 Hz 間の周波数帯域で振幅 1、0.15 と 0.5 Hz 間で振幅 0 となるローパス フィルターの設計です。
このようなフィルターの周波数応答 H(f) は次のように定義されます。
| (1) |
ここで、A(f) は周波数応答の大きさです。1つの解法は、ゴール到達法を周波数応答の大きさに適用するものです。大きさを計算する関数が与えられると、fgoalattain は大きさの応答がある許容誤差内で希望する応答と一致するまで大きさの係数 a(n) を変化させます。大きさの応答を計算する関数は filtmin.m で用意されています。この関数は、a (大きさの関数係数) と w (興味のある周波数領域の離散値) を使用します。
ゴール到達問題を設定するには、問題の goal と weights を指定しなければなりません。0 および 0.1 間の周波数に対して、ゴールは 1 です。0.15 および 0.5 間の周波数に対して、ゴールは 0 です。0.1 および 0.15 間の周波数に対しては、この範囲でゴールまたは重みを必要としないので指定しません。
この情報は変数 goal に保存され、fgoalattain に渡されます。goal の長さは関数 filtmin により戻される長さと同じです。複数のゴールが等価に満足されるためには、通常は weight を abs(goal) に設定します。しかし、ゴールのいくつかはゼロなので、weight=abs(goal) を使用することによって、weight 0 をもつ目的関数に厳しい制約を課すものになり、そして weight 1 をもつ目的関数がゴール値に到達しない可能性があります (ゴール到達法 を参照)。すべてのゴールは同じくらいの大きさであるので、すべてのゴールに weight を使用すると、ゴールに等しい優先順位を与えます。(重みに abs(goal) を使用すると、goal の大きさがより有意に異なるとき、重要性を増します。) また、以下のように設定すると
options = optimoptions('fgoalattain','EqualityGoalCount',length(goal));
各目的が可能な限りゴール値に近づく (超えることも小さくなることもない) ようになります。
手順 1: ファイル filtmin.m を記述する
function y = filtmin(a,w)
n = length(a);
y = cos(w'*(0:n-1)*2*pi)*a ;手順 2: 最適化ルーチンを呼び出す
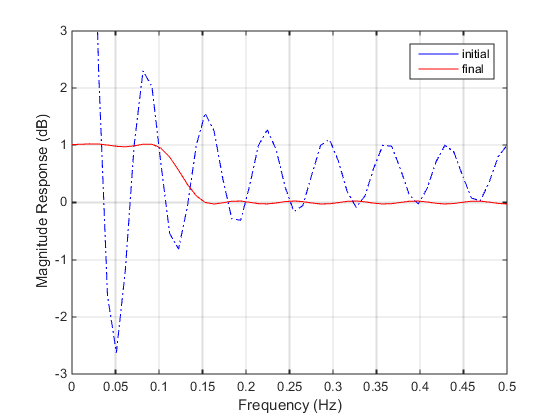
% Plot with initial coefficients a0 = ones(15,1); incr = 50; w = linspace(0,0.5,incr); y0 = filtmin(a0,w); clf, plot(w,y0,'-.b'); drawnow; % Set up the goal attainment problem w1 = linspace(0,0.1,incr) ; w2 = linspace(0.15,0.5,incr); w0 = [w1 w2]; goal = [1.0*ones(1,length(w1)) zeros(1,length(w2))]; weight = ones(size(goal)); % Call fgoalattain options = optimoptions('fgoalattain','EqualityGoalCount',length(goal)); [a,fval,attainfactor,exitflag]=fgoalattain(@(x)filtmin(x,w0),... a0,goal,weight,[],[],[],[],[],[],[],options); % Plot with the optimized (final) coefficients y = filtmin(a,w); hold on, plot(w,y,'r') axis([0 0.5 -3 3]) xlabel('Frequency (Hz)') ylabel('Magnitude Response (dB)') legend('initial', 'final') grid on
初期係数と最終的な係数で計算した振幅応答を比較してみてください (初期および最終の振幅係数をもつ振幅応答)。Signal Processing Toolbox™ 内の関数 firpm (Signal Processing Toolbox) を使用して、このフィルターを設計できることに注意してください。
初期および最終の振幅係数をもつ振幅応答