dist
角距離 (ラジアン)
説明
distance = dist(quatA,quatB)quatA と quatB 間の角距離 (ラジアン) を返します。
例
入力引数
出力引数
アルゴリズム
関数 dist は、2 つの四元数間の角距離を返します。
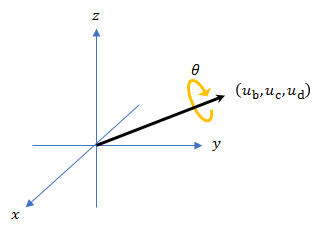
四元数は、回転の軸 (ub,uc,ud) および角度 θq によって として定義できます。
という形式の四元数が与えられた場合 (a は実数部)、角度 q は として解を求めることができます。
2 つの四元数 p と q、および積 について考えます。p が q に近づくにつれ、角度 z は 0 に近づき、z は単位四元数に近づきます。
2 つの四元数間の角距離は、 と表すことができます。
quaternion データ型構文を使用すると、角距離は次のように計算されます。
angularDistance = 2*acos(abs(parts(p*conj(q))));
拡張機能
バージョン履歴
R2019b で導入