最新のリリースでは、このページがまだ翻訳されていません。 このページの最新版は英語でご覧になれます。

median

配列の中央値

構文

M = median(A)

M = median(A,dim)

M = median(___,nanflag)

説明

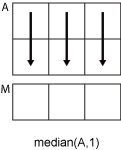
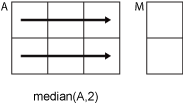
M = median(A) は、A の中央値を返します。

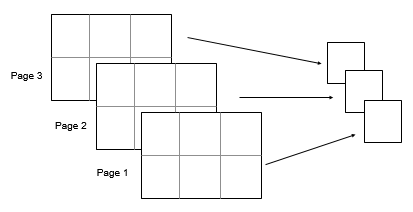
• A がベクトルの場合、median(A) は A の中央値を返します。

• A が空でない行列の場合、median(A) は A の列をベクトルとして取り扱い、中央値の行ベクトルを返します。

• A が空の 0 行 0 列の場合、median(A) は NaN を返します。

• A が多次元配列の場合、median(A) はサイズが 1 でない最初の配列次元に沿った値をベクトルとして扱います。この次元のサイズは 1 になりますが、他のすべての次元のサイズは変化しません。

median は、A の class(M) = class(A) などの数値クラスでネイティブに計算します。

M = median(A,dim) は、次元 dim に沿って要素の中央値を返します。たとえば、A が行列の場合、median(A,2) は各行の中央値をもつ列ベクトルになります。

M = median(___,nanflag) は、前述のすべての構文で中央値の計算に NaN 値を含めるか省略するかをオプションで指定します。たとえば、median(A,'omitnan') は A のすべての NaN 値を無視します。

例

行列の列の中央値

4 行 3 列の行列を定義します。

A = [0 1 1; 2 3 2; 1 3 2; 4 2 2]

A = 4×3

     0     1     1
     2     3     2
     1     3     2
     4     2     2

各列の中央値を求めます。

M = median(A)

M = 1×3

    1.5000    2.5000    2.0000

各列では、中央値は並べ替え順序になっている中間の 2 つの数値の平均です。

行列の行の中央値

2 行 3 列の行列を定義します。

A = [0 1 1; 2 3 2]

A = 2×3

     0     1     1
     2     3     2

各行の中央値を求めます。

M = median(A,2)

M = 2×1

     1
     2

各行では、中央値は並べ替え順序になっている中間の数値です。

3 次元配列の中央値

1 と 10 の間の整数の 1 x 3 x 4 の配列を作成します。

A = gallery('integerdata',10,[1,3,4],1)

A = 
A(:,:,1) =

    10     8    10


A(:,:,2) =

     6     9     5


A(:,:,3) =

     9     6     1


A(:,:,4) =

     4     9     5

2 番目の次元に沿って 3 次元配列の中央値を求めます。

M = median(A)

M = 
M(:,:,1) =

    10


M(:,:,2) =

     6


M(:,:,3) =

     6


M(:,:,4) =

     5

この演算は、2 番目の次元に沿って 3 つの値の中央値を計算することによって 1 x 1 x 4 の配列を生成します。2 番目の次元のサイズは 1 に縮小します。

A の最初の次元に沿って中央値を計算します。

M = median(A,1);
isequal(A,M)

ans = logical
   1

最初の次元のサイズは 1 なので、このコマンドは A と同じ配列を返します。

8 ビット整数配列の中央値

8 ビット整数の 1 行 4 列のベクトルを定義します。

A = int8(1:4)

A = 1x4 int8 row vector

   1   2   3   4

中央値を計算します。

M = median(A),

M = int8
    3

class(M)

ans = 
'int8'

M は、8 ビット整数として返された、並べ替え順序になっている中間の 2 つの数値の平均です。

NaN を除外した中央値

ベクトルを作成し、NaN 値を除いてその中央値を計算します。

A = [1.77 -0.005 3.98 -2.95 NaN 0.34 NaN 0.19];
M = median(A,'omitnan')

M = 0.2650

入力引数

A — 入力配列

ベクトル | 行列 | 多次元配列

入力配列。ベクトル、行列または多次元配列として指定します。A には数値配列、順序 categorical 配列、datetime 配列または duration 配列を使用できます。

dim — 演算の対象の次元

正の整数スカラー

演算の対象の次元。正の整数のスカラーとして指定します。値を指定しない場合、既定値は、サイズが 1 ではない最初の配列の次元です。

次元 dim は、長さが 1 に縮小した次元を示します。size(M,dim) は 1 ですが、他のすべての次元のサイズは変化しません。

2 次元の入力配列 A について考えます。

• dim = 1 の場合、median(A,1) は、各列の要素の中央値を含む行ベクトルを返します。

  

• dim = 2 の場合、median(A,2) は、各行の要素の中央値を含む列ベクトルを返します。

  

dim が ndims(A) より大きい場合、median は A を返します。

nanflag — NaN の条件

'includenan' (既定値) | 'omitnan'

NaN の条件。次の値のいずれかとして指定します。

• 'includenan' — NaN 値を含む入力の中央値は NaN です。

• 'omitnan' — 入力にあるすべての NaN 値が無視されます。メモ: NaN フラグは 0 に設定されません。

また、一部のデータ型については追加の値を指定することもできます。

• 'includeundefined' および 'omitundefined' — categorical 入力

• 'includenat' および 'omitnat' — datetime 入力

アルゴリズム

順序 categorical 配列の場合は、MATLAB^® は偶数個の要素の中央値を次のように解釈します。

2 つの中間の値の間にあるカテゴリの数 ...	中央値 ...
ゼロ (連続カテゴリの値)	2 つの中間値のうち大きい方
奇数	2 つの中間値の間に発生するカテゴリの値
偶数	2 つの中間値の間に発生する 2 つのカテゴリのうち大きい方の値

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

使用上の注意事項および制限事項:

最初の次元で median を計算するには、入力 A が列ベクトルでなければなりません。

詳細については、tall 配列を参照してください。

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• 指定する場合、dim は定数でなければなりません。

• ツールボックス関数のコード生成に対する可変サイズの制限 (MATLAB Coder)

• ゼロ値の虚数部をもつ複素数データのコード生成 (MATLAB Coder)

参考

corrcoef | cov | max | mean | min | mode | std | var

R2006a より前に導入