nearest

半径内の最近傍

構文

nodeIDs = nearest(G,s,d)

nodeIDs = nearest(G,s,d,Name,Value)

[nodeIDs,dist] = nearest(___)

説明

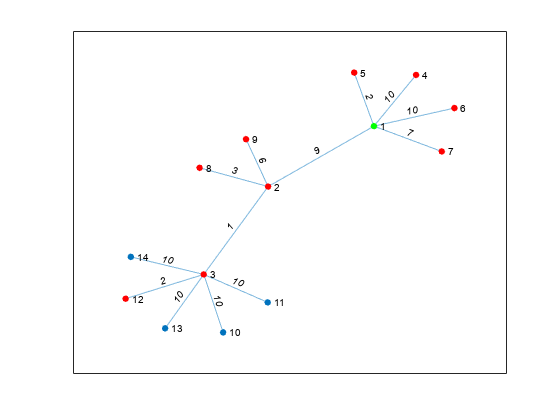
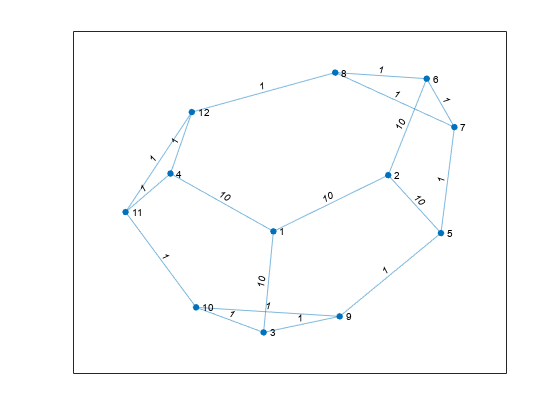
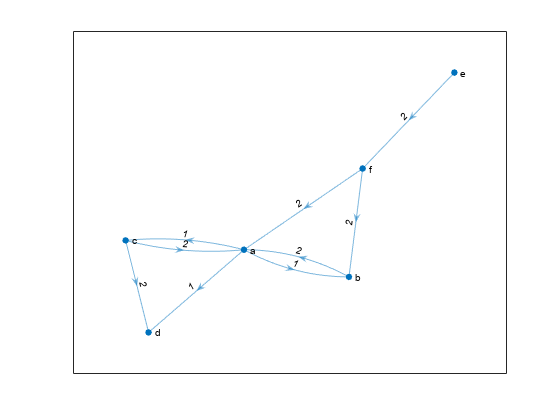
nodeIDs = nearest(G,s,d) は、グラフ G 内のノード s から距離 d 以内にあるすべてのノードを返します。グラフが重み付き (つまり、G.Edges が変数 Weight を含む) の場合、これらの重みはグラフ内のエッジの距離として使用されます。それ以外の場合、すべてのエッジの距離は 1 と見なされます。

nodeIDs = nearest(G,s,d,Name,Value) は、1 つ以上の名前と値のペアの引数で指定された追加のオプションを使用します。たとえば、G が重み付きグラフの場合、nearest(G,s,d,'Method','unweighted') はグラフ G のエッジの重みを無視し、すべてのエッジの重みを 1 として扱います。

[nodeIDs,dist] = nearest(___) はさらに、個々の最近傍までの距離を返します。dist(j) はソース ノード s からノード nodeIDs(j) までの距離です。前述の構文にある任意の入力引数の組み合わせが使用できます。

例

最も近いノード

重み付きエッジをもつグラフを作成し、プロットします。

s = [1 1 1 1 1 2 2 2 3 3 3 3 3];
t = [2 4 5 6 7 3 8 9 10 11 12 13 14];
weights = randi([1 10],1,13);
G = graph(s,t,weights);
p = plot(G,'Layout','force','EdgeLabel',G.Edges.Weight);

ノード 1 から半径 15 以内にどのノードがあるかを判定します。

nn = nearest(G,1,15)

nn = 9×1

     5
     7
     2
     3
     4
     6
     8
    12
     9

ソース ノードを緑、最近傍を赤で強調表示します。

highlight(p,1,'NodeColor','g')
highlight(p,nn,'NodeColor','r')

最も近いノードの距離

重み付きエッジをもつグラフを作成し、プロットします。

s = [1 1 1 2 2 6 6 7 7 3 3 9 9 4 4 11 11 8];
t = [2 3 4 5 6 7 8 5 8 9 10 5 10 11 12 10 12 12];
weights = [10 10 10 10 10 1 1 1 1 1 1 1 1 1 1 1 1 1];
G = graph(s,t,weights);
plot(G,'EdgeLabel',G.Edges.Weight)

ノード 3 から半径 5 以内にどのノードがあるかを判定し、各ノードまでの距離を返します。

[nn,dist] = nearest(G,3,5)

nn = 9×1

     9
    10
     5
    11
     4
     7
    12
     6
     8

dist = 9×1

     1
     1
     2
     2
     3
     3
     3
     4
     4

有向グラフにおける入方向の隣との距離

重み付きエッジをもつ有向グラフを作成し、プロットします。

s = {'a' 'a' 'a' 'b' 'c' 'c' 'e' 'f' 'f'};
t = {'b' 'c' 'd' 'a' 'a' 'd' 'f' 'a' 'b'};
weights = [1 1 1 2 2 2 2 2 2];
G = digraph(s,t,weights);
plot(G,'EdgeLabel',G.Edges.Weight)

ノード 'a' から出方向の経路の距離で測定した場合に、ノード 'a' から半径 1 以内にある最も近いノードを判定します。

nn_out = nearest(G,'a',1)

nn_out = 3x1 cell
    {'b'}
    {'c'}
    {'d'}

半径を Inf に指定して、ノード 'a' に至る入方向の経路をもつすべてのノードを判定します。

nn_in = nearest(G,'a',Inf,'Direction','incoming')

nn_in = 4x1 cell
    {'b'}
    {'c'}
    {'f'}
    {'e'}

入力引数

G — 入力グラフ

graph オブジェクト | digraph オブジェクト

入力グラフ。graph オブジェクトまたは digraph オブジェクトとして指定します。無向グラフの作成には graph を、有向グラフの作成には digraph を使用します。

例: G = graph(1,2)

例: G = digraph([1 2],[2 3])

s — ソース ノード

ノード インデックス | ノード名

ソース ノード。ノード インデックスまたはノード名として、次の表のいずれかの形式で指定します。

値	例
スカラー ノード インデックス	1
文字ベクトルのノード名	'A'
string スカラーのノード名	"A"

例: nearest(G,3,1)

例: nearest(G,'a',5)

d — 近傍距離の半径

スカラー

近傍距離の半径。数値スカラーとして指定します。

例: nearest(G,3,1)

例: nearest(G,'a',2.5)

名前と値の引数

引数のオプションのペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後になければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、コンマを使用してそれぞれの名前と値を区切り、Name を引用符で囲みます。

例: [nodeIDs,dist] = nearest(G,s,5,'Method','unweighted','Direction','incoming')

Direction — 距離測定の方向

'outgoing' (既定値) | 'incoming'

メモ

'Direction' オプションは、有向グラフにのみ指定できます。

距離測定の方向。'Direction' と、次の表のいずれかのオプションで構成されるコンマ区切りのペアとして指定します。

オプション	説明
'outgoing' (既定)	ソース ノード s から "出る" 経路を使用して、距離が計算されます。
'incoming'	ソース ノード s に "入る" 経路を使用して、距離が計算されます。

例: nearest(G,s,d,'Direction','incoming')

Method — 最短経路アルゴリズム

'auto' (既定値) | 'unweighted' | 'positive' | 'mixed'

最短経路アルゴリズム。'Method' と、次の表のいずれかのオプションで構成されるコンマ区切りのペアとして指定します。

オプション	説明
'auto' (既定)	'auto' オプションを設定すると、自動的にアルゴリズムが選択されます。 'unweighted' は、エッジの重みをもたない graph および digraph の入力に対して使用されます。 'positive' はエッジの重みをもつすべての graph の入力に対して使用され、重みは非負の数であることが求められます。このオプションは、エッジの重みが非負である digraph の入力に対しても使用されます。 'mixed' は、一部のエッジの重みに負数が含まれる digraph の入力に対して使用されます。グラフは負の循環をもつことができません。
'unweighted'	幅優先検索。すべてのエッジの重みを 1 として扱います。
'positive'	ダイクストラ アルゴリズム。すべてのエッジの重みが非負の数でなければなりません。
'mixed' (digraph 専用)	有向グラフのベルマン・フォード アルゴリズム。グラフに負の循環があってはなりません。 同じ問題について 'mixed' の処理速度は 'positive' よりも遅くなりますが、'mixed' は一部のエッジに負の重みを使用できるので、より柔軟です。

メモ

多くのグラフについて、'unweighted' が最速のアルゴリズムであり、次に 'positive'、'mixed' の順になっています。

例: nearest(G,s,d,'Method','positive')

出力引数

nodeIDs — 最近傍のノード ID

ノード インデックス | ノード名

最近傍のノード ID。s が数値である場合はノード インデックス、s がノード名である場合はノード名として返されます。ノードは最も近いものから遠いものへと並べ替えられます。指定距離内にノードが存在しない場合、nodeIDs は空になります。グラフに自己ループがある場合でも、nodeIDs にソース ノード s が含まれることはありません。

元のグラフ G から最近傍の部分グラフを抽出するには、H = subgraph(G,[s; nodeIDs]) を使用します。

dist — 隣への距離

ベクトル

隣への距離。ベクトルとして返されます。dist(j) は、ソース ノード s から隣接ノード nodeIDs(j) までの距離です。

拡張機能

C/C++ コード生成

MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

• 名前と値の引数は定数でなければなりません。

• 'positive'、'unweighted' および 'auto' のメソッドのみがサポートされています。

バージョン履歴

R2016a で導入

参考

shortestpath | distances | shortestpathtree | neighbors | successors | predecessors

トピック

• graph
• digraph

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい