nufft
非等間隔高速フーリエ変換
説明
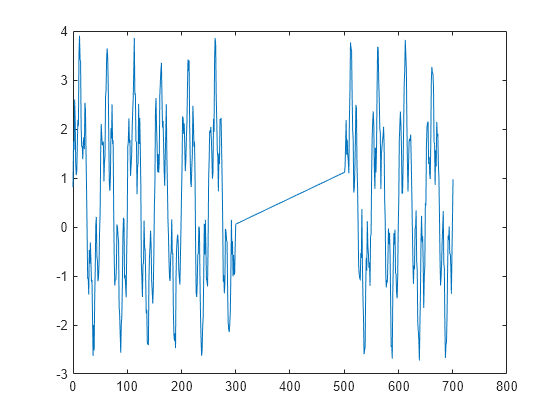
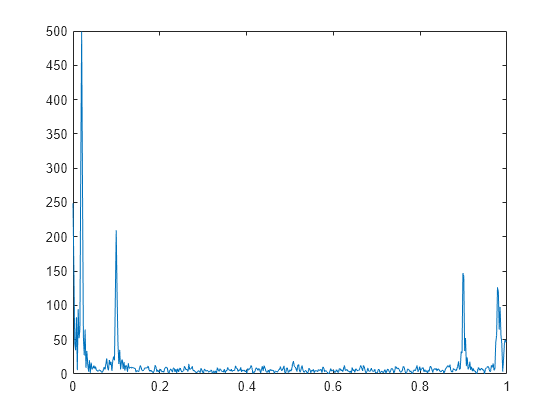
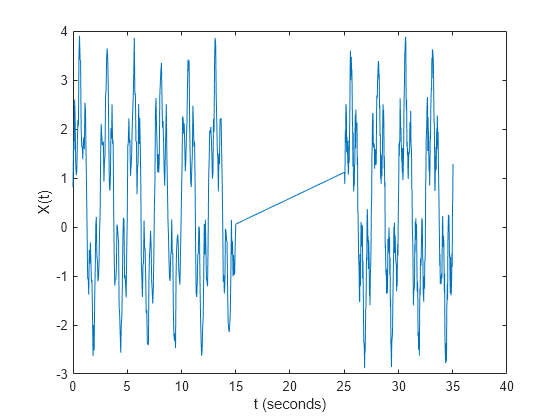
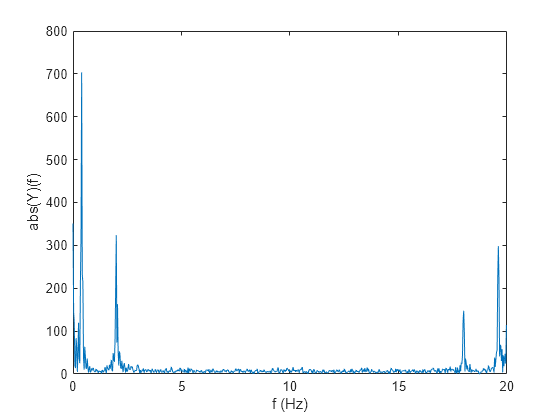
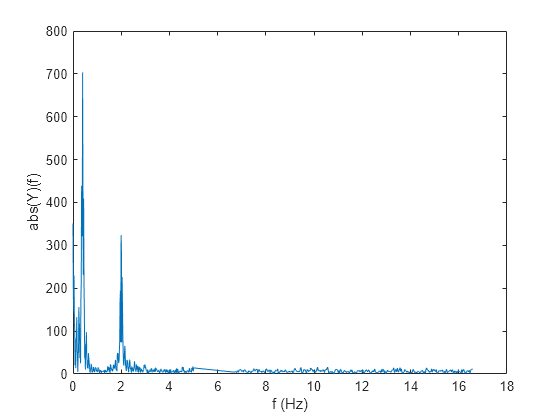
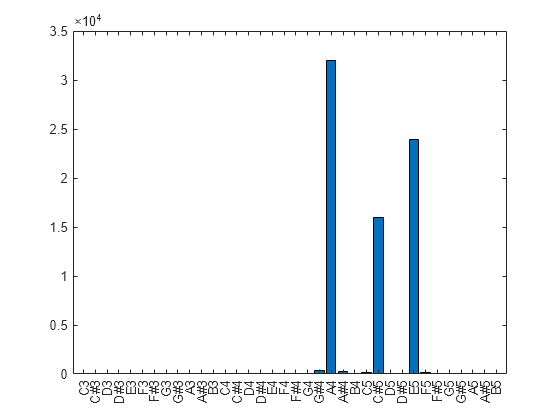
Y = nufft(X,t)t を使用した X の非等間隔離散フーリエ変換 (NUDFT) を返します。
Xがベクトルの場合、nufftはそのベクトルの変換を返します。Xが行列の場合、nufftは、Xの列をベクトルとして扱い、各列の変換を返します。Xが多次元配列の場合、nufftは、サイズが 1 ではない最初の配列次元に沿った値をベクトルとして扱い、各ベクトルの変換を返します。
Y = nufft(X)X の離散フーリエ変換を返します。これは fft(X) と等価です。
例
等間隔でない点 t でサンプリングされた信号 X を作成します。信号をプロットします。
t = [0:300 500.5:700.5]; S = 2*sin(2*pi*0.02*t) + sin(2*pi*0.1*t); X = S + rand(size(t)); plot(t,X)
信号の非等間隔高速フーリエ変換を求めます。3 番目の引数に周波数を指定せずに nufft を使用すると、nufft は、n の信号長に対して周波数が f(i) = (i-1)/n の形式をとる既定の周波数スケーリングを使用します。変換の絶対値を既定の周波数の関数としてプロットします。
Y = nufft(X,t); n = length(t); f = (0:n-1)/n; plot(f,abs(Y))
非等間隔サンプル点の時間ベクトルを作成します。等間隔にサンプリングされた等価のデータに対して、サンプリング周期 T = 50 ms (またはサンプリング周波数 Fs = 20 Hz) で約 35 秒の期間を定義します。
T = 50e-3; % Sampling period of 50 ms for equivalent uniform samples Fs = 1/T; % Sampling frequency of 20 Hz for equivalent uniform samples t = [0:T:300*T 500.5*T:T/2:700.5*T];
0.4 Hz と 2 Hz にピーク周波数をもつ等間隔でない点 t でサンプリングされた信号 X を作成します。
S = 2*sin(2*pi*0.4*t) + sin(2*pi*2*t); % Signal with peak frequencies at 0.4 Hz and 2 Hz X = S + rand(size(t)); plot(t,X) xlabel("t (seconds)") ylabel("X(t)")
信号の非等間隔高速フーリエ変換を求めます。3 番目の引数に周波数を指定せずに nufft を使用します。この場合、nufft は、n の信号長に対して f(i) = (i-1)/n の形式をとる既定の周波数を使用します。非等間隔離散フーリエ変換は、非等間隔サンプル点 t と周波数 f を、等間隔にサンプリングされた等価のデータに対してサンプリング周期が 1 秒、サンプリング周波数が 1 Hz であるかのように扱います。このため、nufft を使用して正しくスケーリングされた単位で変換を求めるには、時間ベクトルにスケーリング係数 T を含めます。変換の絶対値を、Fs でスケーリングされた既定の周波数の関数としてプロットします。
Y = nufft(X,t/T); n = length(t); f = (0:n-1)/n*Fs; plot(f,abs(Y)) xlabel("f (Hz)") ylabel("abs(Y)(f)")
nufft を使用する場合は、3 番目の引数として非等間隔周波数ベクトルまたはクエリ点 f、2 番目の引数として非等間隔時間ベクトル t を指定することもできます。ここで、nufft を使用する場合は、t と f を再スケーリングする必要はありません。変換の絶対値を非等間隔周波数の関数としてプロットします。
f = [0:0.5:n/4 n/3+1:n-120]/n*Fs; Y = nufft(X,t,f); plot(f,abs(Y)) xlabel("f (Hz)") ylabel("abs(Y)(f)")
楽音の範囲の周波数を定義しラベル付けします。
C3 = 440 / (2^(21/12)); nOctaves = 3; musicalTones = C3 * 2.^((0:(12*nOctaves-1))/12); toneNames = ["C";"C#";"D";"D#";"E";"F";"F#";"G";"G#";"A";"A#";"B"] + string(3:(3+nOctaves-1)); toneNames = categorical(toneNames, toneNames);
音声信号のサンプリング周波数 (Hz)、サンプル点 n、およびメジャー コード X を含む信号を定義します。
fs = 16e3; n = 1:16000; X = 4*cos(2*pi*(440/fs)*n) + 2*cos(2*pi*(554.37/fs)*n) + 3*cos(2*pi*(659.2/fs)*n);
メジャー コードの周波数成分を計算しプロットします。
Y = nufft(X,[],musicalTones/fs); bar(toneNames(:),abs(Y))
入力引数
詳細
参照
[1] Potter, Samuel F., Nail A. Gumerov, and Ramani Duraiswami. “Fast Interpolation of Bandlimited Functions.” In 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 4516–20. New Orleans, LA: IEEE, 2017. https://doi.org/10.1109/ICASSP.2017.7953011.
[2] Dutt, A., and V. Rokhlin. “Fast Fourier Transforms for Nonequispaced Data.” SIAM Journal on Scientific Computing 14, no. 6 (November 1993): 1368–93. https://doi.org/10.1137/0914081.
拡張機能
バージョン履歴
R2020a で導入
