ライブ エディターを使用した対話型の表現の作成
ライブ エディターで対話型の表現を作成する方法の例を以下に示します。対話型の表現により、問題を解くのに使用する各計算を結び付けます。この例では、以下の操作方法を説明します。
出力を MATLAB® コードとともに表示する。
書式設定されたテキストを使用してアプローチを説明する。
数式を使用して基本となる計算を説明する。
イメージを使用して重要な点を図示する。
参考資料へのリンクを追加する。
コントロールを使用してパラメーターを変更し、解析を再実行する。
データをプロットして可視化する。
同僚と一緒に解析を拡張する。
全体的なアプローチ
書式設定したテキストを対話型の表現の一部として含めます。重要な単語を強調表示するには、太字、イタリック、および下線付きテキストを使用します。リストの書式設定には、黒丸や番号を使用します。
以下を計算することにより、一般的なソーラー パネル装置からの特定の日時と場所における "電力出力" を推定します。
太陽時
赤緯と太陽高度
エア マスと地表に到達する太陽放射
位置、傾きおよび効率性が与えられた場合のソーラー パネルでの放射
1 日および 1 年間の発電量
これらの計算の結果を使用して、例の日付と場所での太陽放射とパネル放射をプロットします。その後、1 年間を通じて予測されるパネルの発電量をプロットします。解析を効率化するために、この例用に作成された 2 つの MATLAB 関数 solarCorrection および panelRadiation を使用します。
太陽時
出力をその生成元コードとともに表示します。コードのセクションを実行するには、[ライブ エディター] タブに移動し、[セクションの実行] ボタンをクリックします。
ソーラー パネルでの発電量は、パネルに到達する太陽放射量によって決まります。またこれは、太陽が空を移動するときの、パネルに対する太陽の位置に応じて異なります。たとえば、6 月 1 日正午 12 時のマサチューセッツ州ボストンにおけるソーラー パネルの電力出力を計算するとします。
lambda =-71.06; % longitude phi =
42.36; % latitude UTCoff =
'-5'; % UTC offset january1 = datetime(2019,1,1); % January 1st localTime = datetime(2019,6,1,12,0,0) % Noon on June 1
localTime = datetime
01-Jun-2019 12:00:00
特定の日時における太陽の位置を計算するには、"太陽時" を使用します。太陽時の正午 12 時は、太陽が空の最も高い位置にある時刻です。太陽時を計算するために、現地時間に補正を適用します。この補正には次の 2 つの部分があります。
観察者の位置と現地の子午線間の差を補正する項
地球の軌道離心率と自転軸の傾きに関連する軌道項
関数 solarCorrection を使用して太陽時を計算します。
d = caldays(between(january1,localTime,'Day')); % Day of year solarCorr = solarCorrection(d,lambda,str2double(UTCoff)); % Correction to local time solarTime = localTime + minutes(solarCorr)
solarTime = datetime
01-Jun-2019 12:18:15
赤緯と太陽高度
基本となる計算を記述する数式を含めます。LaTeX コマンドを使用して数式を作成します。新しい数式を追加するには、[挿入] タブに移動し、[式] ボタンをクリックします。数式をダブルクリックし、数式エディターで編集します。
赤緯 () は、地球の赤道面に対する太陽の角度です。赤緯は春分と秋分に となり、夏至に最大値の まで上昇します。次の数式を使用して、特定の年間通算日 (d) の赤緯を計算します。
次に、赤緯 ()、緯度 ()、および時角 () を使用して、現在の時刻の太陽高度 () を計算します。時角とは、現在の太陽時と太陽正午間の地球の自転角度です。
delta = asind(sind(23.45)*sind(360*(d - 81)/365)); % Declination omega = 15*(solarTime.Hour + solarTime.Minute/60 - 12); % Hour angle alpha = asind(sind(delta)*sind(phi) + ... % Elevation cosd(delta)*cosd(phi)*cosd(omega)); disp(['Solar Declination = ' num2str(delta) ' Solar Elevation = ' num2str(alpha)])
Solar Declination = 21.8155 Solar Elevation = 69.113
太陽の赤緯と現地の緯度を使用して、標準時での日の出と日没の時刻を計算します。
midnight = dateshift(localTime,'start','day'); sr = 12 - acosd(-tand(phi)*tand(delta))/15 - solarCorr/60; sunrise = timeofday(midnight + hours(sr)); ss = 12 + acosd(-tand(phi)*tand(delta))/15 - solarCorr/60; sunset = timeofday(midnight + hours(ss)); sunrise.Format = 'hh:mm:ss'; sunset.Format = 'hh:mm:ss'; disp('Sunrise = ' + string(sunrise) + ' Sunset = ' + string(sunset))
Sunrise = 04:16:06 Sunset = 19:07:22
エア マスと太陽放射
解説における重要な点を図示するためにイメージを含めます。イメージを含めるには、別のソースからイメージをコピーして貼り付けるか、[挿入] タブに移動して [イメージ] ボタンをクリックします。
太陽からの光が地球の大気圏を通過するときに、一部の太陽放射が吸収されます。エア マスは、以下の図に示すように太陽の仰角が 90 である場合の最短の経路 (X) に対する、大気圏を通過する光の経路長 (Y) です。これは太陽の仰角 () の関数です。
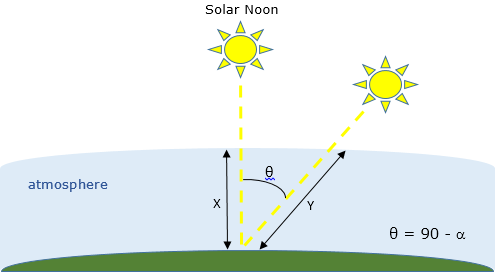
エア マスが大きいほど、地上に到達する放射量は少なくなります。次の数式を使用してエア マスを計算します。
次に、経験式を使用して、地上に到達する太陽放射量 (キロワット毎平方メートル単位) を計算します。
airMass = 1/(cosd(90-alpha) + 0.50572*(6.07955+alpha)^-1.6354); solarRad = 1.353*0.7^(airMass^0.678); % kW/m^2 disp(['Air Mass = ' num2str(airMass) ' Solar Radiation = ' num2str(solarRad) ' kW/m^2'])
Air Mass = 1.0698 Solar Radiation = 0.93141 kW/m^2
固定パネルへの太陽放射
ハイパーリンクを使用して他のソースからのサポート情報を参照します。ハイパーリンクを追加するには、[挿入] タブに移動して、[ハイパーリンク] ボタンをクリックします。
太陽光追尾装置が設置されているパネルは太陽の動きに合わせて移動し、太陽が空を移動するときの太陽の放射を 100% 受けることができます。しかし、ほとんどの太陽電池装置では、パネルの方位角と傾きは固定されています。したがって、パネルに到達する実際の放射量は太陽の方位角によっても異なります。太陽の方位角 () は、空における太陽の位置のコンパス方位です。北半球では、太陽正午に太陽の方位角が になり、これは南の方角に対応します。次の式を使用して太陽の方位角を計算します。
gamma = acosd((sind(delta)*cosd(phi) - cosd(delta)*sind(phi)*cosd(omega))/cosd(alpha)); if (hour(solarTime) >= 12) && (omega >= 0) gamma = 360 - gamma; end disp(['Solar Azimuth = ' num2str(gamma)])
Solar Azimuth = 191.7888
北半球にある標準的なソーラー パネル装置には、パネル方位角 () が の南向きのパネルが取り付けられています。北緯における標準的な傾斜角 () は です。次の数式を使用して、固定パネルのパネル放射を合計太陽放射から計算します。
.
beta = 180; % Panel azimuth tau = 35; % Panel tilt panelRad = solarRad*max(0,(cosd(alpha)*sind(tau)*cosd(beta-gamma) + sind(alpha)*cosd(tau))); disp(['Panel Radiation = ' num2str(panelRad) ' kW/m^2'])
Panel Radiation = 0.89928 kW/m^2
1 日のパネル放射と発電量
対話型コントロールを使用してパラメーターを変更します。プロットをその生成元コードとともに表示します。
パネル放射
特定の年間通算日について、合計太陽放射とパネルへの放射を計算します。解析を単純化するため、関数 panelRadiation を使用します。さまざまな日付を試して、太陽放射とパネル放射が時期によってどのように変化するかを確認します。
selectedMonth =6; selectedDay =
1; selectedDate = datetime(2019,selectedMonth,selectedDay); [times,solarRad,panelRad] = panelRadiation(selectedDate,lambda,phi,UTCoff,tau,beta) ; plot(times,solarRad,times,panelRad) selectedDate.Format = 'MMMM dd yyyy'; title('Solar and Panel Radiation for ' + string(selectedDate)) xlabel('Hour of Day'); ylabel('Radiation, kW/m^2') legend('Available Solar Radiation','Solar Radiation on Panel', 'Location','South')
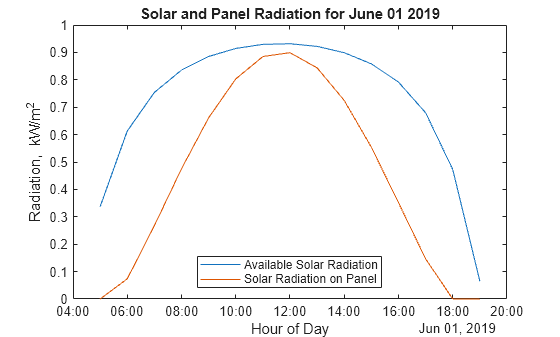
発電量
これまでの計算では、パネルに到達する放射はすべて発電に利用できると想定されていました。しかし、ソーラー パネルは使用可能な太陽放射を 100% 電気に変換するわけではありません。ソーラー パネルの効率性は、利用可能な放射が電気に変換される割合です。ソーラー パネルの効率性は、太陽電池の設計と材料によって異なります。
一般的に、住宅用装置には効率が 25% のソーラー パネルが 20 備えられています。以下のパラメーターを変更して、効率性とサイズがパネルでの発電にどのように影響するかを確認します。
eff =0.25; % Panel efficiency pSize =
20; % Panel size in m^2 radiation = sum(panelRad(1:end-1)+panelRad(2:end))/2; dayPower = eff*pSize*radiation; % Panel electric output in kW selectedDate.Format = 'dd-MMM-yyyy'; disp('Expected daily electical output for ' + string(selectedDate) + ' = ' + num2str(dayPower) + ' kW')
Expected daily electical output for 01-Jun-2019 = 33.4223 kW
1 年間の発電量
プロットを操作するには、その上にカーソルを合わせます。ライブ エディターでプロットを操作するとコードが生成され、後でスクリプトに追加することができます。
計算を繰り返して、各年間通算日の発電量を推定します。
yearDates = datetime(2019,1,1:365); % Create a vector of days in the year dailyPower = zeros(1,365); for i = 1:365 [times,solarRad,panelRad] = panelRadiation(yearDates(i),lambda,phi,UTCoff,tau,beta) ; radiation = sum(panelRad(1:end-1)+panelRad(2:end))/2; dailyPower(i) = eff*pSize*radiation; end plot(yearDates,dailyPower) title('Yearly Power Generation') xlabel('Date'); ylabel('Power Generation, kW')

yearlyPower = sum(dailyPower); disp(['Expected annual power output = ' num2str(yearlyPower) ' kW'])
Expected annual power output = 9954.3272 kW
パネルの傾きと緯度
ヒートマップを使用して、パネルの傾きが発電量にどのように影響するかを判定します。以下のヒートマップは、任意の位置での最適なパネルの傾きは、緯度より約 小さいことを示しています。
load LatitudeVsTilt.mat heatmap(powerTbl,'Tilt','Latitude',... 'ColorVariable','Power'); xlabel('Panel Tilt') ylabel('Latitude') title('Normalized Power Output')

解析の拡張
解析内容を同僚と共有します。同僚と一緒に解析を再現したり、その解析を拡張したりします。ライブ エディターを使用して共同作業します。
現実には、ソーラー装置からの実際の電力出力は、現地の天候状況に大きく影響を受けます。この解析を拡張して、雲量が結果に与える影響を確認してみるのもよいでしょう。米国では、次の行政機関の Web サイトのデータを使用できます。
National Weather Service Web サイトの過去の現地天候データ。
National Solar Radiation Database の太陽放射の測定データ。