スカラー関数の根
1 変数の非線形方程式の求解
関数fzeroは、1 変数の方程式の根を探索します。この関数は、1 要素の初期点または初期区間を設定する 2 要素ベクトルのいずれかで呼び出すことができます。関数 fzero に初期値 x0 を指定すると、関数 fzero はこの点の周辺で符号の変わる区間を最初に探索します。区間が見つかると、関数 fzero から関数値の符号が変わる場所の近傍の値が返されます。この区間が見つからない場合、関数 fzero は NaN を返します。また関数値の符号が変化する 2 点が既にわかっている場合は、2 要素ベクトルを使ってこの初期区間を指定できます。関数 fzero はこの区間を狭く絞り込み、符号の変化する近傍の値を返します。
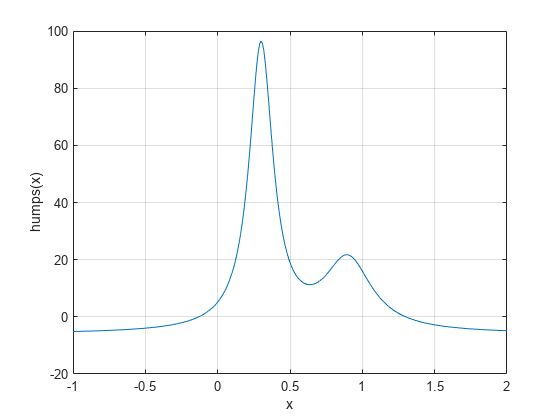
次の節では、初期区間と初期点を使って関数のゼロ点を見つける方法を説明する 2 つの例を示します。例では、MATLAB® に提供されている関数 humps.m を使用します。次の図は humps のグラフを示しています。
x = -1:.01:2; y = humps(x); plot(x,y) xlabel('x'); ylabel('humps(x)') grid on
fzero のオプション設定
オプションを設定することで、関数 fzero をいくつかの面で制御することができます。optimsetを使用してオプションを設定します。オプションは次のとおりです。
fzeroが生成する表示の量を選択する — 最適化オプションの設定、初期区間の使用、および初期点の利用を参照してください。fzeroが根の位置にあるか判定する方法を制御するさまざまな許容誤差を選択する — 最適化オプションの設定を参照してください。根に向かう
fzeroの進行状況を観測するためのプロット関数を選択する — 最適化ソルバーのプロット関数を参照してください。根に向かう
fzeroの進行状況を観測するための、カスタム プログラムされた出力関数を使用する — 最適化ソルバーの出力関数を参照してください。
初期区間の使用
humps のグラフは、関数が x = -1 で負となり x = 1 で正となることを示しています。これは、これら 2 点で humps を計算することにより確認できます。
humps(1)
ans = 16
humps(-1)
ans = -5.1378
したがって、関数 fzero に対する初期区間として [-1 1] が使用できます。
fzero の反復アルゴリズムは、[-1 1] の部分区間を徐々に小さくしていきます。各部分区間では、humps の符号が 2 つの端点で異なっています。部分区間の端点が互いに近付いていくと、humps のゼロ点に収束します。
各反復での fzero の進行状況を表示するには、関数optimsetを使用して、iter に Display オプションを設定します。
options = optimset('Display','iter');
そして、次のように関数 fzero を呼び出します。
a = fzero(@humps,[-1 1],options)
Func-count x f(x) Procedure
2 -1 -5.13779 initial
3 -0.513876 -4.02235 interpolation
4 -0.513876 -4.02235 bisection
5 -0.473635 -3.83767 interpolation
6 -0.115287 0.414441 bisection
7 -0.115287 0.414441 interpolation
8 -0.132562 -0.0226907 interpolation
9 -0.131666 -0.0011492 interpolation
10 -0.131618 1.88371e-07 interpolation
11 -0.131618 -2.7935e-11 interpolation
12 -0.131618 8.88178e-16 interpolation
13 -0.131618 8.88178e-16 interpolation
Zero found in the interval [-1, 1]
a = -0.1316
各値 x は、それまでの最良の端点を表します。Procedure は、アルゴリズムの各ステップが 2 分法と内挿法のどちらを使用しているかを示しています。
a の関数値が 0 に近いことは、次のように入力することで確認することができます。
humps(a)
ans = 8.8818e-16
初期点の利用
humps の関数値の符号が異なる 2 つの点が、未知であると仮定します。この場合、関数 fzero の初期点としてスカラー x0 を選択することができます。関数 fzero は、まず初期点周辺で両端での humps 関数の値の符号が異なる区間を探します。関数 fzero がその区間を検出すると、前の節で説明したアルゴリズムを使用して計算します。この区間が見つからない場合、関数 fzero は NaN を返します。
たとえば、開始点を -0.2、Display オプションを Iter に設定して、次のように関数 fzero を実行します。
options = optimset('Display','iter'); a = fzero(@humps,-0.2,options)
Search for an interval around -0.2 containing a sign change:
Func-count a f(a) b f(b) Procedure
1 -0.2 -1.35385 -0.2 -1.35385 initial interval
3 -0.194343 -1.26077 -0.205657 -1.44411 search
5 -0.192 -1.22137 -0.208 -1.4807 search
7 -0.188686 -1.16477 -0.211314 -1.53167 search
9 -0.184 -1.08293 -0.216 -1.60224 search
11 -0.177373 -0.963455 -0.222627 -1.69911 search
13 -0.168 -0.786636 -0.232 -1.83055 search
15 -0.154745 -0.51962 -0.245255 -2.00602 search
17 -0.136 -0.104165 -0.264 -2.23521 search
18 -0.10949 0.572246 -0.264 -2.23521 search
Search for a zero in the interval [-0.10949, -0.264]:
Func-count x f(x) Procedure
18 -0.10949 0.572246 initial
19 -0.140984 -0.219277 interpolation
20 -0.132259 -0.0154224 interpolation
21 -0.131617 3.40729e-05 interpolation
22 -0.131618 -6.79505e-08 interpolation
23 -0.131618 -2.98428e-13 interpolation
24 -0.131618 8.88178e-16 interpolation
25 -0.131618 8.88178e-16 interpolation
Zero found in the interval [-0.10949, -0.264]
a = -0.1316
各反復における現時点での部分区間の端点は、見出し a、b の下に挙げられています。端点に対応する関数 humps の値は、それぞれ f(a) と f(b) の下に挙げられています。
メモ: 端点 a と端点 b は、特定の順序で記載されてはいません。a が b より大きい場合もあれば、b より小さい場合もあります。
最初の 9 ステップにおいて、humps の符号は各時点の部分区間の両端で負となり、これは出力に示されています。ステップ 10 で、humps の値の符号は a (-0.10949) で正となり、b (-0.264) で負となります。この先アルゴリズムは、前節で説明したように、-0.1316 に到達するまで区間 [-0.10949 -0.264] を引き続き狭めていきます。