球内の乱数

この例では、Knuth [1] の記述に従って、球内を範囲とする乱数の点を作成する方法を示します。この例の球の中心は原点で、半径は 3 です。

球内の点を作成する 1 つの方法は、それらを球面座標で指定することです。その後、直交座標に変換してプロットすることができます。

まず、乱数発生器を初期化してこの例の結果を再現可能にします。

rng(0,'twister')

球内の各点の仰角を計算します。これらの値は開区間 $\left(-\pi /2,\pi /2\right)$ にありますが、一様分布していません。

rvals = 2*rand(1000,1)-1;
elevation = asin(rvals);

球内の各点の方位角を作成します。これらの値は開区間 $$(0,2\pi )$$ で一様分布しています。

azimuth = 2*pi*rand(1000,1);

球内の各点の半径値を作成します。これらの値は開区間 $$(0,3)$$ にありますが、一様分布していません。

radii = 3*(rand(1000,1).^(1/3));

直交座標に変換し、結果をプロットします。

[x,y,z] = sph2cart(azimuth,elevation,radii);
figure
plot3(x,y,z,'.')
axis equal

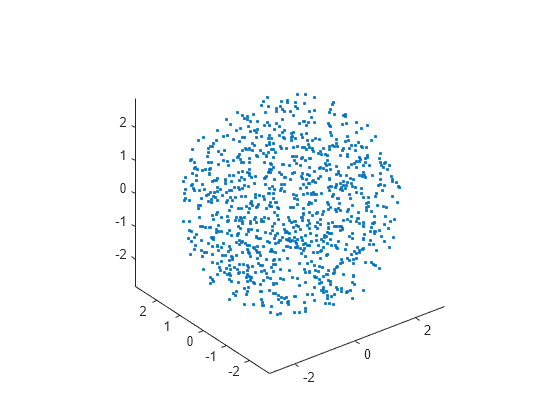
球の "表面上" に乱数を配置する場合は、sph2cart の最後の入力引数として定数の半径値を指定します。ここでは、値を 3 にしています。

[x,y,z] = sph2cart(azimuth,elevation,3);

参考

rng | rand | sph2cart

トピック

• 指定範囲内の乱数
• 指定の平均値と分散をもつ正規分布からの乱数
• 乱数配列の作成