このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

複素数のプロット

この例では、MATLAB® で複素数をプロットする方法を示します。複素数 $$z$$ は、次の形式で記述できる数です。

$\mathit{z}=\mathit{x}+\mathit{y}\mathrm{i}$,

ここで、$$x$$ と $$y$$ は実数であり、$$i$$ は虚数単位で、$$i^2=-1$$ と定義されます。数 $$x$$ は複素数の実数部であり、$$x=Re(z)$$ で表されます。また、数 $$y$$ は複素数の虚数部であり、$$y=Im(z)$$ で表されます。複素数は、複素平面上に座標のペア $$(x,y)$$ としてプロットできます。これはアルガン図とも呼ばれます。この図では、直交座標を使用して、実数部を $$x$$ 軸に、虚数部を $$y$$ 軸に表します。

複素数は極座標表現を使用して表すこともできます。複素数は次の形式で記述されます。

$\mathit{z}=\mathit{r}{\mathit{e}}^{\mathit{i}\theta }=\mathit{r}\left(\cos \theta +\mathrm{i}\sin \theta \right)$,

ここで、$$r$$ は複素数の絶対値 (大きさ) であり、$$\theta$$ は複素数の位相角です。この表現では、半径 $$r$$ (原点からの距離)、極角 $$\theta$$ (正の実数軸から点と原点を結ぶ線までの反時計回りの角度) の極座標の点として複素数をプロットできます。

複素数の配列のプロット

複素数 3 + 4i、-4 - 3i、1 - 2i、および -1 - 1i を含むベクトルを作成します。

z = [3 + 4i; -4 - 3i; 1 - 2i; -1 - 1i]

z = 4×1 complex

   3.0000 + 4.0000i
  -4.0000 - 3.0000i
   1.0000 - 2.0000i
  -1.0000 - 1.0000i

plot を使用して、複素数ベクトル z の虚数部と実数部をプロットします。複素数ベクトルの実数部と虚数部を返すには、それぞれ real 関数と imag 関数を使用します。

plot(real(z),imag(z),"o")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

plot(real(z),imag(z),LineSpec) の代わりに plot(z,LineSpec) を使用して複素数の配列をプロットすることもできます。この関数は、実数部を $$x$$ 軸、虚数部を $$y$$ 軸として自動的にプロットします。

直交座標における 1 の複素根のプロット

1 の $$n$$ 乗根は、次の多項方程式を満たす複素数です。

${\mathit{z}}^{\mathit{n}}=1$,

ここで、$$n$$ は正の整数です。

1 の $$n$$ 乗根は次のとおりです。

$\exp \left(\frac{2\mathit{k}\pi \mathrm{i}}{\mathit{n}}\right)=\cos \frac{2\mathit{k}\pi }{\mathit{n}}+\mathrm{i}\sin \frac{2\mathit{k}\pi }{\mathit{n}}$ (ただし、$\mathit{k}=0,1,\dots ,\mathit{n}-1$)

1 の複素根を求めるには、roots を使用して多項方程式を解きます。roots 関数は、${\mathit{p}}_1{\mathit{x}}^{\mathit{n}}+\cdots +{\mathit{p}}_{\mathit{n}}\mathit{x}+{\mathit{p}}_{\mathit{n}+1}=0$ という形式の多項方程式を解きます。たとえば、1 の 5 乗根 ($$z^5=1$$、すなわち $$z^5-1=0$$) を求めます。

p = [1 0 0 0 0 -1];
z = roots(p)

z = 5×1 complex

  -0.8090 + 0.5878i
  -0.8090 - 0.5878i
   0.3090 + 0.9511i
   0.3090 - 0.9511i
   1.0000 + 0.0000i

直交座標で 1 の複素根をプロットします。

plot(z,"o")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

極座標での複素数のプロット

polarplot を使用して、極座標で 1 の 5 乗根をプロットします。angle 関数を使用して、複素根の位相角を返します。また、abs 関数を使用して、複素根の絶対値 (半径) を返します。

polarplot(angle(z),abs(z),"o")

polarplot(angle(z),abs(z),LineSpec) の代わりに polarplot(z,LineSpec) を使用して、極座標で複素数の配列をプロットすることもできます。この関数は、複素数の半径と位相角を自動的にプロットします。

複素平面でのパラメトリック曲線のプロット

次の形式のパラメトリック曲線を定義します。

$$z=f(t)=t\exp (it)$$

パラメーター $$t$$ は区間 $$[0,4\pi ]$$ 内です。

この区間内に等間隔に配置された 200 個の点から成るベクトル t を作成して、$$t$$ をパラメーター化します。複素曲線上にある点を複素数ベクトル z として定義します。

t = linspace(0,4*pi,200);
z = t.*exp(1i*t);

直交座標で複素曲線をプロットします。

plot(z,"-")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

極座標で複素曲線をプロットします。

polarplot(z,"-")

正方行列の固有値のプロット

実数の $$n$$ 行 $$n$$ 列の正方行列には、実数または複素共役対として生じる $$n$$ 個の固有値 (代数的多重度を込めて数える) があります。

たとえば、標準正規分布からサンプリングされたランダム要素をもつ 20 行 20 列の実数行列を考えます。eig を使用して固有値を計算します。

rng("default")
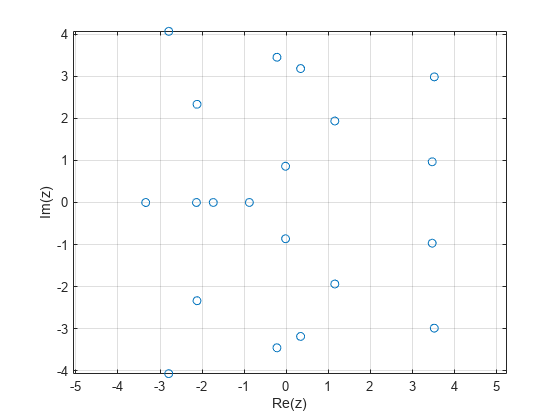
z = eig(randn(20));

20 個の固有値すべての虚数部と実数部をプロットします。実数軸上にない各固有値 $$z_k=x_k+y_{k}i$$ に対して、その固有値の複素共役対 $$z_k^{*}=x_k-y_{k}i$$ が存在することに注意してください。

plot(z,"o")
axis equal
grid on
xlabel("Re(z)")
ylabel("Im(z)")

複数の複素数データ セットのプロット

2 つの複素数データ セットの虚数部と実数部をプロットします。plot に複数の複素数入力引数を渡すと (plot(z1,z2) など)、plot 関数は虚数部を無視し、入力の実数部のみをプロットします。複数の複素数入力に対して実数部と虚数部をプロットするには、実数部と虚数部を plot に明示的に渡す必要があります。

たとえば、2 つの複素数ベクトル z1 と z2 を作成します。

x = -2:0.25:2;
z1 = x.^exp(-x.^2);
z2 = 2*x.^exp(-x.^2);

real 関数と imag 関数を使用して、各ベクトルの実数部と虚数部を求めます。

re_z1 = real(z1);
im_z1 = imag(z1);
re_z2 = real(z2);
im_z2 = imag(z2);

複素数データをプロットします。

plot(re_z1,im_z1,"*",re_z2,im_z2,"o")
axis equal
grid on
legend("z1","z2")
xlabel("Re(z)")
ylabel("Im(z)")

参考

plot | real | imag | polarplot | abs | angle