モデル検証用の周波数応答プロット

線形モデルの周波数応答プロットにより、ピーク応答の周波数と安定余裕を含む、モデルダイナミクスの特性について詳しい情報が得られます。周波数応答プロットを使用すると、線形パラメトリックモデルが、どれくらい良好にダイナミクスを捉えているかの検証に役立ちます。System Identification Toolbox™ には、プロットオプションがいくつか用意されています。

周波数応答とは

"周波数応答" プロットは、伝達関数の複素数値を周波数の関数として示します。

線形動的システムの場合、伝達関数 G は実質的に、出力 y に対して線形システムの入力 u を取る演算子です。

$y = G u$

連続時間システムの場合、伝達関数は入力 U(s) と出力 Y(s) のラプラス変換に関連します。

$Y (s) = G (s) U (s)$

この場合、周波数関数 G(iω) は虚軸 s=iω で評価された伝達関数です。

時間間隔 T でサンプリングされた離散時間システムの場合、伝達関数は入力 U(z) と出力 Y(z) の Z 変換に関連します。

$Y (z) = G (z) U (z)$

この場合、周波数関数 $G e^{i ω T}$ は単位円で評価された伝達関数 G(z) です。周波数関数 $G e^{i ω T}$ の引数はサンプル時間 T でスケーリングされ、サンプリング周波数 $\frac{2 π}{T}$ で周波数関数を周期的にします。

モデル検証のための周波数応答の使用

線形動的モデルの周波数応答は、正弦波入力に対してどのようにモデルが反応するのかを記述します。入力 u(t) が特定の周波数の正弦波である場合、出力 y(t) も同じ周波数の正弦波です。ただし、応答の振幅は入力信号の振幅とは異なり、応答の位相は入力信号に対してシフトされます。

周波数応答プロットにより、周波数に依存するゲイン、共振、位相シフトなど、線形システムのダイナミクスについて詳しい情報が得られます。周波数応答プロットには、コントローラー要件と達成可能な帯域幅に関する情報も含まれています。

周波数応答プロットは、線形 ARX モデルや状態空間モデル、周波数応答モデルなどの線形パラメトリックモデルが、どれくらい良好にダイナミクスを捉えるのかを検証する場合にも役立ちます。たとえば、スペクトル解析 (ノンパラメトリックモデル) を使用して推定データから周波数応答を推定し、パラメトリックモデルの周波数応答の上にスペクトル解析結果をプロットできます。ノンパラメトリックモデルとパラメトリックモデルはさまざまなアルゴリズムを使用して派生するため、これらのモデル間の一致はパラメトリックモデルの結果における信頼度を向上させます。モデルの比較にスペクトル解析を使用する例については、Identify Time Series Models at the Command Lineを参照してください。

周波数応答プロットのオプション

System Identification Toolbox では、周波数応答プロットのオプションが 3 つ用意されています。

線形入出力モデルおよび周波数応答データモデル
- bode — 対数の周波数スケールで周波数応答の振幅と位相をプロットします。ボード線図は 2 つのプロットで構成されます。上部のプロットには、伝達関数 "G" が正弦波入力の振幅を拡大する振幅 $| G |$ が示されます。下部のプロットには、伝達関数が入力をシフトする位相 $φ = \arg G$ が示されます。システムへの入力は正弦波であり、出力も同じ周波数をもつ正弦波です。
  System Identification アプリの場合、[Model Views] の [Frequency resp] オプションを使用して、ボード線図を作成します。
- nyquist — 伝達関数の実数部に対する虚数部をプロットします。モデルが伝達関数以外の形式の場合、nyquist は最初にモデルを伝達関数に変換します。ナイキスト線図が得られるのは、コマンドラインのみです。
次の時系列 (入力なし) モデルを含むすべての線形モデル:
- spectrum — 時系列モデルの出力パワースペクトルまたは線形入出力モデルの外乱スペクトルをプロットします。外乱スペクトルは "ノイズスペクトル" とも呼ばれます。このプロットはモデル応答のボード線図と同じですが、ノイズモデルの出力パワースペクトルを代わりに示します。詳細については、Noise Spectrum Plotsを参照してください。
  System Identification アプリの場合、[Model Views] の [Noise spectrum] オプションを使用して、パワースペクトルプロットを作成します。

この図は 3 種類の周波数プロットを示しています。すべてコマンドラインで作成されています。

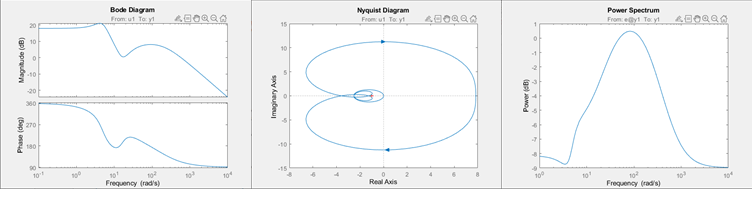
Bode plot, Nyquist plot, and spectrum plot, side by side

プロットの外観をカスタマイズするか、プログラムで信頼領域をオンにする場合は、bodeplot、nyquistplot、または spectrumplot を使用します。

各コマンドの例および詳細については、該当するリファレンスページを参照してください。System Identification アプリで周波数応答を取得する方法の詳細については、Identify Linear Models Using System Identification App、Plot Bode Plots Using the System Identification App、およびPlot the Noise Spectrum Using the System Identification Appを参照してください。

信頼区間の表示

周波数応答曲線に加えて、信頼区間を表現する領域をプロットに表示できます。

コマンドラインで生成したプロットに信頼区間を表示するには、プロットを右クリックして [特性]、[信頼領域] を選択します。既定では、このプロットには 1 標準偏差、すなわち 95% の領域が表示されます。この区間を変更するには、プロットを右クリックし、[プロパティ] を選択します。次に、プロパティエディターの [オプション] タブで、[表示する標準偏差の数] を変更します。
アプリで信頼区間を表示するには [Options]、[Show 97% confidence intervals] を選択するか、別のサイズ区間の場合は、[Options]、[Set Confidence level] から選択します。

"信頼区間" はシステムの実際の応答である特定の確率をもつ応答値の範囲に対応します。ツールボックスはモデルパラメーターの推定された不確かさを使用して信頼区間を計算し、推定にガウス分布があると仮定します。

たとえば、95% 信頼区間の場合、ノミナル曲線周辺の領域は、真のシステム応答が含まれる確率が 95% の範囲を表します。信頼区間を確率 (0 と 1 の間) またはガウス分布の標準偏差の数として指定できます。たとえば、0.99 (99%) の確率は 2.58 の標準偏差に対応します。

次の図は、コマンドラインで生成されたボード線図の信頼領域の例を示しています。

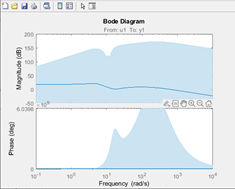
Bode plot that displays the confidence region within a blue shaded area.

参考