周波数領域同定: 周波数領域データを使用したモデルの推定
この例では、周波数領域データを使用してモデルを推定する方法を説明します。周波数領域データを使用したモデルの推定と検証は、時間領域データの場合と同じように機能します。これにより、時間領域、周波数領域およびスペクトル (FRF) データを使用してモデルを推定および解析するときに大きな柔軟性を得られます。両方の領域のデータを使用してモデルを同時に推定し、これらのモデルを比較および結合することができます。時間領域データを使用して推定したモデルは、スペクトル データを使用して検証できます (この反対も当てはまります)。
周波数領域データは、非線形モデルの推定や検証には使用できません。
はじめに
周波数領域実験データは、多くのアプリケーションで一般的です。データは、周波数アナライザーを使用して、周波数応答データ (周波数関数: FRF) としてプロセスから収集できます。また、たとえば、周期または帯域制限データを処理する場合など、入力および出力のフーリエ変換 (時間領域データの FFT) を使用することがより実用的です (帯域制限連続時間信号には、ナイキスト周波数を超える周波数要素はありません)。System Identification Toolbox™ では、周波数領域 I/O データが時間領域データと同じように表示されます (すなわち、iddata オブジェクトを使用)。オブジェクトの "Domain" プロパティは、"Frequency" に設定しなければなりません。周波数応答データは、周波数の関数で複素数ベクトルまたは振幅/位相ベクトルとして表されます。ツールボックスの IDFRD オブジェクトは、FRF をカプセル化するために使用します。このような IDDATA または IDFRD オブジェクト (および Control System Toolbox の FRD オブジェクト) は、いずれの推定ルーチン (procest、tfest など) でもシームレスに使用できます。
周波数領域データの調査
それではまず、周波数領域データの一部を読み込んでみましょう。
load demofr
この MAT ファイルには、周波数 W での周波数応答データと、振幅応答 AMP および位相応答 PHA が含まれます。まず、データをよく見てください。
subplot(211), loglog(W,AMP),title('Amplitude Response') subplot(212), semilogx(W,PHA),title('Phase Response')

この実験データは、IDFRD オブジェクトに格納されます。振幅と位相を複素数値の応答に変換します。
zfr = AMP.*exp(1i*PHA*pi/180); Ts = 0.1; gfr = idfrd(zfr,W,Ts);
Ts は基になるデータのサンプル時間です。データが連続時間に対応する場合、たとえば、入力が帯域制限である場合、Ts = 0 を使用します。
メモ: Control System Toolbox™ がある場合、IDFRD オブジェクトの代わりに FRD オブジェクトを使用できます。IDFRD には、FRD オブジェクトでは利用できない不確かさの測定や外乱スペクトルなど、より多くの情報オプションがあります。
IDFRD オブジェクト gfr には、データが含まれ、さまざまな方法でプロットおよび解析できます。データを表示するには、plot または bode を使用できます。
clf
bode(gfr), legend('gfr')

周波数応答 (FRF) データを使用したモデルの推定
モデルを推定するには、gfr をデータセットとして、ツールボックスのすべてのコマンドで透過的に使用することができます。唯一の制約は、ノイズ モデルを構築できないことです。これはつまり、多項式モデルには OE (出力誤差モデル) のみが適用され、状態空間モデルの場合、K = 0 を固定する必要があることを意味します。
m1 = oe(gfr,[2 2 1]) % Discrete-time Output error (transfer function) model ms = ssest(gfr) % Continuous-time state-space model with default choice of order mproc = procest(gfr,'P2UDZ') % 2nd-order, continuous-time model with underdamped poles compare(gfr,m1,ms,mproc) L = findobj(gcf,'type','legend'); L.Location = 'southwest'; % move legend to non-overlapping location
m1 =
Discrete-time OE model: y(t) = [B(z)/F(z)]u(t) + e(t)
B(z) = 0.9986 z^-1 + 0.4968 z^-2
F(z) = 1 - 1.499 z^-1 + 0.6998 z^-2
Sample time: 0.1 seconds
Parameterization:
Polynomial orders: nb=2 nf=2 nk=1
Number of free coefficients: 4
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using OE on frequency response data "gfr".
Fit to estimation data: 88.04%
FPE: 0.2512, MSE: 0.2492
ms =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2
x1 -1.785 3.097
x2 -6.835 -1.785
B =
u1
x1 -4.15
x2 27.17
C =
x1 x2
y1 1.97 0.3947
D =
u1
y1 0
K =
y1
x1 0
x2 0
Parameterization:
FREE form (all coefficients in A, B, C free).
Feedthrough: none
Disturbance component: none
Number of free coefficients: 8
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on frequency response data "gfr".
Fit to estimation data: 88.04%
FPE: 0.2512, MSE: 0.2492
mproc =
Process model with transfer function:
1+Tz*s
G(s) = Kp * ---------------------- * exp(-Td*s)
1+2*Zeta*Tw*s+(Tw*s)^2
Kp = 7.4523
Tw = 0.20266
Zeta = 0.36165
Td = 0
Tz = 0.01407
Parameterization:
{'P2DUZ'}
Number of free coefficients: 5
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on frequency response data "gfr".
Fit to estimation data: 88.04%
FPE: 0.2517, MSE: 0.2492

前述のように、スペクトル データを使用すると、さまざまな種類の線形モデルを連続および離散時間領域で推定できます。これらのモデルは、時間領域データを使用して検証できます。たとえば、時間領域 I/O データセット ztime は同じシステムから収集され、m1、ms および mproc の検証に使用できます。
compare(ztime,m1,ms,mproc) %validation in a different domain

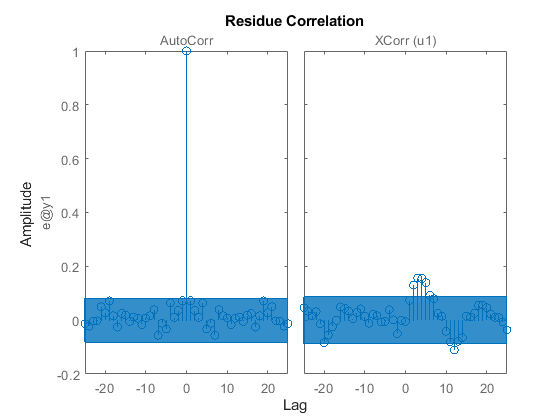
また、検証データ ztime を使用してモデルの質を確認するため、残差も調査できます。ご覧のように、残差はほぼホワイトとなります。
resid(ztime,mproc) % Residuals plot
SPAFDR を使用したデータの圧縮
周波数応答データを使用する重要な理由として、ほとんど損失なく、情報を圧縮できることがあげられます。コマンド SPAFDR は、限られた周波数で円滑化された応答データを算出できます (例: 対数空間)。gfr データが 100 の対数空間周波数値に圧縮された例を示します。同じように、元の時間領域データを圧縮することもできます。
sgfr = spafdr(gfr) % spectral estimation with frequency-dependent resolution sz = spafdr(ztime); % spectral estimation using time-domain data clf bode(gfr,sgfr,sz) axis([pi/100 10*pi, -272 105]) legend('gfr (raw data)','sgfr','sz','location','southwest')
sgfr = IDFRD model. Contains Frequency Response Data for 1 output(s) and 1 input(s), and the spectra for disturbances at the outputs. Response data and disturbance spectra are available at 100 frequency points, ranging from 0.03142 rad/s to 31.42 rad/s. Sample time: 0.1 seconds Output channels: 'y1' Input channels: 'u1' Status: Estimated using SPAFDR on frequency response data "gfr".
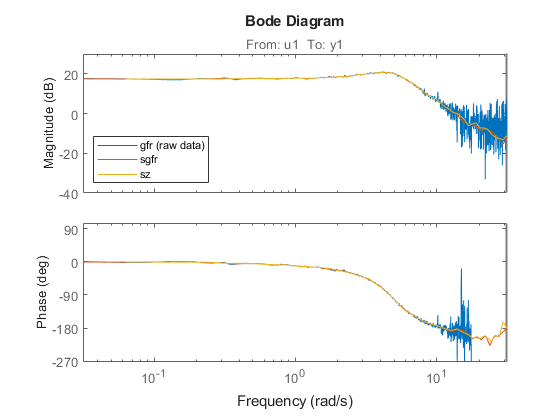
このボード線図は、円滑化されたデータの情報が正しく処理されていることを示します。100 ポイントを含むこれらのデータは、モデルの推定に正しく使用できます。以下に例を示します。
msm = oe(sgfr,[2 2 1]);
compare(ztime,msm,m1) % msm has the same accuracy as M1 (based on 1000 points)

周波数領域 I/O データを使用した推定
測定値は、入力および出力のフーリエ変換として取得できる場合があります。システムからのこのような周波数領域データは、信号 Y および U として取得されます。loglog プロットでは、似たようなデータに見えます。
Wfd = (0:500)'*10*pi/500; subplot(211),loglog(Wfd,abs(Y)),title('The amplitude of the output') subplot(212),loglog(Wfd,abs(U)),title('The amplitude of the input')

周波数応答データは基本的に、Y と U の割合となります。周波数領域データを IDDATA オブジェクトとして収集するには、以下を実行します。
ZFD = iddata(Y, U, 'Ts', 0.1, 'Frequency', Wfd)
ZFD =
Frequency domain data set with responses at 501 frequencies.
Frequency range: 0 to 31.416 rad/seconds
Sample time: 0.1 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
ここでも、時間領域データおよび周波数応答データと同じように、周波数領域応答データセット ZFD をすべての推定ルーチンのデータとして使用できます。
mf = ssest(ZFD) % SSEST picks best order in 1:10 range when called this way mfr = ssregest(ZFD) % an alternative regularized reduction based state-space estimator clf compare(ztime,mf,mfr,m1)
mf =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2
x1 -1.78 3.095
x2 -6.812 -1.78
B =
u1
x1 1.32
x2 28.61
C =
x1 x2
y1 2 6.468e-08
D =
u1
y1 0
K =
y1
x1 0
x2 0
Parameterization:
FREE form (all coefficients in A, B, C free).
Feedthrough: none
Disturbance component: none
Number of free coefficients: 8
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on frequency domain data "ZFD".
Fit to estimation data: 97.21%
FPE: 0.04288, MSE: 0.04186
mfr =
Discrete-time identified state-space model:
x(t+Ts) = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2 x3 x4 x5 x6
x1 0.701 -0.05307 -0.4345 -0.006642 -0.08085 -0.1158
x2 -0.4539 -0.09623 -0.3629 0.2113 -0.2219 0.3536
x3 0.1719 -0.3996 0.4385 -0.01558 0.1768 0.2467
x4 -0.1821 0.3465 0.3292 -0.1357 -0.2578 0.2483
x5 -0.09939 -0.338 0.1236 -0.2537 -0.387 0.05591
x6 -0.06004 0.226 0.04117 -0.6891 -0.0873 0.2818
x7 -0.1056 0.1859 0.04223 -0.629 0.1968 -0.7077
x8 0.05337 0.1948 0.06355 -0.09052 0.4216 0.3997
x9 -0.01696 -0.05961 -0.04891 -0.01251 -0.03521 -0.3876
x10 -0.01727 -0.1232 -0.03586 0.1187 -0.1738 -0.05051
x7 x8 x9 x10
x1 -0.3087 0.007547 0.02011 -0.1469
x2 -0.01728 -0.04967 0.1144 0.03883
x3 0.07107 -0.2977 -0.129 -0.06179
x4 0.08461 0.03541 -0.06711 -0.1759
x5 -0.5324 0.1778 -0.1114 -2.119e-05
x6 0.155 -0.5047 0.285 0.3976
x7 -0.2406 0.5628 -0.09159 -0.4845
x8 -0.5674 -0.3337 0.105 0.1995
x9 -0.2024 -0.4718 -0.01861 -0.5838
x10 0.01243 0.2968 0.6808 -0.7726
B =
u1
x1 -0.09482
x2 0.7665
x3 -1.036
x4 0.162
x5 -0.2926
x6 0.0805
x7 -0.1277
x8 -0.02441
x9 0.0288
x10 0.03776
C =
x1 x2 x3 x4 x5 x6 x7
y1 1.956 -0.4539 -1.805 -1.356 0.3662 1.691 0.8489
x8 x9 x10
y1 0.148 -0.5203 -0.4013
D =
u1
y1 0
K =
y1
x1 0.1063
x2 -0.007395
x3 0.0426
x4 0.004966
x5 -0.01505
x6 -0.005483
x7 -0.0004218
x8 -0.001044
x9 0.003066
x10 0.002273
Sample time: 0.1 seconds
Parameterization:
FREE form (all coefficients in A, B, C free).
Feedthrough: none
Disturbance component: estimate
Number of free coefficients: 130
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSREGEST on frequency domain data "ZFD".
Fit to estimation data: 76.61% (prediction focus)
FPE: 3.448, MSE: 2.938
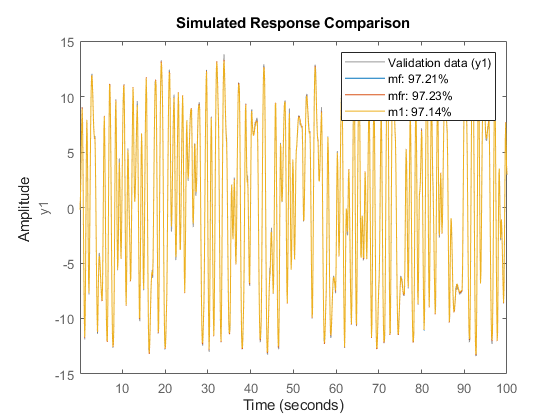
データ表現の変換 (時間 - 周波数)
時間および周波数領域入力/出力データセットは、FFT および IFFT を使用して、いずれかの領域に変換できます。以下のコマンドは、IDDATA オブジェクトに対応します。
dataf = fft(ztime) datat = ifft(dataf)
dataf =
Frequency domain data set with responses at 501 frequencies.
Frequency range: 0 to 31.416 rad/seconds
Sample time: 0.1 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
datat =
Time domain data set with 1000 samples.
Sample time: 0.1 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1
時間および周波数領域入力/出力データセットは、SPAFDR、SPA および ETFE を使用して、周波数応答データに変換できます。
g1 = spafdr(ztime) g2 = spafdr(ZFD); clf; bode(g1,g2)
g1 = IDFRD model. Contains Frequency Response Data for 1 output(s) and 1 input(s), and the spectra for disturbances at the outputs. Response data and disturbance spectra are available at 100 frequency points, ranging from 0.06283 rad/s to 31.42 rad/s. Sample time: 0.1 seconds Output channels: 'y1' Input channels: 'u1' Status: Estimated using SPAFDR on time domain data "ztime".
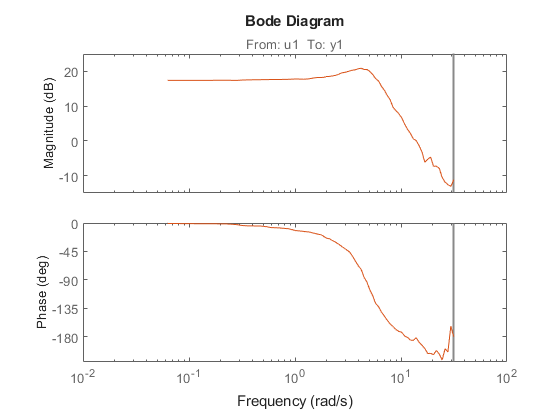
周波数応答データは、SPAFDR および SPA を使用して、より円滑なデータ (分解能とデータが少ない) に変換することもできます。
g3 = spafdr(gfr);
周波数応答データは、コマンド IDDATA を使用して、周波数領域入力/出力信号に変換できます。
gfd = iddata(g3) plot(gfd)
gfd =
Frequency domain data set with responses at 100 frequencies.
Frequency range: 0.031416 to 31.416 rad/seconds
Sample time: 0.1 seconds
Outputs Unit (if specified)
y1
Inputs Unit (if specified)
u1

連続時間周波数領域データを使用した連続時間モデルの推定
時間領域データは、離散時間サンプル データとしてのみ格納し、処理できます。周波数領域データは、連続時間データを正しく表現できるという利点があります。たとえば、クイック サンプル データであるため、あるいは入力にナイキスト周波数以上の周波数要素がないため、連続時間信号にナイキスト周波数以上の周波数情報がないと想定し、またデータが定常状態の実験から収集されたものと想定します。ここで、データの離散フーリエ変換 (DFT) は、選択した周波数で、連続時間信号のフーリエ変換でもあります。したがって、これらのデータを使用して、連続時間モデルに直接適合できます。
これは、以下の例で示すことができます。
連続時間システムを評価します。
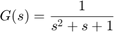
m0 = idpoly(1,1,1,1,[1 1 1],'ts',0)
m0 =
Continuous-time OE model: y(t) = [B(s)/F(s)]u(t) + e(t)
B(s) = 1
F(s) = s^2 + s + 1
Parameterization:
Polynomial orders: nb=1 nf=2 nk=0
Number of free coefficients: 3
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Created by direct construction or transformation. Not estimated.
周期的入力を使用して、このシステムの定常状態のシミュレーションから得られるデータを読み込みます。収集したデータは周波数領域に変換され、CTFDData.mat ファイルに保存されています。
load CTFDData.mat dataf % load continuous-time frequency-domain data.
このデータを見てみましょう。
plot(dataf)
set(gca,'XLim',[0.1 10])

dataf を推定に使用すると、既定の設定で連続時間モデルが作成されます。状態空間:
m4 = ssest(dataf,2); % Second order continuous-time model
nb = 2 の分子係数と nf = 2 の推定分母係数をもつ多項式モデルの場合、以下を使用します。
nb = 2; nf = 2; m5 = oe(dataf,[nb nf])
m5 =
Continuous-time OE model: y(t) = [B(s)/F(s)]u(t) + e(t)
B(s) = -0.01814 s + 1.008
F(s) = s^2 + 1.001 s + 0.9967
Parameterization:
Polynomial orders: nb=2 nf=2 nk=0
Number of free coefficients: 4
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using OE on frequency domain data "dataf".
Fit to estimation data: 70.15%
FPE: 0.00491, MSE: 0.00468
ステップ応答を、真のシステム m0 およびモデル m4 と m5 の不確かさと比較します。信頼区間はプロットにパッチで示されます。
clf h = stepplot(m0,m4,m5); showConfidence(h,1) legend('show','location','southeast')
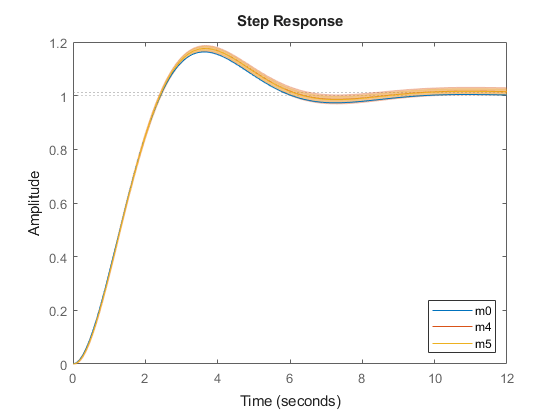
この事例では必要ありませんが、連続時間データを使用して推定を行なう場合、通常は適合の範囲を制限周波数帯域 (データをローパス フィルターで処理する) に的を絞ることをお勧めします。システムの帯域幅は約 3 rad/sで、最大 6.2 rad/s まで正弦波で励起されています。適合において的を絞る適切な周波数範囲は、[0 7] rad/s となります。
m6 = ssest(dataf,2,ssestOptions('WeightingFilter',[0 7])) % state space model
m6 =
Continuous-time identified state-space model:
dx/dt = A x(t) + B u(t) + K e(t)
y(t) = C x(t) + D u(t) + e(t)
A =
x1 x2
x1 -0.5011 1.001
x2 -0.7446 -0.5011
B =
u1
x1 -0.01706
x2 1.016
C =
x1 x2
y1 1.001 -0.0005347
D =
u1
y1 0
K =
y1
x1 0
x2 0
Parameterization:
FREE form (all coefficients in A, B, C free).
Feedthrough: none
Disturbance component: none
Number of free coefficients: 8
Use "idssdata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using SSEST on frequency domain data "dataf".
Fit to estimation data: 87.03% (data prefiltered)
FPE: 0.004832, MSE: 0.003631
m7 = oe(dataf,[1 2],oeOptions('WeightingFilter',[0 7])) % polynomial model of Output Error structure
m7 =
Continuous-time OE model: y(t) = [B(s)/F(s)]u(t) + e(t)
B(s) = 0.9861
F(s) = s^2 + 0.9498 s + 0.9704
Parameterization:
Polynomial orders: nb=1 nf=2 nk=0
Number of free coefficients: 3
Use "polydata", "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using OE on frequency domain data "dataf".
Fit to estimation data: 86.81% (data prefiltered)
FPE: 0.004902, MSE: 0.003752
opt = procestOptions('SearchMethod','lsqnonlin',... 'WeightingFilter',[0 7]); % Requires Optimization Toolbox(TM) m8 = procest(dataf,'P2UZ',opt) % process model with underdamped poles
m8 =
Process model with transfer function:
1+Tz*s
G(s) = Kp * ----------------------
1+2*Zeta*Tw*s+(Tw*s)^2
Kp = 1.0124
Tw = 1.0019
Zeta = 0.5021
Tz = -0.017474
Parameterization:
{'P2UZ'}
Number of free coefficients: 4
Use "getpvec", "getcov" for parameters and their uncertainties.
Status:
Estimated using PROCEST on frequency domain data "dataf".
Fit to estimation data: 87.03% (data prefiltered)
FPE: 0.004832, MSE: 0.003631
opt = tfestOptions('SearchMethod','lsqnonlin',... 'WeightingFilter',[0 7]); % Requires Optimization Toolbox m9 = tfest(dataf,2,opt) % transfer function with 2 poles
m9 = From input "u1" to output "y1": -0.01662 s + 1.007 ------------------ s^2 + s + 0.995 Continuous-time identified transfer function. Parameterization: Number of poles: 2 Number of zeros: 1 Number of free coefficients: 4 Use "tfdata", "getpvec", "getcov" for parameters and their uncertainties. Status: Estimated using TFEST on frequency domain data "dataf". Fit to estimation data: 87.03% (data prefiltered) FPE: 0.00491, MSE: 0.003629
h = stepplot(m0,m6,m7,m8,m9);
showConfidence(h,1)
legend('show')

まとめ
時間、周波数およびスペクトル データをシームレスに使用して、連続および離散時間領域で各種の線形モデルを推定する方法を説明してきました。モデルは、推定したときと異なる領域で検証および比較できます。データ形式 (時間、周波数、およびスペクトル) は、fft、ifft、spafdr、spa などのメソッドを使用して相互互換が可能です。さらに、tfest、ssest、procest の各推定ルーチンを使用して、直接連続時間推定を実行できます。推定および解析にいずれかの領域のデータをシームレスで使用できることが、System Identification Toolbox の重要な機能です。