Tuning Fuzzy Inference Systems
Designing a complex fuzzy inference system (FIS) with a large number of inputs and membership functions (MFs) is a challenging problem due to the large number of MF parameters and rules. To design such a FIS, you can use a data-driven approach to learn rules and tune FIS parameters. To tune a fuzzy system, you can use:
Fuzzy Logic Designer — Interactively tune FIS rules and parameters (since R2023a)
tunefis— Programmatically tune FIS rules and parameters
Using Fuzzy Logic Toolbox™ software, u can tune the following types of fuzzy systems.
Type-1 FIS — For examples, see Tune Mamdani Fuzzy Inference System and Tune Fuzzy Inference System Using Fuzzy Logic Designer.
Type-2 FIS — For an example, see Predict Chaotic Time Series Using Type-2 FIS.
FIS tree — For examples, see Tune FIS Tree at the Command Line and Tune FIS Tree Using Fuzzy Logic Designer.
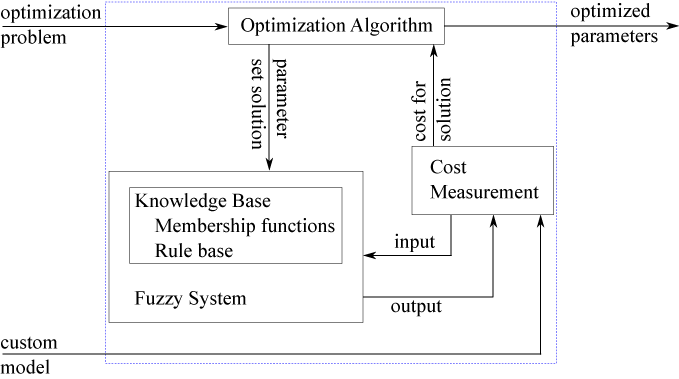
During tuning, the optimization algorithm generates candidate FIS parameter sets. The fuzzy system is updated with each parameter set and then evaluated using the a cost function.
If you have input/output training data, the cost function for each solution is computed based on the difference between the output of the fuzzy system and the expected output values from the training data. For examples that use this approach, see Tune Fuzzy Inference System Using Fuzzy Logic Designer and Tune Mamdani Fuzzy Inference System.

If you do not have input/output training data, you can specify a custom model and cost function for evaluating candidate FIS parameter sets. The cost measurement function sends an input to the fuzzy system and receives the evaluated output. The cost is based on the difference between the evaluated output and the output expected by the model. For more information and an example that uses this approach, see Tune Fuzzy Robot Obstacle Avoidance System Using Custom Cost Function.
Tuning Methods
The following table shows the tuning methods supported by Fuzzy Logic
Designer and tunefis function.
| Method | Description | More Information |
|---|---|---|
| Genetic algorithm | Population-based global optimization method that searches randomly by mutation and crossover among population members | What Is the Genetic Algorithm? (Global Optimization Toolbox) |
| Particle swarm optimization | Population-based global optimization method in which population members step throughout a search region | What Is Particle Swarm Optimization? (Global Optimization Toolbox) |
| Pattern search | Direct-search local optimization method that searches a set of points near the current point to find a new optimum | What Is Direct Search? (Global Optimization Toolbox) |
| Simulated annealing | A local optimization method that simulates a heating and cooling process to that finds a new optimal point near the current point | What Is Simulated Annealing? (Global Optimization Toolbox) |
| Adaptive neuro-fuzzy inference | Back-propagation algorithm that tunes membership function
parameters. Alternatively, you can use the anfis function. | Neuro-Adaptive Learning and ANFIS |
The first four tuning methods require Global Optimization Toolbox software.
Global optimization methods, such as genetic algorithms and particle swarm optimization, perform better for large parameter tuning ranges. These algorithms are useful for both the rule-learning and parameter-tuning stages of FIS optimization.
On the other hand, local search methods, such as pattern search and simulated annealing, perform better for small parameter ranges. If you generate a FIS from training data or a rule base is already added to a FIS, then these algorithms can produce faster convergence compared to global optimization methods.
Prevent Overfitting of Tuned System
Data overfitting is a common problem in FIS parameter optimization. When overfitting occurs, the tuned FIS produces optimized results for the training data set but performs poorly for a test data set. To overcome the data overfitting problem, a tuning process can stop early based on an unbiased evaluation of the model using a separate validation dataset.
You can prevent overfitting using k-fold cross validation. For more information and a command-line example, see Optimize FIS Parameters with K-Fold Cross-Validation. You can also configure k-fold cross validation when setting the tuning options in Fuzzy Logic Designer. For more information, see Configure Tuning Options in Fuzzy Logic Designer.
The ANFIS tuning method does not support k-fold cross validation. Instead, you must specify separate validation data. For more information, see Neuro-Adaptive Learning and ANFIS.
Improve Tuning Results
To improve the performance of your tuned fuzzy systems, consider the following guidelines.
Use multiple phases in your tuning process. For example, first learn the rules of a fuzzy system, and then tune input/output MF parameters using the learned rule base.
Increase the number of iterations in both the rule-learning and parameter-tuning phases. Doing so increases the duration of the optimization process and can also increase validation error due to overtuned system parameters with the training data. To avoid overfitting, train your system using k-fold cross validation.
Change the clustering technique when you create a FIS from data. Depending on the clustering technique, the generated rules can differ in their representation of the training data, which can affect the tuning performance.
Change FIS properties. Try changing properties such as the type of FIS, number of inputs, number of input/output MFs, MF types, and number of rules. A Sugeno system has fewer output MF parameters (assuming constant MFs) and faster defuzzification. Therefore, for fuzzy systems with a large number of inputs, a Sugeno FIS generally converges faster than a Mamdani FIS. Small numbers of MFs and rules reduce the number of parameters to tune, producing a faster tuning process. Furthermore, a large number of rules might overfit the training data.
Modify tunable parameter settings for MFs and rules. For example, you can tune the support of a triangular MF without changing its peak location. Doing so reduces the number of tunable parameters and can produce a faster tuning process for specific applications. For rules, you can exclude zero MF indices, which reduces the overall number of rules during the learning phase.
To improve the tuning results for FIS trees, consider the following guidelines.
If you have the corresponding training data, you can separately tune the parameters of each FIS in a FIS tree. You can then tune all the fuzzy systems together to generalize the parameter values.
Change FIS tree properties, such as the number of fuzzy systems and the connections between the fuzzy systems.
Use different rankings and groupings of the inputs to a FIS tree. For more information about creating FIS trees, see Fuzzy Trees.
See Also
Apps
Functions
Topics
- Tune Fuzzy Inference System Using Fuzzy Logic Designer
- Tune FIS Tree Using Fuzzy Logic Designer
- Tune Fuzzy Inference System at the Command Line
- Tune FIS Tree at the Command Line
- Predict Chaotic Time Series Using Type-2 FIS
- Customize FIS Tuning Process