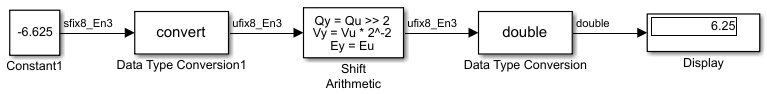算術演算の規則

固定小数点演算は、符号付きまたは符号なしのバイナリワードが処理される方法を指します。加算や減算のような固定小数点の算術関数の単純性が、費用効果の高いハードウェア実行を可能にします。

以下の節では、入力とパラメーターに算術演算を実行するときに Simulink^® ソフトウェアが従う規則について説明します。これらの規則は、必要とする演算に基づいて、加算と減算、乗算、除算、シフトの 4 つのグループに分類されます。これらのグループごとに、指定した演算を実行する規則を、例を挙げて説明します。

計算単位

多くの場合、プロセッサの中核となるアーキテクチャには、ALU (arithmetic logic units)、MAC (multiply and accumulate units)、シフターなどの複数の計算単位が含まれています。これらの計算単位はバイナリデータを直接処理し、さまざまな精度の算術計算をサポートしています。ALU は標準的な算術演算と論理演算のほかに除算も実行します。MAC は乗算、乗算/加算、および乗算/減算の演算を実行します。シフターは論理シフトと算術シフト、正規化、非正規化や、その他の演算を実行します。

加算と減算

加算は、プロセッサが実行する最も一般的な算術演算です。n ビットの 2 つの数を加算すると、左端の数字からの桁上げによって、n + 1 の非零数を使用した結果が出る可能性が常にあります。2 つの数値の 2 の補数加算については、次の 3 とおりの状況を考慮する必要があります。

両方の数値が正で、加算の結果に符号ビット 1 がある場合は、オーバーフローが発生します。そうでない場合は、正しい結果になります。
両方の数値が負で、結果の符号が 0 の場合は、オーバーフローが発生します。そうでない場合は、正しい結果になります。
数値が異なる符号の場合は、オーバーフローが発生し、常に正しい結果になります。

固定小数点 Simulink ブロックの総和処理

2 つの数値の総和を考えてみましょう。実際値が次の方程式に従うのが理想的です。

$V_{a} = \pm V_{b} \pm V_{c},$

ここで、V_b と V_c は入力値で、V_a は出力値です。総和が実際にどのように実行されるかを見るため、スケーリングの説明に従って 3 つの理想値を一般的な [傾きバイアス] エンコードスキームに置き換えます。

$V_{i} = F_{i} 2^{E_{i}} Q_{i} + B_{i} .$

加算の方程式は、整数格納、Q_a に結果の方程式の解を提供します。省略形表記を使用すると、その方程式は次のようになります。

$Q_{a} = \pm F_{s b} 2^{E_{b} - E_{a}} Q_{b} \pm F_{s c} 2^{E_{c} - E_{a}} Q_{c} + B_{n e t},$

ここで、F_sb と F_sc は調整後の小数部の傾きで、B_net は正味バイアスです。以下に、オフライン変換とオンライン変換、および演算について説明します。

オフライン変換. F_sb、F_sc、および B_net は最も近い整数への丸めと飽和を使用してオフラインで計算されます。さらに、出力データ型を使用して B_net が格納されます。

オンライン変換と演算. 残りの演算は、固定小数点プロセッサによってオンラインで実行され、入力データ型と出力データ型の傾きとバイアスに依存します。最悪の (最も非効率的な) 場合は、傾きとバイアスが不一致のときに発生します。最悪の場合の変換と演算は以下の手順で行われます。

Q_a の初期値は正味バイアス、B_net によって提供されます。
$Q_{a} = B_{n e t} .$
最初の入力整数値、Q_b が調整後の傾き、F_sb で乗算されます。
$Q_{R a w P r o d u c t} = F_{s b} Q_{b} .$
前の積は、傾きが 1 でバイアスがゼロの調整後のデータ型に変換されます。
$Q_{T e m p} = c o n v e r t (Q_{R a w P r o d u c t}) .$
この変換には、必要なビットシフト、丸め、オーバーフロー処理などが含まれます。
総和演算は次のように実行されます。
$Q_{a} = Q_{a} \pm Q_{T e m p} .$
この総和演算には必要なオーバーフロー処理が含まれます。
合計するすべての数値に手順 2 から 4 を繰り返します。

ビットシフト、丸め、およびオーバーフローの処理は、合計全体にではなく中間手順 (3 と 4) に適用されます。

詳細は、総和処理を参照してください。

シミュレーションの効率化と生成コード

入力信号と出力信号のスケーリングが一致する場合は、総和演算回数が最悪の (最も非効率な) 場合から減少します。たとえば、入力の小数部の傾きが出力と同じ場合は、手順 2 が 1 の乗算に減少するので排除できます。シミュレーションとコード生成の両方で総和処理の小さい手順が排除されます。傾きとバイアスの不一致をなくす一般的な方法は、入力信号と出力信号の両方に対する 2 進小数点のみのスケーリングの排他的な使用で、最も効率的なシミュレーションと生成コードになります。

乗算

n ビットの 2 進数に m ビットの 2 進数を掛けると、符号付きワードでも符号なしワードでも最大長が m + n ビットの積になります。ほとんどのプロセッサにはオーバーフロー状態がないと仮定して、n ビット掛ける n ビットの乗算を実行し、2n ビットの結果 (ダブルビット) を生成します。

固定小数点 Simulink ブロックの乗算プロセス

2 つの数値の乗算を考えてみましょう。実際値が次の方程式に従うのが理想的です。

$V_{a} = V_{b} V_{c} .$

ここで、V_b と V_c は入力値で、V_a は出力値です。乗算が実際にどのように実行されるかを見るため、スケーリングの説明に従って 3 つの理想値を一般的な [傾きバイアス] エンコードスキームに置き換えます。

$V_{i} = F_{i} 2^{E_{i}} Q_{i} + B_{i} .$

その結果、出力整数格納、Q_a の方程式の解は以下のようになります。

$\begin{matrix} Q_{a} = \frac{F_{b} F_{c}}{F_{a}} 2^{E_{b} + E_{c} - E_{a}} Q_{b} Q_{c} + \frac{F_{b} B_{c}}{F_{a}} 2^{E_{b} - E_{a}} Q_{b} \\ + \frac{F_{c} B_{b}}{F_{a}} 2^{E_{c} - E_{a}} Q_{c} + \frac{B_{b} B_{c} - B_{a}}{F_{a}} 2^{- E_{a}} . \end{matrix}$

非零バイアスを使用する乗算と不一致の小数部の傾き. 上の方程式の実装の最悪の場合は、入力信号と出力信号の傾きとバイアスが不一致のときに発生します。そのような場合は、高水準の乗算 (または除算) を実行するために複数の低水準の整数演算が必要になります。これら低水準の計算について行った実装の選択は、計算の効率性や、丸め誤差、オーバーフローに影響する場合があります。

Simulink ブロックでは、乗算や除算の実際の演算は常に、バイアスがゼロの固定小数点変数に実行されます。入力のバイアスが非零の場合は、演算の前に 2 進小数点のみのスケーリングのある表現に変換されます。結果が非零のバイアスになる場合は、演算はまず 2 進小数点のみのスケーリングのある一時変数を使用して実行されます。次に、結果が最終出力のデータ型とスケーリングに変換されます。

入力と出力の両方に非零のバイアスがある場合は、演算が次のように分割されます。

$\begin{array}{l} V_{1 T e m p} = V_{1}, \\ V_{2 T e m p} = V_{2}, \\ V_{3 T e m p} = V_{1 T e m p} V_{2 T e m p}, \\ V_{3} = V_{3 T e m p}, \end{array}$

ここで、

$\begin{array}{l} V_{1 T e m p} = 2^{E_{1 T e m p}} Q_{1 T e m p}, \\ V_{2 T e m p} = 2^{E_{2 T e m p}} Q_{2 T e m p}, \\ V_{3 T e m p} = 2^{E_{3 T e m p}} Q_{3 T e m p} . \end{array}$

これらの方程式は、一時変数に 2 進小数点のみのスケーリングがあることを示しますが、変数の符号属性、語長、固定小数点の指数の値などは示しません。Simulink ソフトウェアは次の目標を踏まえて、一時変数にこれらのプロパティを代入します。

オーバーフローなしに元の値を表す。
元の値のデータ型とスケーリングは実際値の最大と最小を定義します。

$V_{M a x} = F 2^{E} Q_{M a x I n t e g e r} + B,$

$V_{M i n} = F 2^{E} Q_{M i n I n t e g e r} + B .$
一時的な値のデータ型とスケーリングはオーバーフローなしにこの範囲を表現できなければなりません。桁落ちはあり得ますが、オーバーフローは許可してはなりません。
効率的な演算を導くデータ型を使用する。
この目標は、設計の運用展開に使用するターゲットに関連します。たとえば、32 ビットの long、16 ビットの int、および 8 ビットの short または char を提供する 16 ビットの固定小数点プロセッサに設計を実装するとします。このターゲットの場合、効率性の維持とは、32 ビットより多くを使用せず、精度を十分に維持できる場合は 8 ビットや 16 ビットの小さいサイズを使用するという意味です。
精度を維持する。
理想的には、元のデータ型とスケーリングで定義された値はすべて一時変数によって完全に表現されなければなりません。しかし、これには効率的とは言えないほどのビットが必要になることがあります。効率性を維持するためにビットが破棄された結果、精度が低下します。

たとえば、16 ビットのマイクロプロセッサをターゲットと仮定し、以下を考慮してください。

$V_{O r i g i n a l} = Q_{O r i g i n a l} + - 43.25,$

ここで、Q_Original は 8 ビットの符号なしデータ型です。このデータ型の場合、

$\begin{matrix} Q_{M a x I n t e g e r} = 225, \\ Q_{M i n I n t e g e r} = 0, \end{matrix}$

したがって

$\begin{matrix} V_{M a x} = 211.75, \\ V_{M i n} = - 43.25. \end{matrix}$

可能な最小値は負であるため、一時変数は符号付きの整数データ型でなければなりません。元の変数の傾きは 1 ですが、バイアスは 2 進小数点の後の 2 桁を使用して高精度で表現されます。最大精度を得るには、一時変数の固定小数点指数が -2 より小さくなければなりません。Simulink ソフトウェアではできるだけ小さい精度が選択されます。これは、オーバーフローの問題が発生しない限り、通常は最も効率的な方法です。スケーリングが 2^-2 の場合は、符号付き 16 ビットまたは符号付き 32 ビットを選ぶと、オーバーフローを回避できます。効率性を高めるため、Simulink ソフトウェアでは小さい方の 16 ビットが選択されます。元の変数が入力値であれば、一時変数を変換する方程式は次のとおりです。

$\begin{array}{l} \begin{matrix} uint8_T & Q_{O r i g i n a l}, \\ uint16_T & Q_{T e m p}, \end{matrix} \\ Q_{T e m p} = ((int16_T) Q_{O r i g i n a l} ≪ 2) - 173. \end{array}$

バイアスがゼロで小数部の傾きが不一致の乗算. バイアスがゼロで小数部の傾きが不一致の場合、実装は次のように減少します。

$Q_{a} = \frac{F_{b} F_{c}}{F_{a}} 2^{E_{b} + E_{c} - E_{a}} Q_{b} Q_{c} .$

オフライン変換

次の量は、

$F_{N e t} = \frac{F_{b} F_{c}}{F_{a}}$

最も近い整数への丸めと飽和を使用してオフラインで計算されます。F_Net は、次の形式の固定小数点データ型を使用して格納されます。

$2^{E_{N e t}} Q_{N e t},$

E_Net と Q_Net は、F_Net の表現を最適化するように自動選択されます。

オンライン変換と演算

整数値 Q_b と Q_c は次のように乗算されます。
$Q_{R a w P r o d u c t} = Q_{b} Q_{c} .$
積の最大精度を維持するために、Q_b と Q_c の 2 進小数点の和によって Q_RawProduct の 2 進小数点が提供されます。
前の積が次の出力データ型に変換されます。
$Q_{T e m p} = c o n v e r t (Q_{R a w P r o d u c t}) .$
この変換には、必要なビットシフト、丸め、オーバーフロー処理などが含まれます。変換については信号の変換で説明しています。
乗算
$Q_{2 R a w P r o d u c t} = Q_{T e m p} Q_{N e t}$
が実行されます。
前の積が次の出力データ型に変換されます。
$Q_{a} = c o n v e r t (Q_{2 R a w P r o d u c t}) .$
この変換には、必要なビットシフト、丸め、オーバーフロー処理などが含まれます。変換については信号の変換で説明しています。
乗算する各数値につき、手順 1 ～ 4 を繰り返します。

バイアスがゼロで小数部の傾きが一致する乗算. バイアスがゼロで小数部の傾きが一致する場合、実装は次のように減少します。

$Q_{a} = 2^{E_{b} + E_{c} - E_{a}} Q_{b} Q_{c} .$

オフライン変換

オフライン変換は実行されません。

オンライン変換と演算

整数値 Q_b と Q_c は次のように乗算されます。
$Q_{R a w P r o d u c t} = Q_{b} Q_{c} .$
積の最大精度を維持するために、Q_b と Q_c の 2 進小数点の和によって Q_RawProduct の 2 進小数点が提供されます。
前の積が次の出力データ型に変換されます。
$Q_{a} = c o n v e r t (Q_{R a w P r o d u c t}) .$
この変換には、必要なビットシフト、丸め、オーバーフロー処理などが含まれます。変換については信号の変換で説明しています。
乗算する各数値につき、手順 1 と 2 を繰り返します。

詳細は、乗算処理を参照してください。

除算

この節では、ゼロバイアスの数量の除算について説明します。

メモ

除算の計算の入力値に非ゼロバイアスがある場合、実行される演算は非零バイアスを使用する乗算と不一致の小数部の傾きで説明した乗算の演算とまったく同じです。

固定小数点 Simulink ブロックの除算プロセス

2 つの数値の除算を考えてみましょう。実際値が次の方程式に従うのが理想的です。

$V_{a} = V_{b} / V_{c},$

ここで、V_b と V_c は入力値で、V_a は出力値です。除算が実際にどのように実装されるかを見るため、スケーリングの説明に従って 3 つの理想値を一般的な [傾きバイアス] エンコードスキームに置き換えます。

$V_{i} = F_{i} 2^{E_{i}} Q_{i} + B_{i} .$

すべての信号について、傾き調整係数 1 でバイアスがゼロの場合、出力整数格納 Q_a の結果の方程式の解は、次の方程式で提供されます。

$Q_{a} = 2^{E_{b} - E_{c} - E_{a}} (Q_{b} / Q_{c}) .$

この方程式には整数の除算とビットシフトが関係しています。E_a > E_b–E_c の場合、ビットシフトは右方向で、実装は簡単です。一方、E_a < E_b–E_c の場合、ビットシフトは左方向で、実装は複雑になることがあります。基本的な問題は、出力の精度の方が整数の除算が与える精度より高いことです。最大精度を得るには、"有理数" 除算が必要です。C プログラミング言語は、固定小数点データ型にのみ整数除算へのアクセスを提供します。分子のサイズによっては、整数除算の前にシフトを実行して小数部のビットをいくつか取得できます。最悪の場合では、ソフトウェアで減算を繰り返さなければならない可能性があります。

一般に、値の除算は固定小数点組み込みシステムでは避けたい演算です。出力が整数除算よりも精度が高い除算 (すなわち、E_a < E_b–E_c) の使用はお勧めできません。

詳細は、除算処理を参照してください。

シフト

ほとんどのマイクロプロセッサとデジタル信号プロセッサは、正しく定義された "ビットシフト" (略して "シフト") 整数演算をサポートしています。たとえば、8 ビットの符号なしの整数 00110101 を考えてみましょう。次の表に、2 ビット左シフトと 2 ビット右シフトの結果を示します。

シフト演算	バイナリ値	10 進数
シフトなし (元の番号)	00110101	53
2 ビット左シフト	11010100	212
2 ビット右シフト	00001101	13

Simulink Shift Arithmetic ブロックを使用してシフトを実行できます。ビットシフト、2 進小数点シフトまたはその両方を実行するには、このブロックを使用します。

ビット右シフト

右方向へシフトする特殊なケースでは、符号情報を含んでいる可能性のある左端ビットの処理を考慮する必要があります。右方向へのシフトは「"論理" 右シフト」または「"算術" 右シフト」として分類できます。論理右シフトの場合は、ビットシフトごとに最下位ビットに 0 が組み込まれます。算術右シフトの場合は、ビットシフトごとに最下位ビットが再循環します。

Shift Arithmetic ブロックは算術右シフトを実行するので、右ビットシフトごとに最下位ビットを再循環します。たとえば、下のモデルに示すように、固定小数点数が 11001.011 (-6.625) の場合、2 進小数点不動のまま 2 桁右へビットシフトした結果は 11110.010 (-1.75) となります。

Shift Arithmetic ブロックを使用して符号付き数値に論理右シフトを実行するには、Data Type Conversion ブロックを使用して、この数を同じ長さとスケーリングの符号なし数値としてキャストします。このモデルは、符号付き固定小数点数 11001.001 (-6.625) が 00110.010 (6.25) になることを示しています。