hwcalbyfloor
Calibrate Hull-White tree using floors
Syntax
Description
[
calibrates the Alpha,Sigma,OptimOut] = hwcalbyfloor(RateSpec,MarketStrikeMarketMaturity,MarketVolatility)Alpha (mean reversion) and Sigma
(volatility) using floor market data and the Hull-White model using the entire floor
surface.
The Hull-White calibration functions (hwcalbyfloor and hwcalbycap) support three models: Black (default), Bachelier or Normal, and
Shifted Black. For more information, see the optional arguments for
Shift and Model.
[
estimates the Alpha,Sigma,OptimOut = hwcalbyfloor(RateSpec,MarketStrikeMarketMaturity,MarketVolatility,Strike,Settle,Maturity)Alpha (mean reversion) and Sigma
(volatility) using floor market data and the Hull-White model to price a floor at a
particular maturity/volatility using the additional optional input arguments for
Strike, Settle, and
Maturity.
Strike, Settle, and
Maturity arguments are specified to calibrate to a specific point
on the market volatility surface. If omitted, the calibration is performed across all the
market instruments
For an example of calibrating using the Hull-White model with
Strike, Settle, and Maturity
input arguments, see Calibrating Hull-White Model Using Market Data.
[
adds optional name-value pair arguments. Alpha,Sigma,OptimOut] = hwcalbyfloor(___,Name,Value)
Examples
This example shows how to use hwcalbyfloor input
arguments for MarketStrike, MarketMaturity, and
MarketVolatility to calibrate the HW model using the entire floor
volatility surface.
Floor market volatility data covering two strikes over 12 maturity dates.
Reset = 4; MarketStrike = [0.0590; 0.0790]; MarketMaturity = [datetime(2008,3,21) ; datetime(2008,6,21) ; datetime(2008,9,21) ; datetime(2008,12,21) ; ... datetime(2009,3,21) ; datetime(2009,6,21) ; datetime(2009,9,21) ; datetime(2009,12,21); datetime(2010,3,21) ; ... datetime(2010,6,21); datetime(2010,9,21) ; datetime(2010,12,21)]; MarketVolaltility = [0.1533 0.1731 0.1727 0.1752 0.1809 0.1800 0.1805 0.1802 ... 0.1735 0.1757 0.1755 0.1755; 0.1526 0.1730 0.1726 0.1747 0.1808 0.1792 0.1797 0.1794 ... 0.1733 0.1751 0.1750 0.1745];
Plot market volatility surface.
[AllMaturities,AllStrikes] = meshgrid(MarketMaturity,MarketStrike); figure; surf(AllMaturities,AllStrikes,MarketVolaltility) xlabel('Maturity') ylabel('Strike') zlabel('Volatility') title('Market Volatility Data')

Set interest rate term structure and create a RateSpec.
Settle = '21-Jan-2008'; Compounding = 4; Basis = 0; Rates= [0.0627; 0.0657; 0.0691; 0.0717; 0.0739; 0.0755; 0.0765; 0.0772; 0.0779; 0.0783; 0.0786; 0.0789]; EndDates = [datetime(2008,3,21) ; datetime(2008,6,21) ; datetime(2008,9,21) ; datetime(2008,12,21) ; ... datetime(2009,3,21) ; datetime(2009,6,21) ; datetime(2009,9,21) ; datetime(2009,12,21); datetime(2010,3,21) ; ... datetime(2010,6,21); datetime(2010,9,21) ; datetime(2010,12,21)]; RateSpec = intenvset('ValuationDate', Settle, 'StartDates', Settle, ... 'EndDates', EndDates,'Rates', Rates, 'Compounding', Compounding, ... 'Basis',Basis)
RateSpec =
FinObj: 'RateSpec'
Compounding: 4
Disc: [12x1 double]
Rates: [12x1 double]
EndTimes: [12x1 double]
StartTimes: [12x1 double]
EndDates: [12x1 double]
StartDates: 733428
ValuationDate: 733428
Basis: 0
EndMonthRule: 1Calibrate Hull-White model from market data.
o = optimoptions('lsqnonlin','TolFun',1e-5,'Display','off'); [Alpha, Sigma] = hwcalbyfloor(RateSpec, MarketStrike, MarketMaturity, ... MarketVolaltility, 'Reset', Reset,'Basis', Basis, 'OptimOptions', o)
Warning: LSQNONLIN did not converge to an optimal solution. It exited with exitflag = 3.
> In hwcalbycapfloor>optimizeOverCapSurface at 232
In hwcalbycapfloor at 79
In hwcalbyfloor at 81
Alpha =
0.0835
Sigma =
0.0145
Compare with Black prices.
BlkPrices = floorbyblk(RateSpec,AllStrikes(:), Settle, AllMaturities(:), ... MarketVolaltility(:),'Reset',Reset,'Basis',Basis)
BlkPrices =
0
0.2659
0.0010
0.5426
0.0021
0.6841
0.0042
0.7947
0.0081
0.8970
0.0128
0.9947
0.0217
1.1145
0.0340
1.2448
0.0402
1.3415
0.0610
1.4947
0.0827
1.6458
0.1071
1.7951
Setup Hull-White tree using calibrated parameters, alpha, and sigma.
VolDates = EndDates; VolCurve = Sigma*ones(numel(EndDates),1); AlphaDates = EndDates; AlphaCurve = Alpha*ones(numel(EndDates),1); HWVolSpec = hwvolspec(Settle, VolDates, VolCurve, AlphaDates, AlphaCurve); HWTimeSpec = hwtimespec(Settle, EndDates, Compounding); HWTree = hwtree(HWVolSpec, RateSpec, HWTimeSpec, 'Method', 'HW2000')
HWTree =
FinObj: 'HWFwdTree'
VolSpec: [1x1 struct]
TimeSpec: [1x1 struct]
RateSpec: [1x1 struct]
tObs: [0 0.6593 1.6612 2.6593 3.6612 4.6593 5.6612 6.6593 7.6612 8.6593 9.6612 10.6593]
dObs: [733428 733488 733580 733672 733763 733853 733945 734037 734128 734218 734310 734402]
CFlowT: {1x12 cell}
Probs: {1x11 cell}
Connect: {1x11 cell}
FwdTree: {1x12 cell}Compute Hull-White prices based on the calibrated tree.
HWPrices = floorbyhw(HWTree, AllStrikes(:), Settle, AllMaturities(:), Reset, Basis)
HWPrices =
0
0.2644
0.0067
0.5404
0.0101
0.6924
0.0169
0.7974
0.0236
0.8919
0.0320
0.9919
0.0460
1.1074
0.0649
1.2340
0.0829
1.3558
0.1096
1.4957
0.1406
1.6418
0.1724
1.7877Plot Black prices against the calibrated Hull-White tree prices.
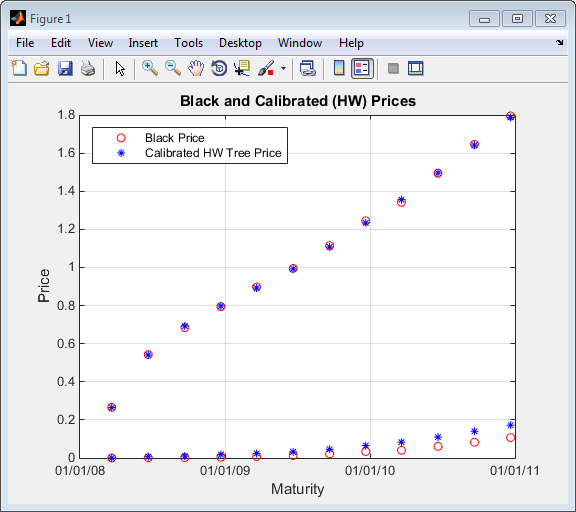
figure; plot(AllMaturities(:), BlkPrices, 'or', AllMaturities(:), HWPrices, '*b'); xtickformat; xlabel('Maturity'); ylabel('Price'); title('Black and Calibrated (HW) Prices'); legend('Black Price', 'Calibrated HW Tree Price','Location', 'NorthWest'); grid on
This example shows how to use hwcalbyfloor to calibrate market data with the Normal (Bachelier) model to price floorlets. Use the Normal (Bachelier) model to perform calibrations when working with negative interest rates, strikes, and normal implied volatilities.
Consider a floor with these parameters:
Settle = datetime(2016,12,30); Maturity = datetime(2019,12,30); Strike = -0.004075; Reset = 2; Principal = 100; Basis = 0;
The floorlets and market data for this example are defined as:
floorletDates = cfdates(Settle, Maturity, Reset, Basis); datestr(floorletDates')
ans = 6×11 char array
'30-Jun-2017'
'30-Dec-2017'
'30-Jun-2018'
'30-Dec-2018'
'30-Jun-2019'
'30-Dec-2019'
% Market data information MarketStrike = [-0.00595; 0]; MarketMat = [datetime(2017,6,30) ; datetime(2017,12,30) ; datetime(2018,6,30) ; datetime(2018,12,30) ; datetime(2019,6,30) ; datetime(2019,12,30)]; MarketVol = [0.184 0.2329 0.2398 0.2467 0.2906 0.3348; % First row in table corresponding to Strike 1 0.217 0.2707 0.2760 0.2814 0.3160 0.3508]; % Second row in table corresponding to Strike 2
Define the RateSpec using intenvset.
Rates= [-0.003210;-0.003020;-0.00182;-0.001343;-0.001075]; ValuationDate = datetime(2016,12,30); EndDates = [datetime(2017,6,30) ; datetime(2017,12,30) ; datetime(2018,6,30) ; datetime(2018,12,30) ; datetime(2019,12,30)]; Compounding = 2; Basis = 0; RateSpec = intenvset('ValuationDate', ValuationDate, ... 'StartDates', ValuationDate, 'EndDates', EndDates, ... 'Rates', Rates, 'Compounding', Compounding, 'Basis', Basis);
Use hwcalbyfloor to find values for the volatility parameters Alpha and Sigma using the Normal (Bachelier) model.
format short o=optimoptions('lsqnonlin','TolFun',100*eps); warning ('off','fininst:hwcalbycapfloor:NoConverge') [Alpha, Sigma, OptimOut] = hwcalbyfloor(RateSpec, MarketStrike, MarketMat,... MarketVol, Strike, Settle, Maturity, 'Reset', Reset, 'Principal', Principal,... 'Basis', Basis, 'OptimOptions', o, 'model', 'normal')
Local minimum possible. lsqnonlin stopped because the size of the current step is less than the value of the step size tolerance. <stopping criteria details>
Alpha = 1.0000e-06
Sigma = 0.3410
OptimOut = struct with fields:
resnorm: 1.9233e-04
residual: [5×1 double]
exitflag: 2
output: [1×1 struct]
lambda: [1×1 struct]
jacobian: [5×2 double]
The OptimOut.residual field of the OptimOut structure is the optimization residual. This value contains the difference between the Normal (Bachelier) floorlets and those calculated during the optimization. Use the OptimOut.residual value to calculate the percentual difference (error) compared to Normal (Bachelier) floorlet prices, and then decide whether the residual is acceptable. There is almost always some residual, so decide if it is acceptable to parameterize the market with a single value of Alpha and Sigma.
Price the floorlets using the market data and Normal (Bachelier) model to obtain the reference floorlet values. To determine the effectiveness of the optimization, calculate reference floorlet values using the Normal (Bachelier) formula and the market data. Note, you must first interpolate the market data to obtain the floorlets for calculation.
% MarketMatNum = datenum(MarketMat); [Mats, Strikes] = meshgrid(MarketMat, MarketStrike); MarketMat_T = yearfrac(Settle,Mats); Mats_T = yearfrac(Settle,Maturity); FlatVol = interp2(MarketMat_T, Strikes, MarketVol, Mats_T, Strike, 'spline'); % FlatVol = interp2(Mats, Strikes, MarketVol, datenum(Maturity), Strike, 'spline'); [FloorPrice, Floorlets] = floorbynormal(RateSpec, Strike, Settle, Maturity, FlatVol,... 'Reset', Reset, 'Basis', Basis, 'Principal', Principal); Floorlets = Floorlets(2:end)'
Floorlets = 5×1
4.7637
6.7180
8.1833
9.5825
10.6090
Compare the optimized values and Normal (Bachelier) values, and display the results graphically. After calculating the reference values for the floorlets, compare the values analytically and graphically to determine whether the calculated single values of Alpha and Sigma provide an adequate approximation.
OptimFloorlets = Floorlets+OptimOut.residual;
disp(' ');disp(' Bachelier Calibrated Floorlets');Bachelier Calibrated Floorlets
disp([Floorlets OptimFloorlets])
4.7637 4.7685
6.7180 6.7263
8.1833 8.1878
9.5825 9.5795
10.6090 10.6007
plot(MarketMat(2:end), Floorlets, 'or', MarketMat(2:end), OptimFloorlets, '*b'); xlabel('Floorlet Maturity'); ylabel('Floorlet Price'); ylim ([0 16]); title('Bachelier and Calibrated Floorlets'); h = legend('Bachelier Floorlets', 'Calibrated Floorlets'); set(h, 'color', [0.9 0.9 0.9]); set(h, 'Location', 'SouthEast'); set(gcf, 'NumberTitle', 'off') grid on

Input Arguments
Market floor strike, specified as a
NINST-by-1 vector.
Data Types: double
Market floor maturity dates, specified as a
NINST-by-1 vector using a datetime array, string
array, or date character vectors.
To support existing code, hwcalbyfloor also
accepts serial date numbers as inputs, but they are not recommended.
Market flat volatilities, specified as a
NSTRIKES-by-NMATS matrix of market flat
volatilities, where NSTRIKES is the number of caplet strikes from
MarketStrike and NMATS is the caplet
maturity dates from MarketMaturity.
Data Types: double
(Optional) Rate at which the floor is exercised, specified as a decimal scalar value.
Data Types: double
(Optional) Settlement date of the floor, specified as a scalar datetime, string, or data character vector.
To support existing code, hwcalbyfloor also
accepts serial date numbers as inputs, but they are not recommended.
(Optional) Maturity date of the floor, specified as scalar datetime, string, or data character vector.
To support existing code, hwcalbyfloor also
accepts serial date numbers as inputs, but they are not recommended.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: [Alpha,Sigma,OptimOut] =
hwcalbyfloor(RateSpec,MarketStrike,MarketMaturity,MarketVolaltility,'Reset',2,'Principal',100000,'Basis',3,'OptimOptions',o)
Frequency of payments per year, specified as the comma-separated pair consisting
of 'Reset' and a scalar numeric value.
Data Types: double
Notional principal amount, specified as the comma-separated pair consisting of
'Principal' and a scalar nonnegative integer.
Data Types: double
Day-count basis used when annualizing the input forward rate, specified as the
comma-separated pair consisting of 'Basis' and a scalar value.
Values are:
0 = actual/actual
1 = 30/360 (SIA)
2 = actual/360
3 = actual/365
4 = 30/360 (PSA)
5 = 30/360 (ISDA)
6 = 30/360 (European)
7 = actual/365 (Japanese)
8 = actual/actual (ICMA)
9 = actual/360 (ICMA)
10 = actual/365 (ICMA)
11 = 30/360E (ICMA)
12 = actual/365 (ISDA)
13 = BUS/252
For more information, see Basis.
Data Types: double
Lower bounds, specified as the comma-separated pair consisting of
'LB' and a 2-by-1 vector of
the lower bounds, defined as [LBSigma; LBAlpha], used in the search
algorithm function. For more information, see lsqnonlin.
Data Types: double
Upper bounds, specified as the comma-separated pair consisting of
'UB' and a 2-by-1 vector of
the upper bounds, defined as [UBSigma; LBAlpha], used in the search
algorithm function. For more information, see lsqnonlin.
Data Types: double
Initial values, specified as the comma-separated pair consisting of
'XO' and a 2-by-1 vector of
the initial values, defined as [Sigma0; Alpha0], used in the search
algorithm function. For more information, see lsqnonlin.
Data Types: double
Optimization parameters, specified as the comma-separated pair consisting of
'OptimOptions' and a structure defined by using optimoptions.
Data Types: struct
Shift in decimals for the shifted Black model, specified as the comma-separated
pair consisting of 'Shift' and a scalar positive decimal value. Set
this parameter to a positive shift in decimals to add a positive shift to forward rate
and Strike, which effectively sets a negative lower bound for
forward rate and Strike. For example, a Shift
value of 0.01 is equal to a 1% shift.
Data Types: double
Indicator for model used for calibration routine, specified as the
comma-separated pair consisting of 'Model' and a scalar character
vector with a value of normal or
lognormal.
Data Types: char
Output Arguments
Mean reversion value obtained from calibrating the floor using market information, returned as a scalar value.
Volatility value obtained from calibrating the floor using market information, returned as a scalar.
Optimization results, returned as a structure.
More About
A floor consists of a series of put options on interest rates, known as "floorlets."
Each floorlet corresponds to a specific time period (for example, monthly, quarterly) and provides the holder with the right to receive a payment if the reference interest rate (such as LIBOR or SOFR) falls below the floor rate during that period.
Version History
Introduced in R2009aAlthough hwcalbyfloor supports serial date numbers,
datetime values are recommended instead. The
datetime data type provides flexible date and time
formats, storage out to nanosecond precision, and properties to account for time
zones and daylight saving time.
To convert serial date numbers or text to datetime values, use the datetime function. For example:
t = datetime(738427.656845093,"ConvertFrom","datenum"); y = year(t)
y =
2021
There are no plans to remove support for serial date number inputs.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)