estimateFrontier
Estimate specified number of optimal portfolios on the efficient frontier
Description
[ estimates the specified number of
optimal portfolios on the efficient frontier for pwgt,pbuy,psell]
= estimateFrontier(obj)Portfolio,
PortfolioCVaR, or PortfolioMAD objects. For details on
the respective workflows when using these different objects, see Portfolio Object Workflow, PortfolioCVaR Object Workflow, and PortfolioMAD Object Workflow.
Examples
Create efficient portfolios:
load CAPMuniverse p = Portfolio('AssetList',Assets(1:12)); p = estimateAssetMoments(p, Data(:,1:12),'missingdata',true); p = setDefaultConstraints(p); plotFrontier(p);

pwgt = estimateFrontier(p, 5); pnames = cell(1,5); for i = 1:5 pnames{i} = sprintf('Port%d',i); end Blotter = dataset([{pwgt},pnames],'obsnames',p.AssetList); disp(Blotter);
Port1 Port2 Port3 Port4 Port5
AAPL 0.017926 0.058247 0.097816 0.12955 0
AMZN 0 0 0 0 0
CSCO 0 0 0 0 0
DELL 0.0041906 0 0 0 0
EBAY 0 0 0 0 0
GOOG 0.16144 0.35678 0.55228 0.75116 1
HPQ 0.052566 0.032302 0.011186 0 0
IBM 0.46422 0.36045 0.25577 0.11928 0
INTC 0 0 0 0 0
MSFT 0.29966 0.19222 0.082949 0 0
ORCL 0 0 0 0 0
YHOO 0 0 0 0 0
Create a Portfolio object for 12 stocks based on CAPMuniverse.mat.
load CAPMuniverse p0 = Portfolio('AssetList',Assets(1:12)); p0 = estimateAssetMoments(p0, Data(:,1:12),'missingdata',true); p0 = setDefaultConstraints(p0);
Use setMinMaxNumAssets to define a maximum number of 3 assets.
p1 = setMinMaxNumAssets(p0, [], 3);
Use setBounds to define a lower and upper bound and a BoundType of 'Conditional'.
p1 = setBounds(p1, 0.1, 0.5,'BoundType', 'Conditional'); pwgt = estimateFrontier(p1, 5);
The following table shows that the optimized allocations only have maximum 3 assets invested, and small positions less than 0.1 are avoided.
result = table(p0.AssetList', pwgt)
result=12×2 table
Var1 pwgt
________ ___________________________________________________________________
{'AAPL'} 0 0 0 0.14232 0
{'AMZN'} 0 0 0 0 0
{'CSCO'} 0 0 0 0 0
{'DELL'} 0 0 0 0 0
{'EBAY'} 0 0 0 0 0.5
{'GOOG'} 0.16891 0.29534 0.42177 0.5 0.5
{'HPQ' } 0 0 4.996e-15 -2.7756e-17 0
{'IBM' } 0.49968 0.43657 0.37326 0.35768 0
{'INTC'} 0 0 0 0 0
{'MSFT'} 0.3314 0.2681 0.20496 4.6838e-17 0
{'ORCL'} 0 0 0 0 0
{'YHOO'} 0 0 0 0 0
The estimateFrontier function uses the MINLP solver to solve this problem. Use the setSolverMINLP function to configure the SolverType and options.
p1.solverTypeMINLP
ans = 'OuterApproximation'
p1.solverOptionsMINLP
ans = struct with fields:
MaxIterations: 1000
AbsoluteGapTolerance: 1.0000e-07
RelativeGapTolerance: 1.0000e-05
NonlinearScalingFactor: 1000
ObjectiveScalingFactor: 1000
Display: 'off'
CutGeneration: 'basic'
MaxIterationsInactiveCut: 30
ActiveCutTolerance: 1.0000e-07
IntMainSolverOptions: [1×1 optim.options.Intlinprog]
NumIterationsEarlyIntegerConvergence: 30
ExtendedFormulation: 0
NumInnerCuts: 10
NumInitialOuterCuts: 10
Create efficient portfolios:
load CAPMuniverse p = PortfolioCVaR('AssetList',Assets(1:12)); p = simulateNormalScenariosByData(p, Data(:,1:12), 20000 ,'missingdata',true); p = setDefaultConstraints(p); p = setProbabilityLevel(p, 0.95); plotFrontier(p);
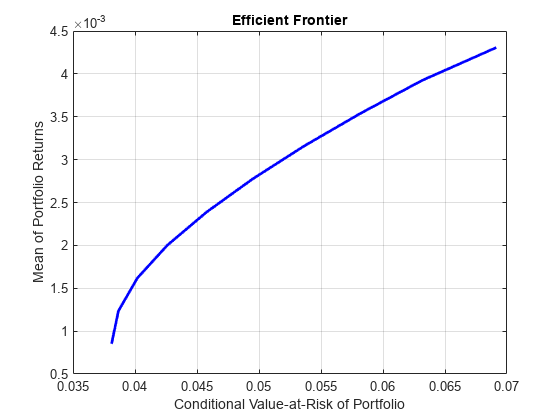
pwgt = estimateFrontier(p, 5); pnames = cell(1,5); for i = 1:5 pnames{i} = sprintf('Port%d',i); end Blotter = dataset([{pwgt},pnames],'obsnames',p.AssetList); disp(Blotter);
Port1 Port2 Port3 Port4 Port5
AAPL 0.010223 0.073393 0.11939 0.13137 0
AMZN 0 0 0 0 0
CSCO 0 0 0 0 0
DELL 0.02301 0 0 0 0
EBAY 0 0 0 0 0
GOOG 0.20389 0.38068 0.56253 0.75919 1
HPQ 0.041396 0.009472 0 0 0
IBM 0.44369 0.36472 0.26247 0.10944 0
INTC 0 0 0 0 0
MSFT 0.27779 0.17174 0.055611 0 0
ORCL 0 0 0 0 0
YHOO 0 0 0 0 0
Create efficient portfolios:
load CAPMuniverse p = PortfolioMAD('AssetList',Assets(1:12)); p = simulateNormalScenariosByData(p, Data(:,1:12), 20000 ,'missingdata',true); p = setDefaultConstraints(p); plotFrontier(p);
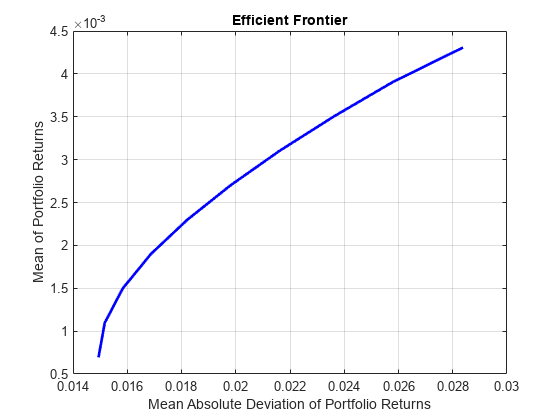
pwgt = estimateFrontier(p, 5); pnames = cell(1,5); for i = 1:5 pnames{i} = sprintf('Port%d',i); end Blotter = dataset([{pwgt},pnames],'obsnames',p.AssetList); disp(Blotter);
Port1 Port2 Port3 Port4 Port5
AAPL 0.029643 0.075874 0.11335 0.13405 0
AMZN 0 0 0 0 0
CSCO 0 0 0 0 0
DELL 0.0086367 0 0 0 0
EBAY 0 0 0 0 0
GOOG 0.16177 0.35217 0.54489 0.74913 1
HPQ 0.056891 0.023419 0 0 0
IBM 0.45916 0.37921 0.29376 0.11682 0
INTC 0 0 0 0 0
MSFT 0.2839 0.16933 0.048005 0 0
ORCL 0 0 0 0 0
YHOO 0 0 0 0 0
Obtain the default number of efficient portfolios over the entire range of the efficient frontier.
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p = setAssetMoments(p, m, C);
p = setDefaultConstraints(p);
pwgt = estimateFrontier(p);
disp(pwgt); 0.8891 0.7215 0.5540 0.3865 0.2190 0.0515 0 0 0 0
0.0369 0.1289 0.2209 0.3129 0.4049 0.4969 0.4049 0.2314 0.0579 0
0.0404 0.0567 0.0730 0.0893 0.1056 0.1219 0.1320 0.1394 0.1468 0
0.0336 0.0929 0.1521 0.2113 0.2705 0.3297 0.4630 0.6292 0.7953 1.0000
Starting from the initial portfolio, the estimateFrontier function returns purchases and sales to get from your initial portfolio to each efficient portfolio on the efficient frontier. Given an initial portfolio in pwgt0, you can obtain purchases and sales.
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
p = Portfolio;
p = setAssetMoments(p, m, C);
p = setDefaultConstraints(p);
pwgt0 = [ 0.3; 0.3; 0.2; 0.1 ];
p = setInitPort(p, pwgt0);
[pwgt, pbuy, psell] = estimateFrontier(p);
display(pwgt);pwgt = 4×10
0.8891 0.7215 0.5540 0.3865 0.2190 0.0515 0 0 0 0
0.0369 0.1289 0.2209 0.3129 0.4049 0.4969 0.4049 0.2314 0.0579 0
0.0404 0.0567 0.0730 0.0893 0.1056 0.1219 0.1320 0.1394 0.1468 0
0.0336 0.0929 0.1521 0.2113 0.2705 0.3297 0.4630 0.6292 0.7953 1.0000
display(pbuy);
pbuy = 4×10
0.5891 0.4215 0.2540 0.0865 0 0 0 0 0 0
0 0 0 0.0129 0.1049 0.1969 0.1049 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0.0521 0.1113 0.1705 0.2297 0.3630 0.5292 0.6953 0.9000
display(psell);
psell = 4×10
0 0 0 0 0.0810 0.2485 0.3000 0.3000 0.3000 0.3000
0.2631 0.1711 0.0791 0 0 0 0 0.0686 0.2421 0.3000
0.1596 0.1433 0.1270 0.1107 0.0944 0.0781 0.0680 0.0606 0.0532 0.2000
0.0664 0.0071 0 0 0 0 0 0 0 0
Obtain the default number of efficient portfolios over the entire range of the efficient frontier.
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;
rng(11);
AssetScenarios = mvnrnd(m, C, 20000);
p = PortfolioCVaR;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);
p = setProbabilityLevel(p, 0.95);
pwgt = estimateFrontier(p);
disp(pwgt); 0.8445 0.6841 0.5148 0.3534 0.1897 0.0303 0 0 0 0
0.0609 0.1429 0.2302 0.3171 0.3987 0.4742 0.3524 0.1803 0 0
0.0458 0.0640 0.0945 0.1081 0.1340 0.1590 0.1738 0.1918 0.2211 0
0.0488 0.1090 0.1606 0.2215 0.2776 0.3365 0.4738 0.6280 0.7789 1.0000
The function rng() resets the random number generator to produce the documented results. It is not necessary to reset the random number generator to simulate scenarios.
Starting from the initial portfolio, the estimateFrontier function returns purchases and sales to get from your initial portfolio to each efficient portfolio on the efficient frontier. Given an initial portfolio in pwgt0, you can obtain purchases and sales.
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;
rng(11);
AssetScenarios = mvnrnd(m, C, 20000);
p = PortfolioCVaR;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);
p = setProbabilityLevel(p, 0.95);
pwgt0 = [ 0.3; 0.3; 0.2; 0.1 ];
p = setInitPort(p, pwgt0);
[pwgt, pbuy, psell] = estimateFrontier(p);
display(pwgt);pwgt = 4×10
0.8445 0.6841 0.5148 0.3534 0.1897 0.0303 0 0 0 0
0.0609 0.1429 0.2302 0.3171 0.3987 0.4742 0.3524 0.1803 0 0
0.0458 0.0640 0.0945 0.1081 0.1340 0.1590 0.1738 0.1918 0.2211 0
0.0488 0.1090 0.1606 0.2215 0.2776 0.3365 0.4738 0.6280 0.7789 1.0000
display(pbuy);
pbuy = 4×10
0.5445 0.3841 0.2148 0.0534 0 0 0 0 0 0
0 0 0 0.0171 0.0987 0.1742 0.0524 0 0 0
0 0 0 0 0 0 0 0 0.0211 0
0 0.0090 0.0606 0.1215 0.1776 0.2365 0.3738 0.5280 0.6789 0.9000
display(psell);
psell = 4×10
0 0 0 0 0.1103 0.2697 0.3000 0.3000 0.3000 0.3000
0.2391 0.1571 0.0698 0 0 0 0 0.1197 0.3000 0.3000
0.1542 0.1360 0.1055 0.0919 0.0660 0.0410 0.0262 0.0082 0 0.2000
0.0512 0 0 0 0 0 0 0 0 0
The function rng() resets the random number generator to produce the documented results. It is not necessary to reset the random number generator to simulate scenarios.
Obtain the default number of efficient portfolios over the entire range of the efficient frontier.
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;
rng(11);
AssetScenarios = mvnrnd(m, C, 20000);
p = PortfolioMAD;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);
pwgt = estimateFrontier(p);
disp(pwgt); 0.8817 0.7150 0.5488 0.3811 0.2173 0.0503 0 0 0 0
0.0435 0.1290 0.2130 0.2987 0.3821 0.4668 0.3614 0.1751 0 0
0.0385 0.0600 0.0826 0.1061 0.1242 0.1477 0.1780 0.2101 0.2267 0
0.0363 0.0960 0.1556 0.2141 0.2764 0.3352 0.4605 0.6148 0.7733 1.0000
The function rng() resets the random number generator to produce the documented results. It is not necessary to reset the random number generator to simulate scenarios.
Starting from the initial portfolio, the estimateFrontier function returns purchases and sales to get from your initial portfolio to each efficient portfolio on the efficient frontier. Given an initial portfolio in pwgt0, you can obtain purchases and sales.
m = [ 0.05; 0.1; 0.12; 0.18 ];
C = [ 0.0064 0.00408 0.00192 0;
0.00408 0.0289 0.0204 0.0119;
0.00192 0.0204 0.0576 0.0336;
0 0.0119 0.0336 0.1225 ];
m = m/12;
C = C/12;
rng(11);
AssetScenarios = mvnrnd(m, C, 20000);
p = PortfolioMAD;
p = setScenarios(p, AssetScenarios);
p = setDefaultConstraints(p);
pwgt0 = [ 0.3; 0.3; 0.2; 0.1 ];
p = setInitPort(p, pwgt0);
[pwgt, pbuy, psell] = estimateFrontier(p);
display(pwgt);pwgt = 4×10
0.8817 0.7150 0.5488 0.3811 0.2173 0.0503 0 0 0 0
0.0435 0.1290 0.2130 0.2987 0.3821 0.4668 0.3614 0.1751 0 0
0.0385 0.0600 0.0826 0.1061 0.1242 0.1477 0.1780 0.2101 0.2267 0
0.0363 0.0960 0.1556 0.2141 0.2764 0.3352 0.4605 0.6148 0.7733 1.0000
display(pbuy);
pbuy = 4×10
0.5817 0.4150 0.2488 0.0811 0 0 0 0 0 0
0 0 0 0 0.0821 0.1668 0.0614 0 0 0
0 0 0 0 0 0 0 0.0101 0.0267 0
0 0 0.0556 0.1141 0.1764 0.2352 0.3605 0.5148 0.6733 0.9000
display(psell);
psell = 4×10
0 0 0 0 0.0827 0.2497 0.3000 0.3000 0.3000 0.3000
0.2565 0.1710 0.0870 0.0013 0 0 0 0.1249 0.3000 0.3000
0.1615 0.1400 0.1174 0.0939 0.0758 0.0523 0.0220 0 0 0.2000
0.0637 0.0040 0 0 0 0 0 0 0 0
The function rng() resets the random number generator to produce the documented results. It is not necessary to reset the random number generator to simulate scenarios.
Input Arguments
Object for portfolio, specified using Portfolio,
PortfolioCVaR, or PortfolioMAD object. For more
information on creating a portfolio object, see
Data Types: object
Number of points to obtain on the efficient frontier, specified as a scalar integer.
Note
If no value is specified for NumPorts, the default value is obtained
from the hidden property defaultNumPorts (default value is
10). If NumPorts = 1, this
function returns the portfolio specified by the hidden property
defaultFrontierLimit (current default value is
'min').
Data Types: double
Output Arguments
Optimal portfolios on the efficient frontier with specified number of portfolios spaced
equally from minimum to maximum portfolio return, returned as a
NumAssets-by-NumPorts matrix. pwgt
is returned for a Portfolio, PortfolioCVaR, or
PortfolioMAD input object (obj).
Purchases relative to an initial portfolio for optimal portfolios on the efficient
frontier, returned as NumAssets-by-NumPorts matrix.
Note
If no initial portfolio is specified in obj.InitPort, that value is
assumed to be 0 such that pbuy = max(0, pwgt) and
psell = max(0, -pwgt).
pbuy is returned for a Portfolio,
PortfolioCVaR, or PortfolioMAD input object
(obj).
Sales relative to an initial portfolio for optimal portfolios on the efficient frontier,
returned as a NumAssets-by-NumPorts matrix.
Note
If no initial portfolio is specified in obj.InitPort, that value is
assumed to be 0 such that pbuy = max(0, pwgt) and
psell = max(0, -pwgt).
psell is returned for Portfolio,
PortfolioCVaR, or PortfolioMAD input object
(obj).
More About
The efficient frontier is a key concept in modern portfolio theory (MPT) that represents a set of optimal portfolios offering the highest expected return for a given level of risk, or the lowest risk for a given level of expected return.
The efficient frontier illustrates the tradeoff between risk (often measured as the standard deviation of portfolio returns) and expected return. Investors aim to construct portfolios that lie on this frontier to maximize their returns for a given level of risk. Portfolios that lie on the efficient frontier are considered optimal because they provide the best possible expected return for their level of risk. Portfolios that lie below the frontier are suboptimal, as they do not provide sufficient return for the amount of risk taken. The efficient frontier emphasizes the importance of diversification. By combining different assets with varying returns and risks, investors can reduce the overall risk of the portfolio without sacrificing expected returns.
Tips
You can also use dot notation to estimate the specified number of optimal portfolios over the entire efficient frontier.
[pwgt, pbuy, psell] = obj.estimateFrontier(NumPorts);
When introducing transaction costs and turnover constraints to the
Portfolio,PortfolioCVaR, orPortfolioMADobject, the portfolio optimization objective contains a term with an absolute value. For more information on how Financial Toolbox™ handles such cases algorithmically, see References.
References
[1] Cornuejols, G., and R. Tutuncu. Optimization Methods in Finance. Cambridge University Press, 2007.
Version History
Introduced in R2011a
See Also
estimateFrontierByReturn | estimateFrontierByRisk | estimateFrontierLimits | setBounds | setMinMaxNumAssets
Topics
- Estimate Efficient Portfolios for Entire Efficient Frontier for Portfolio Object
- Estimate Efficient Frontiers for Portfolio Object
- Estimate Efficient Portfolios for Entire Frontier for PortfolioCVaR Object
- Estimate Efficient Frontiers for PortfolioCVaR Object
- Estimate Efficient Portfolios Along the Entire Frontier for PortfolioMAD Object
- Estimate Efficient Frontiers for PortfolioMAD Object
- Portfolio Optimization Examples Using Financial Toolbox
- Bond Portfolio Optimization Using Portfolio Object
- Portfolio Optimization Theory
- Choose MINLP Solvers for Portfolio Problems
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)