autobinning

Perform automatic binning of given predictors

Syntax

sc = autobinning(sc)

sc = autobinning(sc,PredictorNames)

sc = autobinning(___,Name,Value)

Description

sc = autobinning(sc) performs automatic binning of all predictors.

Automatic binning finds binning maps or rules to bin numeric data and to group categories of categorical data. The binning rules are stored in the creditscorecard object. To apply the binning rules to the creditscorecard object data, or to a new dataset, use bindata.

sc = autobinning(sc,PredictorNames) performs automatic binning of the predictors given in PredictorNames.

Automatic binning finds binning maps or rules to bin numeric data and to group categories of categorical data. The binning rules are stored in the creditscorecard object. To apply the binning rules to the creditscorecard object data, or to a new dataset, use bindata.

sc = autobinning(___,Name,Value) performs automatic binning of the predictors given in PredictorNames using optional name-value pair arguments. See the name-value argument Algorithm for a description of the supported binning algorithms.

Automatic binning finds binning maps or rules to bin numeric data and to group categories of categorical data. The binning rules are stored in the creditscorecard object. To apply the binning rules to the creditscorecard object data, or to a new dataset, use bindata.

Examples

Perform Automatic Binning Using the Defaults

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).

load CreditCardData
sc = creditscorecard(data,'IDVar','CustID');

Perform automatic binning using the default options. By default, autobinning bins all predictors and uses the Monotone algorithm.

sc = autobinning(sc);

Use bininfo to display the binned data for the predictor CustAge.

bi = bininfo(sc, 'CustAge')

bi=8×6 table
         Bin         Good    Bad     Odds        WOE       InfoValue
    _____________    ____    ___    ______    _________    _________

    {'[-Inf,33)'}     70      53    1.3208     -0.42622     0.019746
    {'[33,37)'  }     64      47    1.3617     -0.39568     0.015308
    {'[37,40)'  }     73      47    1.5532     -0.26411    0.0072573
    {'[40,46)'  }    174      94    1.8511    -0.088658     0.001781
    {'[46,48)'  }     61      25      2.44      0.18758    0.0024372
    {'[48,58)'  }    263     105    2.5048      0.21378     0.013476
    {'[58,Inf]' }     98      26    3.7692      0.62245       0.0352
    {'Totals'   }    803     397    2.0227          NaN     0.095205

Use plotbins to display the histogram and WOE curve for the predictor CustAge.

plotbins(sc,'CustAge')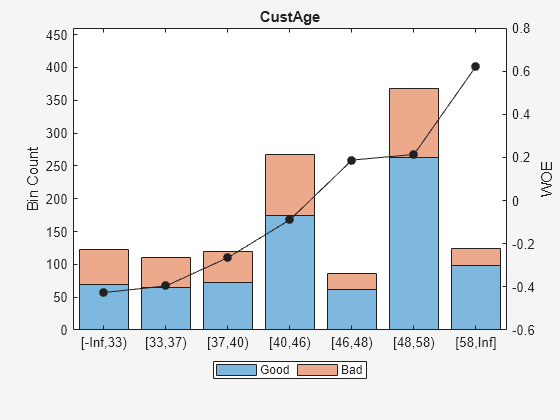

Perform Automatic Binning with a Named Predictor Using the Defaults

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).

load CreditCardData 
sc = creditscorecard(data);

Perform automatic binning for the predictor CustIncome using the default options. By default, autobinning uses the Monotone algorithm.

sc = autobinning(sc,'CustIncome');

Use bininfo to display the binned data.

bi = bininfo(sc, 'CustIncome')

bi=8×6 table
           Bin           Good    Bad     Odds         WOE       InfoValue 
    _________________    ____    ___    _______    _________    __________

    {'[-Inf,29000)' }     53      58    0.91379     -0.79457       0.06364
    {'[29000,33000)'}     74      49     1.5102     -0.29217     0.0091366
    {'[33000,35000)'}     68      36     1.8889     -0.06843    0.00041042
    {'[35000,40000)'}    193      98     1.9694    -0.026696    0.00017359
    {'[40000,42000)'}     68      34          2    -0.011271    1.0819e-05
    {'[42000,47000)'}    164      66     2.4848      0.20579     0.0078175
    {'[47000,Inf]'  }    183      56     3.2679      0.47972      0.041657
    {'Totals'       }    803     397     2.0227          NaN       0.12285

Perform Automatic Binning Using Two Name-Value Pair Arguments

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).

load CreditCardData 
sc = creditscorecard(data);

Perform automatic binning for the predictor CustIncome using the Monotone algorithm with the initial number of bins set to 20. This example explicitly sets both the Algorithm and the AlgorithmOptions name-value arguments.

AlgoOptions = {'InitialNumBins',20}; 
sc = autobinning(sc,'CustIncome','Algorithm','Monotone','AlgorithmOptions',...
     AlgoOptions);

Use bininfo to display the binned data. Here, the cut points, which delimit the bins, are also displayed.

[bi,cp] = bininfo(sc,'CustIncome')

bi=11×6 table
           Bin           Good    Bad     Odds         WOE       InfoValue 
    _________________    ____    ___    _______    _________    __________

    {'[-Inf,19000)' }      2       3    0.66667      -1.1099     0.0056227
    {'[19000,29000)'}     51      55    0.92727     -0.77993      0.058516
    {'[29000,31000)'}     29      26     1.1154     -0.59522      0.017486
    {'[31000,34000)'}     80      42     1.9048    -0.060061     0.0003704
    {'[34000,35000)'}     33      17     1.9412    -0.041124     7.095e-05
    {'[35000,40000)'}    193      98     1.9694    -0.026696    0.00017359
    {'[40000,42000)'}     68      34          2    -0.011271    1.0819e-05
    {'[42000,43000)'}     39      16     2.4375      0.18655      0.001542
    {'[43000,47000)'}    125      50        2.5      0.21187     0.0062972
    {'[47000,Inf]'  }    183      56     3.2679      0.47972      0.041657
    {'Totals'       }    803     397     2.0227          NaN       0.13175

cp = 9×1

       19000
       29000
       31000
       34000
       35000
       40000
       42000
       43000
       47000

Perform Automatic Binning Using Multiple Name-Value Pair Arguments

This example shows how to use the autobinning default Monotone algorithm and the AlgorithmOptions name-value pair arguments associated with the Monotone algorithm. The AlgorithmOptions for the Monotone algorithm are three name-value pair parameters: ‘InitialNumBins', 'Trend', and 'SortCategories'. 'InitialNumBins' and 'Trend' are applicable for numeric predictors and 'Trend' and 'SortCategories' are applicable for categorical predictors.

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).

load CreditCardData
sc = creditscorecard(data,'IDVar','CustID');

Perform automatic binning for the numeric predictor CustIncome using the Monotone algorithm with 20 bins. This example explicitly sets both the Algorithm argument and the AlgorithmOptions name-value arguments for 'InitialNumBins' and 'Trend'.

AlgoOptions = {'InitialNumBins',20,'Trend','Increasing'};

sc = autobinning(sc,'CustIncome','Algorithm','Monotone',...
    'AlgorithmOptions',AlgoOptions);

Use bininfo to display the binned data.

bi = bininfo(sc,'CustIncome')

bi=11×6 table
           Bin           Good    Bad     Odds         WOE       InfoValue 
    _________________    ____    ___    _______    _________    __________

    {'[-Inf,19000)' }      2       3    0.66667      -1.1099     0.0056227
    {'[19000,29000)'}     51      55    0.92727     -0.77993      0.058516
    {'[29000,31000)'}     29      26     1.1154     -0.59522      0.017486
    {'[31000,34000)'}     80      42     1.9048    -0.060061     0.0003704
    {'[34000,35000)'}     33      17     1.9412    -0.041124     7.095e-05
    {'[35000,40000)'}    193      98     1.9694    -0.026696    0.00017359
    {'[40000,42000)'}     68      34          2    -0.011271    1.0819e-05
    {'[42000,43000)'}     39      16     2.4375      0.18655      0.001542
    {'[43000,47000)'}    125      50        2.5      0.21187     0.0062972
    {'[47000,Inf]'  }    183      56     3.2679      0.47972      0.041657
    {'Totals'       }    803     397     2.0227          NaN       0.13175

Perform Automatic Binning for Multiple Predictors

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).

load CreditCardData 
sc = creditscorecard(data,'IDVar','CustID');

Perform automatic binning for the predictor CustIncome and CustAge using the default Monotone algorithm with AlgorithmOptions for InitialNumBins and Trend.

AlgoOptions = {'InitialNumBins',20,'Trend','Increasing'};

sc = autobinning(sc,{'CustAge','CustIncome'},'Algorithm','Monotone',...
    'AlgorithmOptions',AlgoOptions);

Use bininfo to display the binned data.

bi1 = bininfo(sc, 'CustIncome')

bi1=11×6 table
           Bin           Good    Bad     Odds         WOE       InfoValue 
    _________________    ____    ___    _______    _________    __________

    {'[-Inf,19000)' }      2       3    0.66667      -1.1099     0.0056227
    {'[19000,29000)'}     51      55    0.92727     -0.77993      0.058516
    {'[29000,31000)'}     29      26     1.1154     -0.59522      0.017486
    {'[31000,34000)'}     80      42     1.9048    -0.060061     0.0003704
    {'[34000,35000)'}     33      17     1.9412    -0.041124     7.095e-05
    {'[35000,40000)'}    193      98     1.9694    -0.026696    0.00017359
    {'[40000,42000)'}     68      34          2    -0.011271    1.0819e-05
    {'[42000,43000)'}     39      16     2.4375      0.18655      0.001542
    {'[43000,47000)'}    125      50        2.5      0.21187     0.0062972
    {'[47000,Inf]'  }    183      56     3.2679      0.47972      0.041657
    {'Totals'       }    803     397     2.0227          NaN       0.13175

bi2 = bininfo(sc, 'CustAge')

bi2=8×6 table
         Bin         Good    Bad     Odds        WOE       InfoValue 
    _____________    ____    ___    ______    _________    __________

    {'[-Inf,35)'}     93      76    1.2237     -0.50255      0.038003
    {'[35,40)'  }    114      71    1.6056      -0.2309     0.0085141
    {'[40,42)'  }     52      30    1.7333     -0.15437     0.0016687
    {'[42,44)'  }     58      32    1.8125     -0.10971    0.00091888
    {'[44,47)'  }     97      51     1.902    -0.061533    0.00047174
    {'[47,62)'  }    333     130    2.5615      0.23619      0.020605
    {'[62,Inf]' }     56       7         8        1.375      0.071647
    {'Totals'   }    803     397    2.0227          NaN       0.14183

Perform Automatic Binning for a Categorical Predictor Using the Defaults

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).

load CreditCardData 
sc = creditscorecard(data);

Perform automatic binning for the predictor that is a categorical predictor called ResStatus using the default options. By default, autobinning uses the Monotone algorithm.

sc = autobinning(sc,'ResStatus');

Use bininfo to display the binned data.

bi = bininfo(sc, 'ResStatus')

bi=4×6 table
         Bin          Good    Bad     Odds        WOE       InfoValue
    ______________    ____    ___    ______    _________    _________

    {'Tenant'    }    307     167    1.8383    -0.095564    0.0036638
    {'Home Owner'}    365     177    2.0621     0.019329    0.0001682
    {'Other'     }    131      53    2.4717      0.20049    0.0059418
    {'Totals'    }    803     397    2.0227          NaN    0.0097738

Perform Automatic Binning for a Categorical Predictor Using Name-Value Pair Arguments

This example shows how to modify the data (for this example only) to illustrate binning categorical predictors using the Monotone algorithm.

Create a creditscorecard object using the CreditCardData.mat file to load the data (using a dataset from Refaat 2011).

load CreditCardData

Add two new categories and updating the response variable.

newdata = data;
rng('default'); %for reproducibility
Predictor = 'ResStatus';
Status    = newdata.status;
NumObs    = length(newdata.(Predictor));
Ind1 = randi(NumObs,100,1);
Ind2 = randi(NumObs,100,1);
newdata.(Predictor)(Ind1) = 'Subtenant';
newdata.(Predictor)(Ind2) = 'CoOwner';
Status(Ind1) = randi(2,100,1)-1;
Status(Ind2) = randi(2,100,1)-1;

newdata.status = Status;

Update the creditscorecard object using the newdata and plot the bins for a later comparison.

scnew = creditscorecard(newdata,'IDVar','CustID');
[bi,cg] = bininfo(scnew,Predictor)

bi=6×6 table
         Bin          Good    Bad     Odds       WOE       InfoValue
    ______________    ____    ___    ______    ________    _________

    {'Home Owner'}    308     154         2    0.092373    0.0032392
    {'Tenant'    }    264     136    1.9412     0.06252    0.0012907
    {'Other'     }    109      49    2.2245     0.19875    0.0050386
    {'Subtenant' }     42      42         1    -0.60077     0.026813
    {'CoOwner'   }     52      44    1.1818    -0.43372     0.015802
    {'Totals'    }    775     425    1.8235         NaN     0.052183

cg=5×2 table
       Category       BinNumber
    ______________    _________

    {'Home Owner'}        1    
    {'Tenant'    }        2    
    {'Other'     }        3    
    {'Subtenant' }        4    
    {'CoOwner'   }        5    

plotbins(scnew,Predictor)

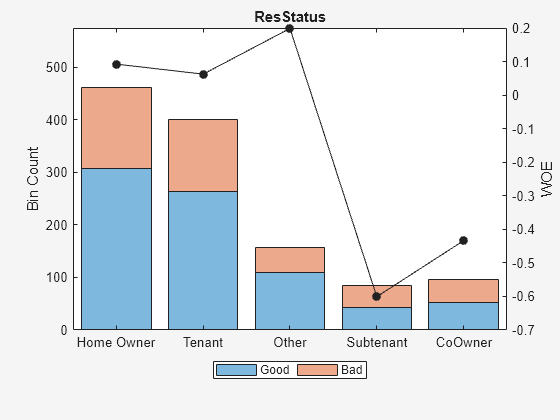
Perform automatic binning for the categorical Predictor using the default Monotone algorithm with the AlgorithmOptions name-value pair arguments for 'SortCategories' and 'Trend'.

AlgoOptions = {'SortCategories','Goods','Trend','Increasing'};

scnew = autobinning(scnew,Predictor,'Algorithm','Monotone',...
    'AlgorithmOptions',AlgoOptions);

Use bininfo to display the bin information. The second output parameter 'cg' captures the bin membership, which is the bin number that each group belongs to.

[bi,cg] = bininfo(scnew,Predictor)

bi=4×6 table
       Bin        Good    Bad     Odds       WOE       InfoValue
    __________    ____    ___    ______    ________    _________

    {'Group1'}     42      42         1    -0.60077     0.026813
    {'Group2'}     52      44    1.1818    -0.43372     0.015802
    {'Group3'}    681     339    2.0088    0.096788    0.0078459
    {'Totals'}    775     425    1.8235         NaN      0.05046

cg=5×2 table
       Category       BinNumber
    ______________    _________

    {'Subtenant' }        1    
    {'CoOwner'   }        2    
    {'Other'     }        3    
    {'Tenant'    }        3    
    {'Home Owner'}        3    

Plot bins and compare with the histogram plotted pre-binning.

plotbins(scnew,Predictor)

Perform Automatic Binning When Using Missing Data

Create a creditscorecard object using the CreditCardData.mat file to load the dataMissing with missing values.

load CreditCardData.mat 
head(dataMissing,5)

    CustID    CustAge    TmAtAddress     ResStatus     EmpStatus    CustIncome    TmWBank    OtherCC    AMBalance    UtilRate    status
    ______    _______    ___________    ___________    _________    __________    _______    _______    _________    ________    ______

      1          53          62         <undefined>    Unknown        50000         55         Yes       1055.9        0.22        0   
      2          61          22         Home Owner     Employed       52000         25         Yes       1161.6        0.24        0   
      3          47          30         Tenant         Employed       37000         61         No        877.23        0.29        0   
      4         NaN          75         Home Owner     Employed       53000         20         Yes       157.37        0.08        0   
      5          68          56         Home Owner     Employed       53000         14         Yes       561.84        0.11        0   

fprintf('Number of rows: %d\n',height(dataMissing))

Number of rows: 1200

fprintf('Number of missing values CustAge: %d\n',sum(ismissing(dataMissing.CustAge)))

Number of missing values CustAge: 30

fprintf('Number of missing values ResStatus: %d\n',sum(ismissing(dataMissing.ResStatus)))

Number of missing values ResStatus: 40

Use creditscorecard with the name-value argument 'BinMissingData' set to true to bin the missing numeric and categorical data in a separate bin.

sc = creditscorecard(dataMissing,'BinMissingData',true);
disp(sc)

  creditscorecard with properties:

                GoodLabel: 0
              ResponseVar: 'status'
               WeightsVar: ''
                 VarNames: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'  'status'}
        NumericPredictors: {'CustID'  'CustAge'  'TmAtAddress'  'CustIncome'  'TmWBank'  'AMBalance'  'UtilRate'}
    CategoricalPredictors: {'ResStatus'  'EmpStatus'  'OtherCC'}
           BinMissingData: 1
                    IDVar: ''
            PredictorVars: {'CustID'  'CustAge'  'TmAtAddress'  'ResStatus'  'EmpStatus'  'CustIncome'  'TmWBank'  'OtherCC'  'AMBalance'  'UtilRate'}
                     Data: [1200×11 table]

Perform automatic binning using the Merge algorithm.

sc = autobinning(sc,'Algorithm','Merge'); 

Display bin information for numeric data for 'CustAge' that includes missing data in a separate bin labelled <missing> and this is the last bin. No matter what binning algorithm is used in autobinning, the algorithm operates on the non-missing data and the bin for the <missing> numeric values for a predictor is always the last bin.

[bi,cp] = bininfo(sc,'CustAge'); 
disp(bi) 

         Bin         Good    Bad     Odds        WOE       InfoValue 
    _____________    ____    ___    _______    ________    __________

    {'[-Inf,32)'}     56      39     1.4359    -0.34263     0.0097643
    {'[32,33)'  }     13      13          1    -0.70442      0.011663
    {'[33,34)'  }      9      11    0.81818    -0.90509      0.014934
    {'[34,65)'  }    677     317     2.1356    0.054351      0.002424
    {'[65,Inf]' }     29       6     4.8333     0.87112      0.018295
    {'<missing>'}     19      11     1.7273    -0.15787    0.00063885
    {'Totals'   }    803     397     2.0227         NaN      0.057718

plotbins(sc,'CustAge')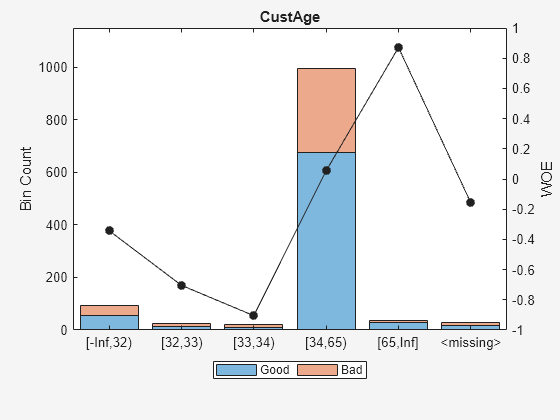

Display bin information for categorical data for 'ResStatus' that includes missing data in a separate bin labelled <missing> and this is the last bin. No matter what binning algorithm is used in autobinning, the algorithm operates on the non-missing data and the bin for the <missing> categorical values for a predictor is always the last bin.

[bi,cg] = bininfo(sc,'ResStatus');
disp(bi)

         Bin         Good    Bad     Odds        WOE       InfoValue 
    _____________    ____    ___    ______    _________    __________

    {'Group1'   }    648     332    1.9518    -0.035663     0.0010449
    {'Group2'   }    128      52    2.4615      0.19637     0.0055808
    {'<missing>'}     27      13    2.0769     0.026469    2.3248e-05
    {'Totals'   }    803     397    2.0227          NaN     0.0066489

plotbins(sc,'ResStatus')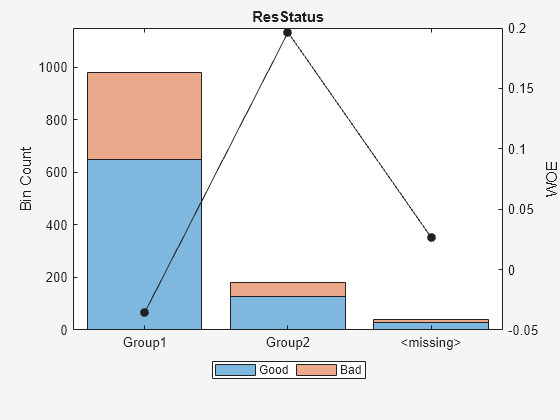

Perform Automatic Binning Using the Split Algorithm

This example demonstrates using the 'Split' algorithm with categorical and numeric predictors. Load the CreditCardData.mat dataset and modify so that it contains four categories for the predictor 'ResStatus' to demonstrate how the split algorithm works.

load CreditCardData.mat
x = data.ResStatus;
Ind = find(x == 'Tenant');
Nx  = length(Ind);
x(Ind(1:floor(Nx/3))) = 'Subletter';
data.ResStatus = x;

Create a creditscorecard and use bininfo to display the 'Statistics'.

sc = creditscorecard(data,'IDVar','CustID');
[bi1,cg1] = bininfo(sc,'ResStatus','Statistics',{'Odds','WOE','InfoValue'});
disp(bi1)

         Bin          Good    Bad     Odds        WOE       InfoValue 
    ______________    ____    ___    ______    _________    __________

    {'Home Owner'}    365     177    2.0621     0.019329     0.0001682
    {'Tenant'    }    204     112    1.8214      -0.1048     0.0029415
    {'Other'     }    131      53    2.4717      0.20049     0.0059418
    {'Subletter' }    103      55    1.8727    -0.077023    0.00079103
    {'Totals'    }    803     397    2.0227          NaN     0.0098426

disp(cg1)

       Category       BinNumber
    ______________    _________

    {'Home Owner'}        1    
    {'Tenant'    }        2    
    {'Other'     }        3    
    {'Subletter' }        4    

Using the Split Algorithm with a Categorical Predictor

Apply presorting to the 'ResStatus' category using the default sorting by 'Odds' and specify the 'Split' algorithm.

sc = autobinning(sc,'ResStatus', 'Algorithm', 'split','AlgorithmOptions',...
    {'Measure','gini','SortCategories','odds','Tolerance',1e4});
[bi2,cg2] = bininfo(sc,'ResStatus','Statistics',{'Odds','WOE','InfoValue'});
disp(bi2)

       Bin        Good    Bad     Odds     WOE    InfoValue
    __________    ____    ___    ______    ___    _________

    {'Group1'}    803     397    2.0227      0        0    
    {'Totals'}    803     397    2.0227    NaN        0    

disp(cg2)

       Category       BinNumber
    ______________    _________

    {'Tenant'    }        1    
    {'Subletter' }        1    
    {'Home Owner'}        1    
    {'Other'     }        1    

Using the Split Algorithm with a Numeric Predictor

To demonstrate a split for the numeric predictor, 'TmAtAddress', first use autobinning with the default 'Monotone' algorithm.

sc = autobinning(sc,'TmAtAddress');
bi3 = bininfo(sc,'TmAtAddress','Statistics',{'Odds','WOE','InfoValue'});
disp(bi3)

         Bin         Good    Bad     Odds        WOE       InfoValue 
    _____________    ____    ___    ______    _________    __________

    {'[-Inf,23)'}    239     129    1.8527    -0.087767     0.0023963
    {'[23,83)'  }    480     232     2.069      0.02263    0.00030269
    {'[83,Inf]' }     84      36    2.3333      0.14288       0.00199
    {'Totals'   }    803     397    2.0227          NaN      0.004689

Then use autobinning with the 'Split' algorithm.

sc = autobinning(sc,'TmAtAddress','Algorithm', 'Split');
bi4 = bininfo(sc,'TmAtAddress','Statistics',{'Odds','WOE','InfoValue'});
disp(bi4)

        Bin         Good    Bad     Odds         WOE       InfoValue 
    ____________    ____    ___    _______    _________    __________

    {'[-Inf,4)'}     20      12     1.6667     -0.19359     0.0010299
    {'[4,5)'   }      4       7    0.57143       -1.264      0.015991
    {'[5,23)'  }    215     110     1.9545    -0.034261    0.00031973
    {'[23,33)' }    130      39     3.3333      0.49955        0.0318
    {'[33,Inf]'}    434     229     1.8952    -0.065096     0.0023664
    {'Totals'  }    803     397     2.0227          NaN      0.051507

Perform Automatic Binning Using the Merge Algorithm

Load the CreditCardData.mat dataset. This example demonstrates using the 'Merge' algorithm with categorical and numeric predictors.

load CreditCardData.mat

Using the Merge Algorithm with a Categorical Predictor

To merge a categorical predictor, create a creditscorecard using default sorting by 'Odds' and then use bininfo on the categorical predictor 'ResStatus'.

sc = creditscorecard(data,'IDVar','CustID');
[bi1,cg1] = bininfo(sc,'ResStatus','Statistics',{'Odds','WOE','InfoValue'});
disp(bi1);

         Bin          Good    Bad     Odds        WOE       InfoValue
    ______________    ____    ___    ______    _________    _________

    {'Home Owner'}    365     177    2.0621     0.019329    0.0001682
    {'Tenant'    }    307     167    1.8383    -0.095564    0.0036638
    {'Other'     }    131      53    2.4717      0.20049    0.0059418
    {'Totals'    }    803     397    2.0227          NaN    0.0097738

disp(cg1);

       Category       BinNumber
    ______________    _________

    {'Home Owner'}        1    
    {'Tenant'    }        2    
    {'Other'     }        3    

Use autobinning and specify the 'Merge' algorithm.

sc = autobinning(sc,'ResStatus','Algorithm', 'Merge');
[bi2,cg2] = bininfo(sc,'ResStatus','Statistics',{'Odds','WOE','InfoValue'});
disp(bi2)

       Bin        Good    Bad     Odds        WOE       InfoValue
    __________    ____    ___    ______    _________    _________

    {'Group1'}    672     344    1.9535    -0.034802    0.0010314
    {'Group2'}    131      53    2.4717      0.20049    0.0059418
    {'Totals'}    803     397    2.0227          NaN    0.0069732

disp(cg2)

       Category       BinNumber
    ______________    _________

    {'Tenant'    }        1    
    {'Home Owner'}        1    
    {'Other'     }        2    

Using the Merge Algorithm with a Numeric Predictor

To demonstrate a merge for the numeric predictor, 'TmAtAddress', first use autobinning with the default 'Monotone' algorithm.

sc = autobinning(sc,'TmAtAddress');
bi3 = bininfo(sc,'TmAtAddress','Statistics',{'Odds','WOE','InfoValue'});
disp(bi3)

         Bin         Good    Bad     Odds        WOE       InfoValue 
    _____________    ____    ___    ______    _________    __________

    {'[-Inf,23)'}    239     129    1.8527    -0.087767     0.0023963
    {'[23,83)'  }    480     232     2.069      0.02263    0.00030269
    {'[83,Inf]' }     84      36    2.3333      0.14288       0.00199
    {'Totals'   }    803     397    2.0227          NaN      0.004689

Then use autobinning with the 'Merge' algorithm.

sc = autobinning(sc,'TmAtAddress','Algorithm', 'Merge');
bi4 = bininfo(sc,'TmAtAddress','Statistics',{'Odds','WOE','InfoValue'});
disp(bi4)

         Bin         Good    Bad     Odds         WOE       InfoValue 
    _____________    ____    ___    _______    _________    __________

    {'[-Inf,28)'}    303     152     1.9934    -0.014566    8.0646e-05
    {'[28,30)'  }     27       2       13.5       1.8983      0.054264
    {'[30,98)'  }    428     216     1.9815    -0.020574    0.00022794
    {'[98,106)' }     11      13    0.84615     -0.87147      0.016599
    {'[106,Inf]'}     34      14     2.4286      0.18288     0.0012942
    {'Totals'   }    803     397     2.0227          NaN      0.072466

Input Arguments

sc — Credit scorecard model

creditscorecard object

Credit scorecard model, specified as a creditscorecard object. Use creditscorecard to create a creditscorecard object.

PredictorNames — Predictor or predictors names to automatically bin

character vector | cell array of character vectors

Predictor or predictors names to automatically bin, specified as a character vector or a cell array of character vectors containing the name of the predictor or predictors. PredictorNames are case-sensitive and when no PredictorNames are defined, all predictors in the PredictorVars property of the creditscorecard object are binned.

Data Types: char | cell

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: sc = autobinning(sc,'Algorithm','EqualFrequency')

Algorithm — Algorithm selection

'Monotone' (default) | character vector with values 'Monotone', 'Split', 'Merge', 'EqualFrequency', 'EqualWidth'

Algorithm selection, specified as the comma-separated pair consisting of 'Algorithm' and a character vector indicating which algorithm to use. The same algorithm is used for all predictors in PredictorNames. Possible values are:

• 'Monotone' — (default) Monotone Adjacent Pooling Algorithm (MAPA), also known as Maximum Likelihood Monotone Coarse Classifier (MLMCC). Supervised optimal binning algorithm that aims to find bins with a monotone Weight-Of-Evidence (WOE) trend. This algorithm assumes that only neighboring attributes can be grouped. Thus, for categorical predictors, categories are sorted before applying the algorithm (see 'SortCategories' option for AlgorithmOptions). For more information, see Monotone.

• 'Split' — Supervised binning algorithm, where a measure is used to split the data into bins. The measures supported by 'Split' are gini, chi2, infovalue, and entropy. The resulting split must be such that the gain in the information function is maximized. For more information on these measures, see AlgorithmOptions and Split.

• 'Merge' — Supervised automatic binning algorithm, where a measure is used to merge bins into buckets. The measures supported by 'Merge' are chi2, gini, infovalue, and entropy. The resulting merging must be such that any pair of adjacent bins is statistically different from each other, according to the chosen measure. For more information on these measures, see AlgorithmOptions and Merge.

• 'EqualFrequency' — Unsupervised algorithm that divides the data into a predetermined number of bins that contain approximately the same number of observations. This algorithm is also known as “equal height” or “equal depth.” For categorical predictors, categories are sorted before applying the algorithm (see 'SortCategories' option for AlgorithmOptions). For more information, see Equal Frequency.

• 'EqualWidth' — Unsupervised algorithm that divides the range of values in the domain of the predictor variable into a predetermined number of bins of “equal width.” For numeric data, the width is measured as the distance between bin edges. For categorical data, width is measured as the number of categories within a bin. For categorical predictors, categories are sorted before applying the algorithm (see 'SortCategories' option for AlgorithmOptions). For more information, see Equal Width.

Data Types: char

AlgorithmOptions — Algorithm options for selected Algorithm

{'InitialNumBins',10,'Trend','Auto','SortCategories','Odds'} for Monotone (default) | cell array with {'OptionName',OptionValue} for Algorithm options

Algorithm options for the selected Algorithm, specified as the comma-separated pair consisting of 'AlgorithmOptions' and a cell array. Possible values are:

• For Monotone algorithm:

  • {'InitialNumBins',n} — Initial number (n) of bins (default is 10). 'InitialNumBins' must be an integer > 2. Used for numeric predictors only.

  • {'Trend','TrendOption'} — Determines whether the Weight-Of-Evidence (WOE) monotonic trend is expected to be increasing or decreasing. The values for 'TrendOption' are:

    • 'Auto' — (Default) Automatically determines if the WOE trend is increasing or decreasing.

    • 'Increasing' — Look for an increasing WOE trend.

    • 'Decreasing' — Look for a decreasing WOE trend.

    The value of the optional input parameter 'Trend' does not necessarily reflect that of the resulting WOE curve. The parameter 'Trend' tells the algorithm to “look for” an increasing or decreasing trend, but the outcome may not show the desired trend. For example, the algorithm cannot find a decreasing trend when the data actually has an increasing WOE trend. For more information on the 'Trend' option, see Monotone.

  • {'SortCategories','SortOption'} — Used for categorical predictors only. Used to determine how the predictor categories are sorted as a preprocessing step before applying the algorithm. The values of 'SortOption' are:

    • 'Odds' — (default) The categories are sorted by order of increasing values of odds, defined as the ratio of “Good” to “Bad” observations, for the given category.

    • 'Goods' — The categories are sorted by order of increasing values of “Good.”

    • 'Bads' — The categories are sorted by order of increasing values of “Bad.”

    • 'Totals' — The categories are sorted by order of increasing values of total number of observations (“Good” plus “Bad”).

    • 'None' — No sorting is applied. The existing order of the categories is unchanged before applying the algorithm. (The existing order of the categories can be seen in the category grouping optional output from bininfo.)

    For more information, see Sort Categories

• For Split algorithm:

  • {'InitialNumBins',n} — Specifies an integer that determines the number (n >0) of bins that the predictor is initially binned into before splitting. Valid for numeric predictors only. Default is 50.

  • {'Measure',MeasureName} — Specifies the measure where 'MeasureName' is one of the following:'Gini' (default), 'Chi2', 'InfoValue', or 'Entropy'.

  • {'MinBad',n} — Specifies the minimum number n (n>=0) of Bads per bin. The default value is 1, to avoid pure bins.

  • {'MaxBad',n} — Specifies the maximum number n (n>=0) of Bads per bin. The default value is Inf.

  • {'MinGood',n} — Specifies the minimum number n (n>=0) of Goods per bin. The default value is 1, to avoid pure bins.

  • {'MaxGood',n} — Specifies the maximum number n (n>=0) of Goods per bin. The default value is Inf.

  • {'MinCount',n} — Specifies the minimum number n (n>=0) of observations per bin. The default value is 1, to avoid empty bins.

  • {'MaxCount',n} — Specifies the maximum number n (n>=0) of observations per bin. The default value is Inf.

  • {'MaxNumBins',n} — Specifies the maximum number n (n>=2) of bins resulting from the splitting. The default value is 5.

  • {'Tolerance',Tol} — Specifies the minimum gain (>0) in the information function, during the iteration scheme, to select the cut-point that maximizes the gain. The default is 1e4.

  • {'Significance',n} — Significance level threshold for the chi-square statistic, above which splitting happens. Values are in the interval [0,1]. Default is 0.9 (90% significance level).

  • {'SortCategories','SortOption'} — Used for categorical predictors only. Used to determine how the predictor categories are sorted as a preprocessing step before applying the algorithm. The values of 'SortOption' are:

    • 'Goods' — The categories are sorted by order of increasing values of “Good.”

    • 'Bads' — The categories are sorted by order of increasing values of “Bad.”

    • 'Odds' — (default) The categories are sorted by order of increasing values of odds, defined as the ratio of “Good” to “Bad” observations, for the given category.

    • 'Totals' — The categories are sorted by order of increasing values of total number of observations (“Good” plus “Bad”).

    • 'None' — No sorting is applied. The existing order of the categories is unchanged before applying the algorithm. (The existing order of the categories can be seen in the category grouping optional output from bininfo.)

    For more information, see Sort Categories

• For Merge algorithm:

  • {'InitialNumBins',n} — Specifies an integer that determines the number (n >0) of bins that the predictor is initially binned into before merging. Valid for numeric predictors only. Default is 50.

  • {'Measure',MeasureName} — Specifies the measure where 'MeasureName' is one of the following:'Chi2' (default), 'Gini', 'InfoValue', or 'Entropy'.

  • {'MinNumBins',n} — Specifies the minimum number n (n>=2) of bins that result from merging. The default value is 2.

  • {'MaxNumBins',n} — Specifies the maximum number n (n>=2) of bins that result from merging. The default value is 5.

  • {'Tolerance',n} — Specifies the minimum threshold below which merging happens for the information value and entropy statistics. Valid values are in the interval (0.1). Default is 1e3.

  • {'Significance',n} — Significance level threshold for the chi-square statistic, below which merging happens. Values are in the interval [0,1]. Default is 0.9 (90% significance level).

  • {'SortCategories','SortOption'} — Used for categorical predictors only. Used to determine how the predictor categories are sorted as a preprocessing step before applying the algorithm. The values of 'SortOption' are:

    • 'Goods' — The categories are sorted by order of increasing values of “Good.”

    • 'Bads' — The categories are sorted by order of increasing values of “Bad.”

    • 'Odds' — (default) The categories are sorted by order of increasing values of odds, defined as the ratio of “Good” to “Bad” observations, for the given category.

    • 'Totals' — The categories are sorted by order of increasing values of total number of observations (“Good” plus “Bad”).

    • 'None' — No sorting is applied. The existing order of the categories is unchanged before applying the algorithm. (The existing order of the categories can be seen in the category grouping optional output from bininfo.)

    For more information, see Sort Categories

• For EqualFrequency algorithm:

  • {'NumBins',n} — Specifies the desired number (n) of bins. The default is {'NumBins',5} and the number of bins must be a positive number.

  • {'SortCategories','SortOption'} — Used for categorical predictors only. Used to determine how the predictor categories are sorted as a preprocessing step before applying the algorithm. The values of 'SortOption' are:

    • 'Odds' — (default) The categories are sorted by order of increasing values of odds, defined as the ratio of “Good” to “Bad” observations, for the given category.

    • 'Goods' — The categories are sorted by order of increasing values of “Good.”

    • 'Bads' — The categories are sorted by order of increasing values of “Bad.”

    • 'Totals' — The categories are sorted by order of increasing values of total number of observations (“Good” plus “Bad”).

    • 'None' — No sorting is applied. The existing order of the categories is unchanged before applying the algorithm. (The existing order of the categories can be seen in the category grouping optional output from bininfo.)

    For more information, see Sort Categories

• For EqualWidth algorithm:

  • {'NumBins',n} — Specifies the desired number (n) of bins. The default is {'NumBins',5} and the number of bins must be a positive number.

  • {'SortCategories','SortOption'} — Used for categorical predictors only. Used to determine how the predictor categories are sorted as a preprocessing step before applying the algorithm. The values of 'SortOption' are:

    • 'Odds' — (default) The categories are sorted by order of increasing values of odds, defined as the ratio of “Good” to “Bad” observations, for the given category.

    • 'Goods' — The categories are sorted by order of increasing values of “Good.”

    • 'Bads' — The categories are sorted by order of increasing values of “Bad.”

    • 'Totals' — The categories are sorted by order of increasing values of total number of observations (“Good” plus “Bad”).

    • 'None' — No sorting is applied. The existing order of the categories is unchanged before applying the algorithm. (The existing order of the categories can be seen in the category grouping optional output from bininfo.)

    For more information, see Sort Categories

Example: sc = autobinning(sc,'CustAge','Algorithm','Monotone','AlgorithmOptions',{'Trend','Increasing'})

Data Types: cell

Display — Indicator to display information on status of the binning process at command line

'Off' (default) | character vector with values 'On', 'Off'

Indicator to display the information on status of the binning process at command line, specified as the comma-separated pair consisting of 'Display' and a character vector with a value of 'On' or 'Off'.

Data Types: char

Output Arguments

sc — Credit scorecard model

creditscorecard object

Credit scorecard model, returned as an updated creditscorecard object containing the automatically determined binning maps or rules (cut points or category groupings) for one or more predictors. For more information on using the creditscorecard object, see creditscorecard.

Note

If you have previously used the modifybins function to manually modify bins, these changes are lost when running autobinning because all the data is automatically binned based on internal autobinning rules.

More About

Predictor

In the context of a credit scorecard, a predictor a variable or feature used in the credit scoring model to estimate the likelihood of a borrower defaulting on a loan or credit obligation.

Predictors are statistical variables that have been identified as having a significant correlation with credit risk. They are used in predictive modeling to forecast future behavior based on historical data.

Monotone

The 'Monotone' algorithm is an implementation of the Monotone Adjacent Pooling Algorithm (MAPA), also known as Maximum Likelihood Monotone Coarse Classifier (MLMCC); see Anderson or Thomas in the References.

Preprocessing

During the preprocessing phase, preprocessing of numeric predictors consists in applying equal frequency binning, with the number of bins determined by the 'InitialNumBins' parameter (the default is 10 bins). The preprocessing of categorical predictors consists in sorting the categories according to the 'SortCategories' criterion (the default is to sort by odds in increasing order). Sorting is not applied to ordinal predictors. See the Sort Categories definition or the description of AlgorithmOptions option for 'SortCategories' for more information.

Main Algorithm

The following example illustrates how the 'Monotone' algorithm arrives at cut points for numeric data.

Bin	Good	Bad	Iteration1	Iteration2	Iteration3	Iteration4
'[-Inf,33000)'	127	107	0.543
'[33000,38000)'	194	90	0.620	0.683
'[38000,42000)'	135	78	0.624	0.662
'[42000,47000)'	164	66	0.645	0.678	0.713
'[47000,Inf]'	183	56	0.669	0.700	0.740	0.766

Initially, the numeric data is preprocessed with an equal frequency binning. In this example, for simplicity, only the five initial bins are used. The first column indicates the equal frequency bin ranges, and the second and third columns have the “Good” and “Bad” counts per bin. (The number of observations is 1,200, so a perfect equal frequency binning would result in five bins with 240 observations each. In this case, the observations per bin do not match 240 exactly. This is a common situation when the data has repeated values.)

Monotone finds break points based on the cumulative proportion of “Good” observations. In the'Iteration1' column, the first value (0.543) is the number of “Good” observations in the first bin (127), divided by the total number of observations in the bin (127+107). The second value (0.620) is the number of “Good” observations in bins 1 and 2, divided by the total number of observations in bins 1 and 2. And so forth. The first cut point is set where the minimum of this cumulative ratio is found, which is in the first bin in this example. This is the end of iteration 1.

Starting from the second bin (the first bin after the location of the minimum value in the previous iteration), cumulative proportions of “Good” observations are computed again. The second cut point is set where the minimum of this cumulative ratio is found. In this case, it happens to be in bin number 3, therefore bins 2 and 3 are merged.

The algorithm proceeds the same way for two more iterations. In this particular example, in the end it only merges bins 2 and 3. The final binning has four bins with cut points at 33,000, 42,000, and 47,000.

For categorical data, the only difference is that the preprocessing step consists in reordering the categories. Consider the following categorical data:

Bin	Good	Bad	Odds
'Home Owner'	365	177	2.062
'Tenant'	307	167	1.838
'Other'	131	53	2.474

The preprocessing step, by default, sorts the categories by 'Odds'. (See the Sort Categories definition or the description of AlgorithmOptions option for 'SortCategories' for more information.) Then, it applies the same steps described above, shown in the following table:

Bin	Good	Bad	Odds	Iteration1	Iteration2	Iteration3
'Tenant'	307	167	1.838	0.648
'Home Owner'	365	177	2.062	0.661	0.673
'Other'	131	53	2.472	0.669	0.683	0.712

In this case, the Monotone algorithm would not merge any categories. The only difference, compared with the data before the application of the algorithm, is that the categories are now sorted by 'Odds'.

In both the numeric and categorical examples above, the implicit 'Trend' choice is 'Increasing'. (See the description of AlgorithmOptions option for the 'Monotone' 'Trend' option.) If you set the trend to 'Decreasing', the algorithm looks for the maximum (instead of the minimum) cumulative ratios to determine the cut points. In that case, at iteration 1, the maximum would be in the last bin, which would imply that all bins should be merged into a single bin. Binning into a single bin is a total loss of information and has no practical use. Therefore, when the chosen trend leads to a single bin, the Monotone implementation rejects it, and the algorithm returns the bins found after the preprocessing step. This state is the initial equal frequency binning for numeric data and the sorted categories for categorical data. The implementation of the Monotone algorithm by default uses a heuristic to identify the trend ('Auto' option for 'Trend').

Split

Split is a supervised automatic binning algorithm, where a measure is used to split the data into buckets. The supported measures are gini, chi2, infovalue, and entropy.

Internally, the split algorithm proceeds as follows:

1. All categories are merged into a single bin.

2. At the first iteration, all potential cutpoint indices are tested to see which one results in the maximum increase in the information function (Gini, InfoValue, Entropy, or Chi2). That cutpoint is then selected, and the bin is split.

3. The same procedure is reiterated for the next sub-bins.

4. The algorithm stops when the maximum number of bins is reached or when the splitting does not result in any additional change in the information change function.

The following table for a categorical predictor summarizes the values of the change function at each iteration. In this example, 'Gini' is the measure of choice, such that the goal is to see a decrease of the Gini measure at each iteration.

Iteration 0 Bin Number	Member	Gini	Iteration 1 Bin Number	Member	Gini	Iteration 2 Bin Number	Member	Gini
1	'Tenant'		1	'Tenant'		1	'Tenant'	0.45638
1	'Subletter'		1	'Subletter'	0.44789	1	'Subletter'
1	'Home Owner'		1	'Home Owner'		2	'Home Owner'	0.43984
1	'Other'		2	'Other'	0.41015	3	'Other'	0.41015
Total Gini		0.442765			0.442102			0.441822
Relative Change		0			0.001498			0.002128

The relative change at iteration i is with respect to the Gini measure of the entire bins at iteration i-1. The final result corresponds to that from the last iteration which, in this example, is iteration 2.

The following table for a numeric predictor summarizes the values of the change function at each iteration. In this example, 'Gini' is the measure of choice, such that the goal is to see a decrease of the Gini measure at each iteration. Since most numeric predictors in datasets contain many bins, there is a preprocessing step where the data is pre-binned into 50 equal-frequency bins. This makes the pool of valid cutpoints to choose from for splitting smaller and more manageable.

Iteration 0 Bin Number	Member	Gini	Iteration 1 Bin Number	Gini	Iteration 2 Bin Number	Gini	Iteration 3 Bin Number	Gini
1	'21'		'[-Inf,47]'	0.473897	'[-Inf,47]'	0.473897	'[-Inf,35]'	0.494941
1	'22'		'[47,Inf]'	0.385238	'[47,61]'	0.407072	'[35, 47]'	0.463201
1	'23'				'[61,Inf]'	0.208795	'[47, 61]'	0.407072
1	'74'			0			'[61,Inf]'	0.208795
Total Gini		0.442765		0.435035		0.432048		0.430511
Relative Change		0		0.01746		0.006867		0.0356

The resulting split must be such that the information function (content) increases. As such, the best split is the one that results in the maximum information gain. The information functions supported are:

• Gini: Each split results in an increase in the Gini Ratio, defined as:

  G_r = 1- G_hat/G_p

  G_p is the Gini measure of the parent node, that is, of the given bins/categories prior to splitting. G_hat is the weighted Gini measure for the current split:

  G_hat = Sum((nj/N) * Gini(j), j=1..m)

  where

  nj is the total number of observations in the jth bin.

  N is the total number of observations in the dataset.

  m is the number of splits for the given variable.

  Gini(j) is the Gini measure for the jth bin.

  The Gini measure for the split/node j is:

  Gini(j) = 1 - (Gj^2+Bj^2) / (nj)^2

  where Gj, Bj = Number of Goods and Bads for bin j.

• InfoValue: The information value for each split results in an increase in the total information. The split that is retained is the one which results in the maximum gain, within the acceptable gain tolerance. The Information Value (IV) for a given observation j is defined as:

  IV = sum( (pG_i-pB_i) * log(pG_i/pB_i), i=1..n)

  where

  pG_i is the distribution of Goods at observation i, that is Goods(i)/Total_Goods.

  pB_i is the distribution of Bads at observation i, that is Bads(i)/Total_Bads.

  n is the total number of bins.

• Entropy: Each split results in a decrease in entropy variance defined as:

   E = -sum(ni * Ei, i=1..n)  

  where

  ni is the total count for bin i, that is (ni = Gi + Bi).

  Ei is the entropy for row (or bin) i, defined as:

   Ei = -sum(Gi*log2(Gi/ni) + Bi*log2(Bi/ni))/N, 
  i=1..n

• Chi2: Chi2 is computed pairwise for each pair of bins and measures the statistical difference between two groups. Splitting is selected at a point (cutpoint or category indexing) where the maximum Chi2 value is:

   Chi2 = sum(sum((Aij - Eij)^2/Eij , j=1..k), i=m,m+1)

  where

  m takes values from 1 ... n-1, where n is the number of bins.

  k is the number of classes. Here k = 2 for the (Goods, Bads).

  Aij is the number of observations in bin i, jth class.

  Eij is the expected frequency of Aij, which is equal to (Ri*Cj)/N.

  Ri is the number of observations in bin i, which is equal to sum(Aij, j=1..k).

  Cj is the number of observations in the jth class, which is equal to sum(Aij, I = m,m+1).

  N is the total number of observations, which is equal to sum(Cj, j=1..k).

The Chi2 measure for the entire sample (as opposed to the pairwise Chi2 measure for adjacent bins) is:

 Chi2 = sum(sum((Aij - Eij)^2/Eij , j=1..k), i=1..n)

Merge

Merge is a supervised automatic binning algorithm, where a measure is used to merge bins into buckets. The supported measures are chi2, gini, infovalue, and entropy.

Internally, the merge algorithm proceeds as follows:

1. All categories are initially in separate bins.

2. The user selected information function (Chi2, Gini, InfoValue or Entropy) is computed for any pair of adjacent bins.

3. At each iteration, the pair with the smallest information change measured by the selected information function is merged.

4. The merging continues until either:

   1. All pairwise information values are greater than the threshold set by the significance level or the relative change is smaller than the tolerance.

   2. If at the end, the number of bins is still greater than the MaxNumBins allowed, merging is forced until there are at most MaxNumBins bins. Similarly, merging stops when there are only MinNumBins bins.

5. For categorical, original bins/categories are pre-sorted according to the sorting of choice set by the user. For numeric data, the data is preprocessed to get InitialNumBins bins of equal frequency before the merging algorithm starts.

The following table for a categorical predictor summarizes the values of the change function at each iteration. In this example, 'Chi2' is the measure of choice. The default sorting by Odds is applied as a preprocessing step. The Chi2 value reported below at row i is for bins i and i+1. The significance level is 0.9 (90%), so that the inverse Chi2 value is 2.705543. This is the threshold below which adjacent pairs of bins are merged. The minimum number of bins is 2.

Iteration 0 Bin Number	Member	Chi2	Iteration 1 Bin Number	Member	Chi2	Iteration 2 Bin Number	Member	Chi2
1	'Tenant'	1.007613	1	'Tenant'	0.795920	1	'Tenant'
2	'Subletter'	0.257347	2	'Subletter'		1	'Subletter'
3	'Home Owner'	1.566330	2	'Home Owner'	1.522914	1	'Home Owner'	1.797395
4	'Other'		3	'Other'		2	'Other'
Total Chi2		2.573943			2.317717			1.797395

The following table for a numeric predictor summarizes the values of the change function at each iteration. In this example, 'Chi2' is the measure of choice.

Iteration 0 Bin Number	Chi2	Iteration 1 Bins	Chi2		Final Iteration Bins	Chi2
'[-Inf,22]'	0.11814	'[-Inf,22]'	0.11814		'[-Inf,33]'	8.4876
'[22,23]'	1.6464	'[22,23]'	1.6464		'[33, 48]'	7.9369
...		...			'[48,64]'	9.956
'[58,59]'	0.311578	'[58,59]'	0.27489		'[64,65]'	9.6988
'[59,60]'	0.068978	'[59,61]'	1.8403		'[65,Inf]'	NaN
'[60,61]'	1.8709	'[61,62]'	5.7946	...
'[61,62]'	5.7946	...
...		'[69,70]'	6.4271
'[69,70]'	6.4271	'[70,Inf]'	NaN
'[70,Inf]'	NaN
Total Chi2	67.467		67.399			23.198

The resulting merging must be such that any pair of adjacent bins is statistically different from each other, according to the chosen measure. The measures supported for Merge are:

• Chi2: Chi2 is computed pairwise for each pair of bins and measures the statistical difference between two groups. Merging is selected at a point (cutpoint or category indexing) where the maximum Chi2 value is:

   Chi2 = sum(sum((Aij - Eij)^2/Eij , j=1..k), i=m,m+1)

  where

  m takes values from 1 ... n-1, and n is the number of bins.

  k is the number of classes. Here k = 2 for the (Goods, Bads).

  Aij is the number of observations in bin i, jth class.

  Eij is the expected frequency of Aij, which is equal to (Ri*Cj)/N.

  Ri is the number of observations in bin i, which is equal to sum(Aij, j=1..k).

  Cj is the number of observations in the jth class, which is equal to sum(Aij, I = m,m+1).

  N is the total number of observations, which is equal to sum(Cj, j=1..k).

  The Chi2 measure for the entire sample (as opposed to the pairwise Chi2 measure for adjacent bins) is:

   Chi2 = sum(sum((Aij - Eij)^2/Eij , j=1..k), i=1..n)

• Gini: Each merge results in a decrease in the Gini Ratio, defined as:

  G_r = 1- G_hat/G_p

  G_p is the Gini measure of the parent node, that is, of the given bins/categories prior to merging. G_hat is the weighted Gini measure for the current merge:

  G_hat = Sum((nj/N) * Gini(j), j=1..m)

  where

  nj is the total number of observations in the jth bin.

  N is the total number of observations in the dataset.

  m is the number of merges for the given variable.

  Gini(j) is the Gini measure for the jth bin.

  The Gini measure for the merge/node j is:

  Gini(j) = 1 - (Gj^2+Bj^2) / (nj)^2

  where Gj, Bj = Number of Goods and Bads for bin j.

• InfoValue: The information value for each merge will result in a decrease in the total information. The merge that is retained is the one which results in the minimum gain, within the acceptable gain tolerance. The Information Value (IV) for a given observation j is defined as:

  IV = sum( (pG_i-pB_i) * log(pG_i/pB_i), i=1..n)

  where

  pG_i is the distribution of Goods at observation i, that is Goods(i)/Total_Goods.

  pB_i is the distribution of Bads at observation i, that is Bads(i)/Total_Bads.

  n is the total number of bins.

• Entropy: Each merge results in an increase in entropy variance defined as:

   E = -sum(ni * Ei, i=1..n)  

  where

  ni is the total count for bin i, that is (ni = Gi + Bi).

  Ei is the entropy for row (or bin) i, defined as:

   Ei = -sum(Gi*log2(Gi/ni) + Bi*log2(Bi/ni))/N, 
  i=1..n

Note

When using the Merge algorithm, if there are pure bins (bins that have either zero count of Goods or zero count of Bads), the statistics such as Information Value and Entropy have non-finite values. To account for this, a frequency shift of .5 is applied for computing various statistics whenever the algorithm finds pure bins.

Equal Frequency

Unsupervised algorithm that divides the data into a predetermined number of bins that contain approximately the same number of observations.

EqualFrequency is defined as:

Let v[1], v[2],..., v[N] be the sorted list of different values or categories observed in the data. Let f[i] be the frequency of v[i]. Let F[k] = f[1]+...+f[k] be the cumulative sum of frequencies up to the kth sorted value. Then F[N] is the same as the total number of observations.

Define AvgFreq = F[N] / NumBins, which is the ideal average frequency per bin after binning. The nth cut point index is the index k such that the distance abs(F[k] - n*AvgFreq) is minimized.

This rule attempts to match the cumulative frequency up to the nth bin. If a single value contains too many observations, equal frequency bins are not possible, and the above rule yields less than NumBins total bins. In that case, the algorithm determines NumBins bins by breaking up bins, in the order in which the bins were constructed.

The preprocessing of categorical predictors consists in sorting the categories according to the 'SortCategories' criterion (the default is to sort by odds in increasing order). Sorting is not applied to ordinal predictors. See the Sort Categories definition or the description of AlgorithmOptions option for 'SortCategories' for more information.

Equal Width

Unsupervised algorithm that divides the range of values in the domain of the predictor variable into a predetermined number of bins of “equal width.” For numeric data, the width is measured as the distance between bin edges. For categorical data, width is measured as the number of categories within a bin.

The EqualWidth option is defined as:

For numeric data, if MinValue and MaxValue are the minimum and maximum data values, then

Width = (MaxValue - MinValue)/NumBins

and the CutPoints are set to MinValue + Width, MinValue + 2*Width, ... MaxValue – Width. If a MinValue or MaxValue have not been specified using the modifybins function, the EqualWidth option sets MinValue and MaxValue to the minimum and maximum values observed in the data.

For categorical data, if there are NumCats numbers of original categories, then

Width = NumCats / NumBins,

and set cut point indices to the rounded values of Width, 2*Width, ..., NumCats – Width, plus 1.

The preprocessing of categorical predictors consists in sorting the categories according to the 'SortCategories' criterion (the default is to sort by odds in increasing order). Sorting is not applied to ordinal predictors. See the Sort Categories definition or the description of AlgorithmOptions option for 'SortCategories' for more information.

Sort Categories

As a preprocessing step for categorical data, 'Monotone', 'EqualFrequency', and 'EqualWidth' support the 'SortCategories' input. This serves the purpose of reordering the categories before applying the main algorithm. The default sorting criterion is to sort by 'Odds'. For example, suppose that the data originally looks like this:

Bin	Good	Bad	Odds
'Home Owner'	365	177	2.062
'Tenant'	307	167	1.838
'Other'	131	53	2.472

After the preprocessing step, the rows would be sorted by 'Odds' and the table looks like this:

Bin	Good	Bad	Odds
'Tenant'	307	167	1.838
'Home Owner'	365	177	2.062
'Other'	131	53	2.472

The three algorithms only merge adjacent bins, so the initial order of the categories makes a difference for the final binning. The 'None' option for 'SortCategories' would leave the original table unchanged. For a description of the sorting criteria supported, see the description of the AlgorithmOptions option for 'SortCategories'.

Upon the construction of a scorecard, the initial order of the categories, before any algorithm or any binning modifications are applied, is the order shown in the first output of bininfo. If the bins have been modified (either manually with modifybins or automatically with autobinning), use the optional output (cg,'category grouping') from bininfo to get the current order of the categories.

The 'SortCategories' option has no effect on categorical predictors for which the 'Ordinal' parameter is set to true (see the 'Ordinal' input parameter in MATLAB^® categorical arrays for categorical. Ordinal data has a natural order, which is honored in the preprocessing step of the algorithms by leaving the order of the categories unchanged. Only categorical predictors whose 'Ordinal' parameter is false (default option) are subject to reordering of categories according to the 'SortCategories' criterion.

Using autobinning with Weights

When observation weights are defined using the optional WeightsVar argument when creating a creditscorecard object, instead of counting the rows that are good or bad in each bin, the autobinning function accumulates the weight of the rows that are good or bad in each bin.

The “frequencies” reported are no longer the basic “count” of rows, but the “cumulative weight” of the rows that are good or bad and fall in a particular bin. Once these “weighted frequencies” are known, all other relevant statistics (Good, Bad, Odds, WOE, and InfoValue) are computed with the usual formulas. For more information, see Credit Scorecard Modeling Using Observation Weights.

References

[1] Anderson, R. The Credit Scoring Toolkit. Oxford University Press, 2007.

[2] Kerber, R. "ChiMerge: Discretization of Numeric Attributes." AAAI-92 Proceedings. 1992.

[3] Liu, H., et. al. Data Mining, Knowledge, and Discovery. Vol 6. Issue 4. October 2002, pp. 393-423.

[4] Refaat, M. Data Preparation for Data Mining Using SAS. Morgan Kaufmann, 2006.

[5] Refaat, M. Credit Risk Scorecards: Development and Implementation Using SAS. lulu.com, 2011.

[6] Thomas, L., et al. Credit Scoring and Its Applications. Society for Industrial and Applied Mathematics, 2002.

Version History

Introduced in R2014b