フーリエニューラル演算子を使用した PDE の求解

この例では、偏微分方程式 (PDE) の解を出力するフーリエニューラル演算子 (FNO) ニューラルネットワークに学習させる方法を示します。

"ニューラル演算子" [1] は、関数空間の間をマッピングするニューラルネットワークの一種です。たとえば、システムの初期条件が与えられたときに PDE の解を出力するように学習できます。"フーリエニューラル演算子" (FNO) [2] は、フーリエ変換を活用することで、これらのマッピングをより効率的に学習できるニューラル演算子です。具体的には、空間領域における入力関数 $f$ に対して、ニューラルネットワークの層は、 $F (f) = f_{}^{ˆ}$ となる変換 $F$ を学習します。ここで $f_{}^{ˆ}$ は $f$ のフーリエ変換です。これにより、FNO は周波数領域で動作できるようになります。ニューラルネットワークを使用して PDE の解を予測すると、数値的な計算よりも高速に解を得られる場合があります。

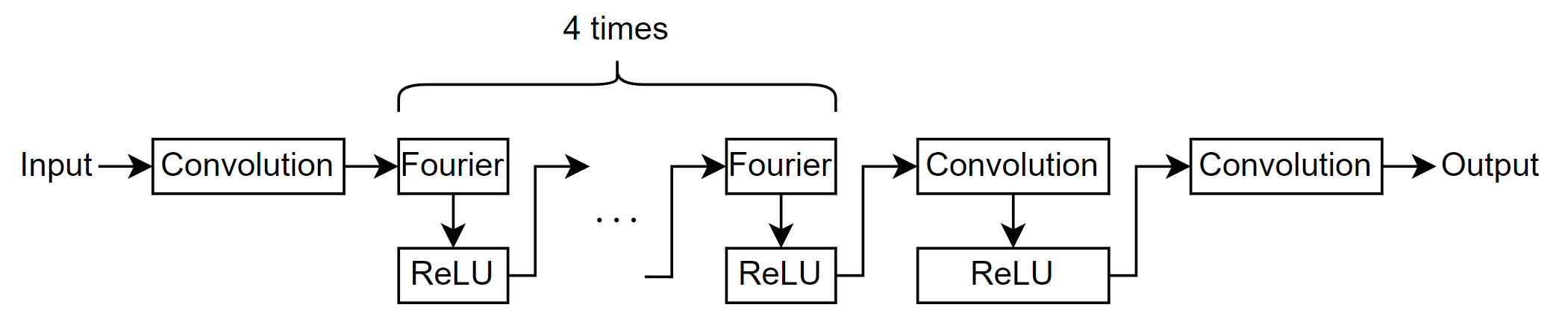
次の図は、FNO を通るデータの流れを示しています。

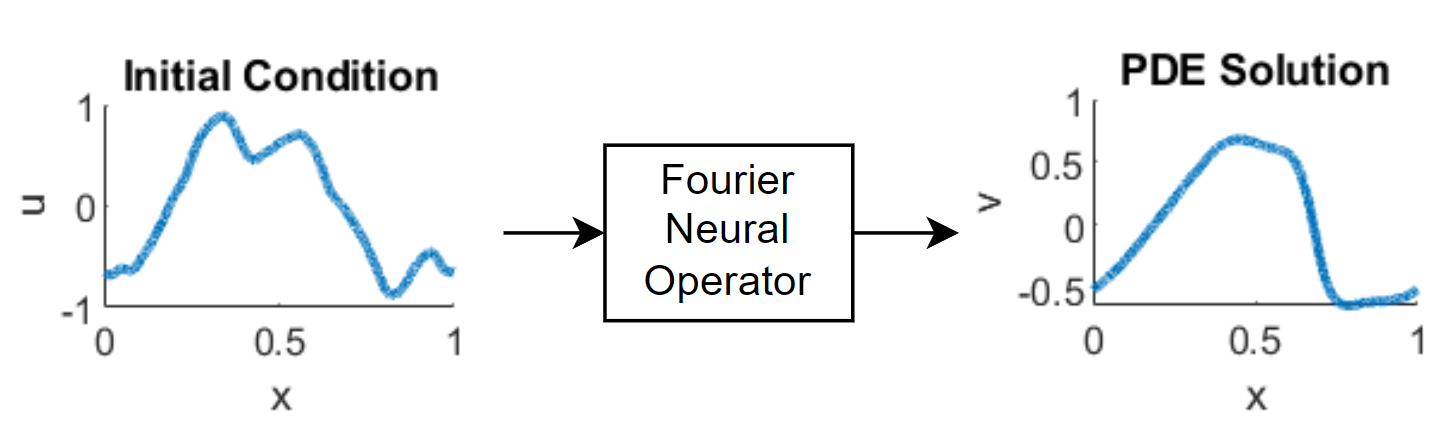
Diagram of data flowing through FNO. The input is a function labeled "Initial Condition". The output is a function labeled "PDE Solution".

FNO は関数空間の間のマッピングを学習するため、学習データの解像度よりも高い解像度で出力関数を評価できます。この機能はゼロショット超解像 (ZSSR) として知られています。つまり、ZSSR は、追加の高解像度の例を必要とせずに、入力データと出力データの解像度を元の学習データを超えて向上させる機能です。次の図は、予測のための低解像度の学習データと高解像度の入力、およびそれらの出力の違いを示しています。

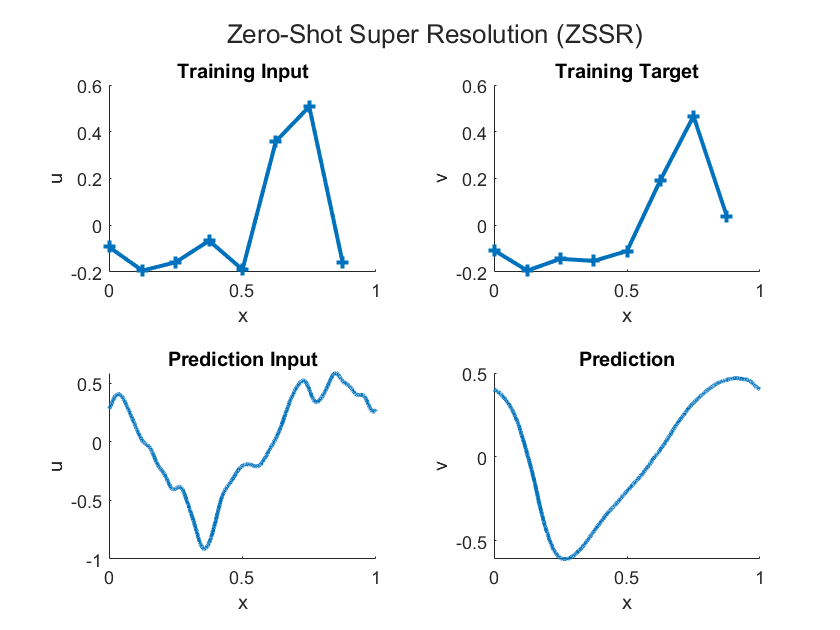
Plots showing low resolution and high resolution inputs and outputs. The low-resolution functions are composed of a small number of straight lines between points. The high-resolution functions are smooth curves.

この例では、1 次元バーガーズ方程式の解を出力するように FNO に学習させます。

学習データの読み込み

1 次元バーガーズ方程式のデータを読み込みます。

バーガーズ方程式は、流体力学、非線形音響学、気体力学、交通流など、応用数学のさまざまな分野で用いられる PDE です。その PDE は次のようなものです。

$\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = \frac{1}{R e} \frac{\partial^{2} u}{\partial x^{2}}, x \in (0, 1), t \in (0, 1),$

ここで、 $R e$ はレイノルズ数です。初期条件は次のとおりです。

$u (x, 0) = u_{0} (x), x \in (0, 1)$

この方程式は、空間領域全体にわたって周期的境界条件を課し、初期条件 $u_{0}$ から時刻 $t = 1 : u_{0} ⟼ u (x, 1)$ における解を示しています。

1 次元バーガーズ方程式のデータを burgers_data_R10.mat から読み込みます。このデータには、バーガーズ方程式の初期速度 $u_{0}$ と解 $u (x, 1)$ が含まれています。

dataFile = "burgers_data_R10.mat";
if ~exist(dataFile,"file")
    location = "https://ssd.mathworks.com/supportfiles/nnet/data/burgers1d/burgers_data_R10.mat";
    websave(dataFile,location); 
end

data = load(dataFile,"a","u");
u0 = data.a;
u1 = data.u;

学習データをいくつか表示します。

numPlots = 3;
gridSize = size(u0,2);
figure
tiledlayout(numPlots,2)
for i = 1:numPlots
    nexttile
    plot(linspace(0,1,gridSize),u0(i,:));
    title("Observation " + i + newline + "Initial Condition")
    xlabel("x")
    ylabel("u")

    nexttile
    plot(linspace(0,1,gridSize),u1(i,:));
    title("PDE Solution")
    xlabel("x")
    ylabel("v")
end

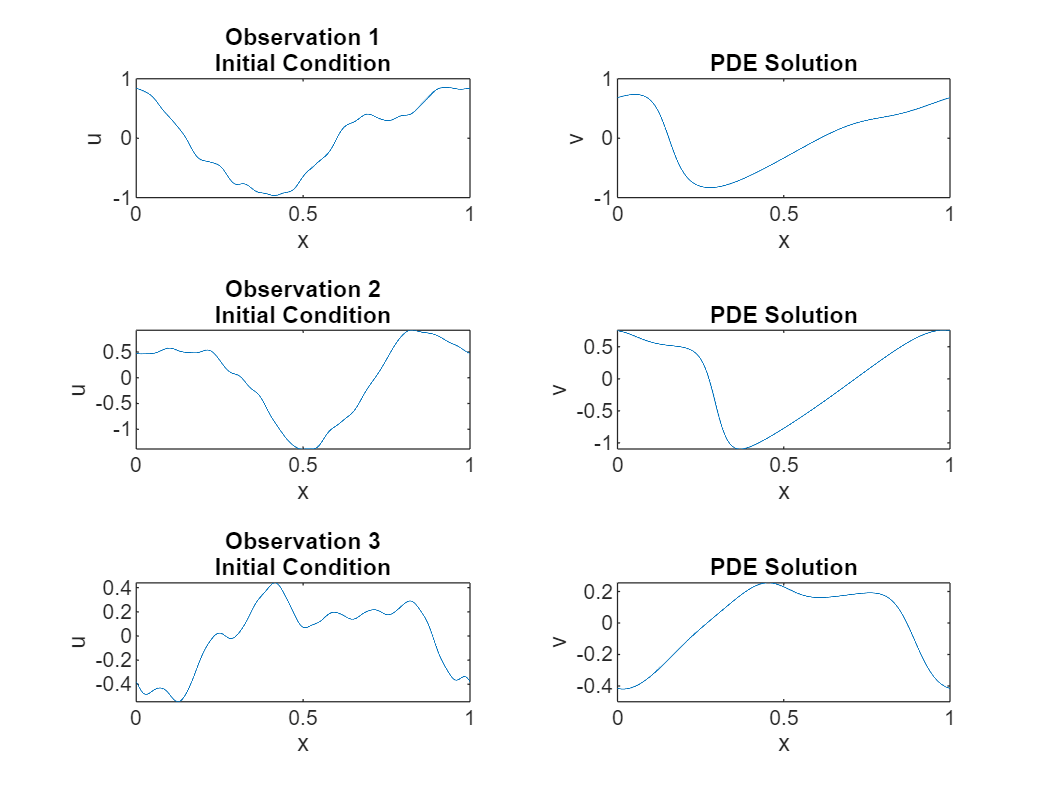
学習データの準備

この例にサポートファイルとして添付されている trainingPartitions 関数を使用して、学習データとテストデータを分割します。この関数にアクセスするには、例をライブスクリプトとして開きます。データの 80% は学習に使用し、10% は検証に使用し、残りの 10% はテストに使用します。

numObservations = size(u0,1);
[idxTrain,idxValidation,idxTest] = trainingPartitions(numObservations,[0.8 0.1 0.1]);
U0Train = u0(idxTrain,:);
U1Train = u1(idxTrain,:);

U0Validation = u0(idxValidation,:);
U1Validation = u1(idxValidation,:);
U0Test = u0(idxTest,:);

FNO での処理量を減らすには、学習データと検証データをダウンサンプリングして、グリッドサイズが 1024 になるようにします。

gridSizeDownsampled = 1024;
downsampleFactor = floor(gridSize./gridSizeDownsampled);

U0Train = U0Train(:,1:downsampleFactor:end);
U1Train = U1Train(:,1:downsampleFactor:end);
U0Validation = U0Validation(:,1:downsampleFactor:end);
U1Validation = U1Validation(:,1:downsampleFactor:end);

FNO は、空間座標 (グリッド) に対応するチャネルをもつ入力データを必要とします。グリッドを作成し、入力データと連結します。

xMin = 0;
xMax = 1;
xGrid = linspace(xMin,xMax,gridSizeDownsampled);

xGridTrain = repmat(xGrid, [numel(idxTrain) 1]);
xGridValidation = repmat(xGrid, [numel(idxValidation) 1]);

U0Train = cat(3,U0Train,xGridTrain);
U0Validation = cat(3,U0Validation,xGridValidation);

学習セットと検証セットのサイズを表示します。1 番目、2 番目、および 3 番目の次元は、それぞれバッチ次元、空間次元、チャネル次元です。

size(U0Train)

ans = 1×3

        1638        1024           2

size(U0Validation)

ans = 1×3

         204        1024           2

ニューラルネットワークアーキテクチャの定義

ニューラルネットワークアーキテクチャを定義します。ネットワークは複数のフーリエ層と畳み込み層で構成されています。

フーリエ層の定義

周波数領域で動作するネットワーク層を作成する関数を定義します。

この層は、入力に畳み込みとスペクトル畳み込みを適用して処理し、それらの出力を合計します。次の図はこの層のアーキテクチャを示しています。

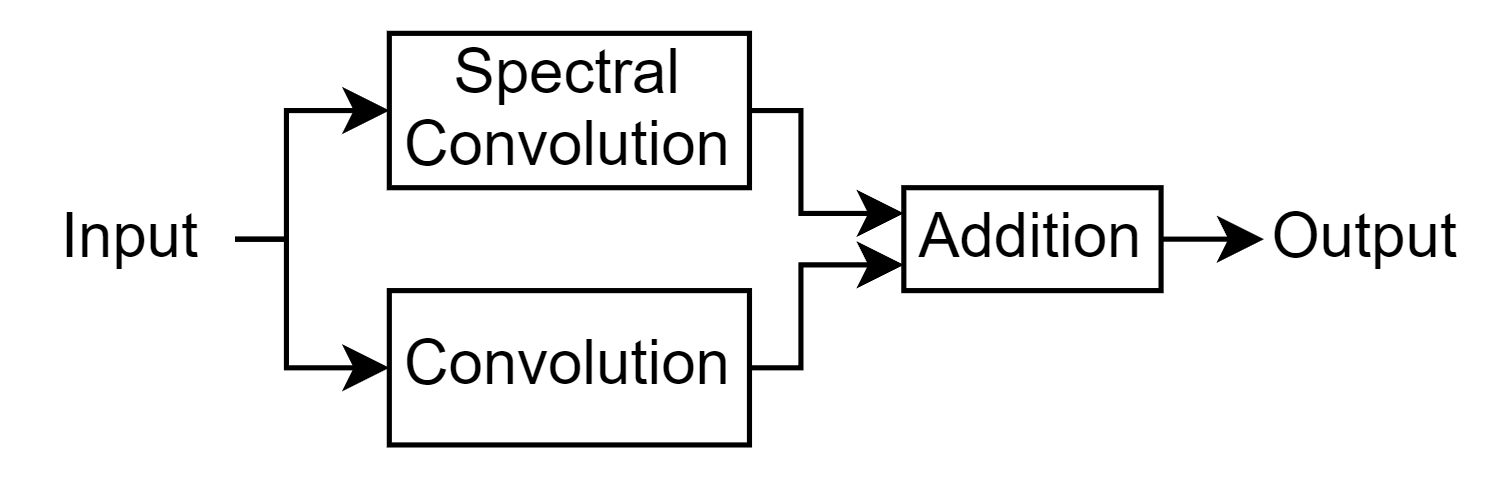
Diagram showing FNO layer architecture. The input is connected to both a spectral convolution layer and a convolution layer. The outputs of the two convolution layers are connected to an addition layer. The output of the FNO layer is the output of the addition layer.

スペクトル畳み込み層は周波数領域で畳み込みを適用するもので、ネットワークが複雑な空間依存性を学習できるため、PDE の求解に特に有用です。フーリエ層は、スペクトル畳み込み演算を適用するために、この例にサポートファイルとして添付されているカスタム層 spectralConvolution1dLayer を使用します。この層にアクセスするには、この例をライブスクリプトとして開きます。

function layer = fourierLayer(spatialWidth,numModes,args)

arguments
    spatialWidth
    numModes
    args.Name = ""
end
name = args.Name;

net = dlnetwork;

layers = [
    identityLayer(Name="in")
    spectralConvolution1dLayer(spatialWidth,numModes,Name="specConv")
    additionLayer(2,Name="add")];

net = addLayers(net,layers);

layer = convolution1dLayer(1,spatialWidth,Name="fc");
net = addLayers(net,layer);

net = connectLayers(net,"in","fc");
net = connectLayers(net,"fc","add/in2");

layer = networkLayer(net,Name=name);

end

ニューラルネットワークの作成

ニューラルネットワークアーキテクチャを定義します。この例のネットワークは、直列に接続された複数の Fourier-ReLU ブロックで構成されています。

Diagram of the neural network of layers connected in series. From left to right, there is the input, convolution, four fourier-ReLU blocks, convolution, ReLU, convolution, and output.

次のオプションを指定します。

フーリエ層には、空間の幅が 16 である 16 モードを指定します。
サイズ [NaN spatialWidth 2]、形式 "BSC" (バッチ、空間、チャネル) の入力層を使用します。ここで、spatialWidth はフーリエ層の空間の幅です。
convolution-ReLU ブロックには、128 個の 1 行 1 列のフィルターを指定します。
最後の畳み込み層には、1 行 1 列のフィルターを 1 つ指定します。

numModes = 16;
spatialWidth = 64; 

layers = [
    inputLayer([NaN spatialWidth 2],"BSC");
    convolution1dLayer(1,spatialWidth,Name="fc0")
    fourierLayer(spatialWidth,numModes,Name="fourier1");
    reluLayer
    fourierLayer(spatialWidth,numModes,Name="fourier2")
    reluLayer
    fourierLayer(spatialWidth,numModes,Name="fourier3")
    reluLayer
    fourierLayer(spatialWidth,numModes,Name="fourier4")
    reluLayer
    convolution1dLayer(1,128)
    reluLayer
    convolution1dLayer(1,1)];

学習オプション

学習オプションを指定します。オプションの中から選択するには、経験的解析が必要です。実験を実行してさまざまな学習オプションの構成を調べるには、実験マネージャーアプリを使用できます。

SGDM ソルバーを使用して学習させます。
初期学習率 0.001、低下係数 0.5 の区分的学習率スケジュールを使用して学習させます。
ミニバッチサイズを 20 として 30 エポック学習させます。
すべてのエポックでデータをシャッフルします。
入力データにはバッチ次元、空間次元、チャネル次元に対応する次元があるため、入力データ形式を "BSC" として指定します。
学習の進行状況をプロットで監視し、検証データを指定します。
詳細出力を無効にします。

schedule = piecewiseLearnRate(DropFactor=0.5);

options = trainingOptions("sgdm", ...
    InitialLearnRate=1e-3, ...
    LearnRateSchedule=schedule, ...
    MaxEpochs=30, ...
    MiniBatchSize=20, ...
    Shuffle="every-epoch", ...
    InputDataFormats="BSC", ...
    Plots="training-progress", ...
    ValidationData={U0Validation,U1Validation}, ...
    Verbose=false);

相対 $L_{2}$ 損失関数の定義

予測とターゲットを入力として受け取り、相対的な $L_{2}$ 損失を返す relativeL2Loss 関数を作成します。相対 $L_{2}$ 損失関数は、予測値とターゲットの差のユークリッドノルムを使用してスケールを考慮し、それをターゲットのユークリッドノルムで割る $L_{2}$ 損失関数のバリエーションです。

$R e l a t i v e L 2 (Y, T) = \sum_{n = 1}^{N} \frac{‖ T_{n} - Y_{n} ‖_{2}}{‖ T_{n} ‖_{2}}$

ここで、

$Y$ は予測を表します。
$T$ はターゲットを表します。
$N$ は観測数を表します。

function loss = relativeL2Loss(Y,T)

Y = stripdims(Y,"BSC");
T = stripdims(T,"BSC");

p = vecnorm(T-Y,2,2);
q = vecnorm(T,2,2);

loss = sum(p./q, 1);

end

ネットワークの学習

関数trainnetを使用してニューラルネットワークに学習させます。カスタム損失関数 relativeL2Loss を使用します。既定では、関数 trainnet は利用可能な GPU がある場合にそれを使用します。GPU を使用するには、Parallel Computing Toolbox™ ライセンスとサポートされている GPU デバイスが必要です。サポートされているデバイスの詳細については、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。そうでない場合、関数は CPU を使用します。実行環境を手動で選択するには、ExecutionEnvironment 学習オプションを使用します。

net = trainnet(U0Train,U1Train,layers,@relativeL2Loss,options);

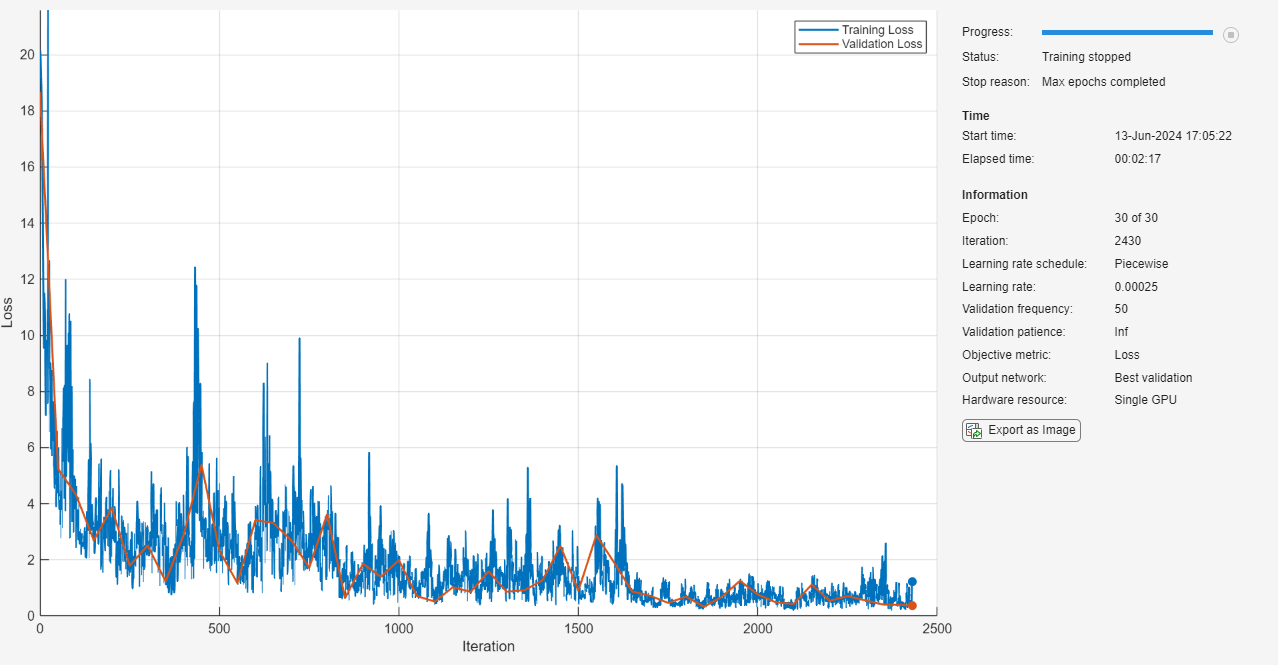
ネットワークのテスト

真のラベルをもつホールドアウトされたテストセットの予測を比較して、その平方根平均二乗誤差 (RMSE) を計算することで、モデルの予測パフォーマンスをテストします。

学習データの場合と同じ手順を使い、テストデータをダウンサンプリングして、グリッドを連結します。

xGridTest = repmat(xGrid, [numel(idxTest) 1]);

U0Test = U0Test(:,1:downsampleFactor:end);
U0Test = cat(3,U0Test,xGridTest);

U1Test = u1(idxTest,:);
U1Test = U1Test(:,1:downsampleFactor:end);

testnet関数を使用してニューラルネットワークをテストします。既定では、testnet 関数は利用可能な GPU がある場合にそれを使用します。そうでない場合、関数は CPU を使用します。実行環境を手動で選択するには、testnet 関数の ExecutionEnvironment 引数を使用します。

rmseTest = testnet(net,U0Test,U1Test,"rmse")

rmseTest = 
0.0112

ZSSR の精度を評価するには、ダウンサンプリングせずにテストデータを使用してネットワークをテストします。

xGridZSSR = linspace(xMin,xMax,gridSize);
xGridTestZSSR = repmat(xGridZSSR, [numel(idxTest) 1]);

U0TestZSSR = u0(idxTest,:);
U0TestZSSR = cat(3,U0TestZSSR,xGridTestZSSR);
U1TestZSSR = u1(idxTest,:);

rmseTestZSSR = testnet(net,U0TestZSSR,U1TestZSSR,"rmse")

rmseTestZSSR = 
0.0113

新しいデータでの予測の実行

ニューラルネットワークを使用して予測を行います。

新しいデータを読み込みます。例として、最初の 3 つのテスト観測値を使用します。

dataNew = u0(idxTest(1:3),:);
numObservationsNew = size(dataNew,1);

グリッドサイズを計算し、それをデータと連結します。

gridSizeNew = size(dataNew,2);
xGridNew = linspace(xMin,xMax,gridSizeNew);
xGridNew = repmat(xGridNew, [size(dataNew,1) 1]);
U0New = cat(3,dataNew,xGridNew);

関数minibatchpredictを使用して予測を行います。既定では、関数 minibatchpredict は利用可能な GPU がある場合にそれを使用します。そうでない場合、関数は CPU を使用します。実行環境を手動で選択するには、ExecutionEnvironment オプションを使用します。

Y = minibatchpredict(net,U0New);

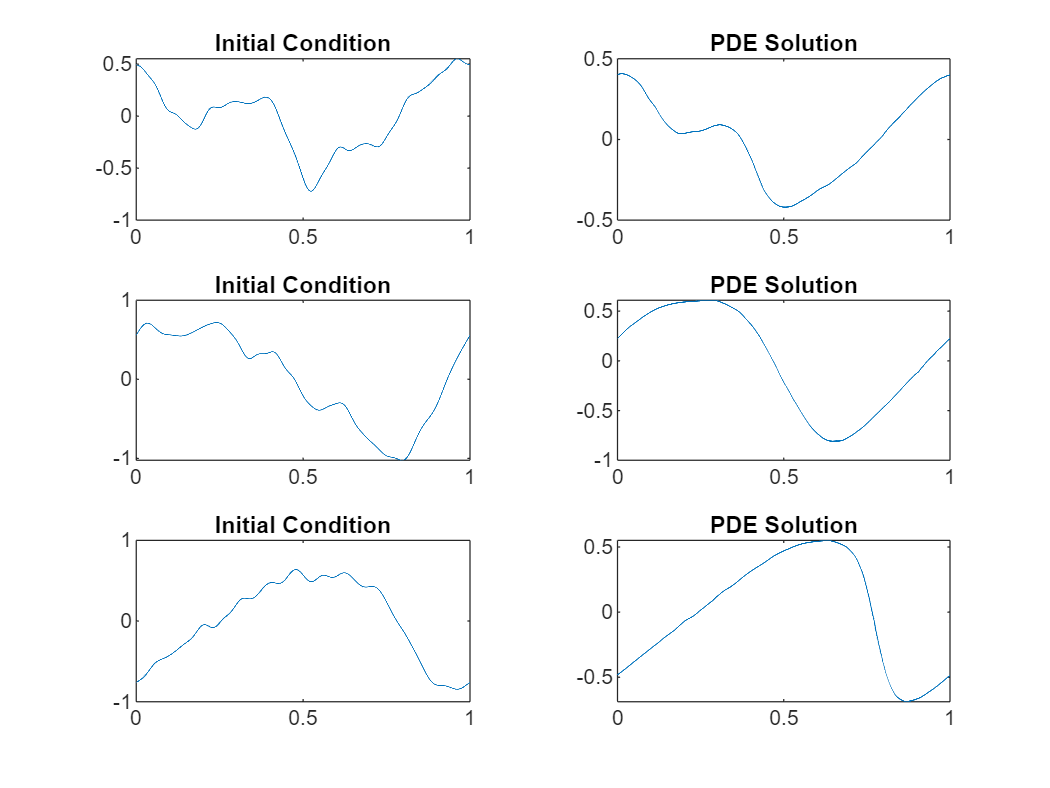
プロットで予測を可視化します。

figure
tiledlayout("flow")
for i = 1:numObservationsNew
    nexttile
    plot(xGridNew(i,:),dataNew(i,:))
    title("Initial Condition")

    nexttile
    plot(xGridNew(i,:),Y(i,:))
    title("PDE Solution")
end

参考文献

Li, Zongyi, Nikola Kovachki, Kamyar Azizzadenesheli, Burigede Liu, Kaushik Bhattacharya, Andrew Stuart, and Anima Anandkumar. “Neural Operator: Graph Kernel Network for Partial Differential Equations.” arXiv, March 6, 2020. http://arxiv.org/abs/2003.03485.
Li, Zongyi, Nikola Kovachki, Kamyar Azizzadenesheli, Burigede Liu, Kaushik Bhattacharya, Andrew Stuart, and Anima Anandkumar. “Fourier Neural Operator for Parametric Partial Differential Equations,” 2020. https://openreview.net/forum?id=c8P9NQVtmnO.

参考

trainingOptions | trainnet | dlnetwork

フーリエ ニューラル演算子を使用した PDE の求解