Physics Informed Neural Network を使用した ODE の求解

この例では、Physics Informed Neural Network (PINN) に学習させて常微分方程式 (ODE) の解を予測する方法を示します。

すべての微分方程式に閉形式解があるとは限りません。この種の方程式の近似解を求める従来式の数値アルゴリズムは数多くあります。Physics Informed Neural Network (PINN) [1] は、構造と学習プロセスに物理法則を組み込んだニューラルネットワークです。物理システムを定義する ODE の解を出力するニューラルネットワークに学習させることができます。このアプローチには、閉じた解析形式で微分可能近似解を得られるなど、いくつかの利点があります [2]。

この例では、以下を行う方法を説明します。

$x \in [0, 2]$ の範囲での学習データの生成。
$x$ を入力として受け取り、ODE $\dot{y} = - 2 xy$ を $x$ について解いた近似解を出力として返すニューラルネットワークの定義。
カスタム損失関数でのネットワークの学習。
ネットワーク予測と解析解の比較。

ODE と損失関数

この例では、ODE

$\dot{y} = - 2 xy,$

を、初期条件 $y (0) = 1$ で解きます。この ODE には以下の解析解があります。

$y (x) = e^{- x^{2}} .$

ODE と初期状態を満たさず逸脱することにペナルティを課す、カスタム損失関数を定義します。この例では、損失関数は ODE 損失と初期条件損失の重み付き和であり、以下のようになります。

$L_{θ} (x) = ‖ {y_{}^{˙}}_{θ} + 2 x y_{θ} ‖^{2} + k ‖ y_{θ} (0) - 1 ‖^{2}$

$θ$ はネットワークパラメーター、 $k$ は定数係数、 $y_{θ}$ はネットワークによって予測された解、 $\dot{y_{θ}}$ は自動微分を使用して計算された予測解の導関数です。項 $‖ \dot{y_{θ}} + 2 {xy}_{θ} ‖^{2}$ は ODE 損失であり、予測解が ODE の定義を満たすことからどれだけ逸脱するかを定量化します。項 $‖ y_{θ} (0) - 1 ‖^{2}$ は初期条件損失であり、予測解が初期条件を満たすことからどれだけ逸脱するかを定量化します。

入力データの生成とネットワークの定義

範囲 $x \in [0, 2]$ に 10,000 個の学習データ点を生成します。

x = linspace(0,2,10000)';

ODE を解くためのネットワークを定義します。入力は実数 $x \in R$ であるため、入力サイズを 1 に指定します。

inputSize = 1;
layers = [
    featureInputLayer(inputSize,Normalization="none")
    fullyConnectedLayer(10)
    sigmoidLayer
    fullyConnectedLayer(1)
    sigmoidLayer];

層配列から dlnetwork オブジェクトを作成します。

net = dlnetwork(layers)

net = 
  dlnetwork with properties:

         Layers: [5×1 nnet.cnn.layer.Layer]
    Connections: [4×2 table]
     Learnables: [4×3 table]
          State: [0×3 table]
     InputNames: {'input'}
    OutputNames: {'layer_2'}
    Initialized: 1

  View summary with summary.

モデル損失関数の定義

この例のモデル損失関数のセクションにリストされている関数 modelLoss を作成します。この関数は、ニューラルネットワーク、入力データのミニバッチ、および初期条件損失に関連付けられた係数を入力として受け取ります。この関数は、損失およびニューラルネットワークの学習可能なパラメーターに関する損失の勾配を返します。

学習オプションの指定

ミニバッチサイズを 100 として 15 エポック学習させます。

numEpochs = 15;
miniBatchSize = 100;

SGDM 最適化のオプションを指定します。学習率に 0.5、学習率低下係数に 0.5、学習率低下周期に 5、モーメンタムに 0.9 を指定します。

initialLearnRate = 0.5;
learnRateDropFactor = 0.5;
learnRateDropPeriod = 5;
momentum = 0.9;

損失関数の初期条件項の係数を 7 に指定します。この係数は、損失に対する初期条件の相対的寄与を指定します。このパラメーターを調整すると、学習の収束が速くなります。

icCoeff = 7;

モデルの学習

学習中にデータのミニバッチを使用するには、次のようにします。

学習データから arrayDatastore オブジェクトを作成。
minibatchqueueオブジェクトを作成して、arrayDatastore オブジェクトを入力として受け取り、ミニバッチサイズを指定し、部分的なミニバッチを破棄し、学習データの形式が "BC" (バッチ、チャネル) となるようにします。

既定では、minibatchqueue オブジェクトは、基となる型が single の dlarray オブジェクトにデータを変換します。また、GPU が使用可能な場合は、各出力を gpuArray に変換します。GPU を使用するには、Parallel Computing Toolbox™ とサポートされている GPU デバイスが必要です。サポートされているデバイスの詳細については、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。

ads = arrayDatastore(x,IterationDimension=1);
mbq = minibatchqueue(ads, ...
    MiniBatchSize=miniBatchSize, ...
    PartialMiniBatch="discard", ...
    MiniBatchFormat="BC");

SGDM ソルバーの速度パラメーターを初期化します。

velocity = [];

学習の進行状況モニター用に合計反復回数を計算します。

numObservationsTrain = numel(x);
numIterationsPerEpoch = floor(numObservationsTrain / miniBatchSize);
numIterations = numEpochs * numIterationsPerEpoch;

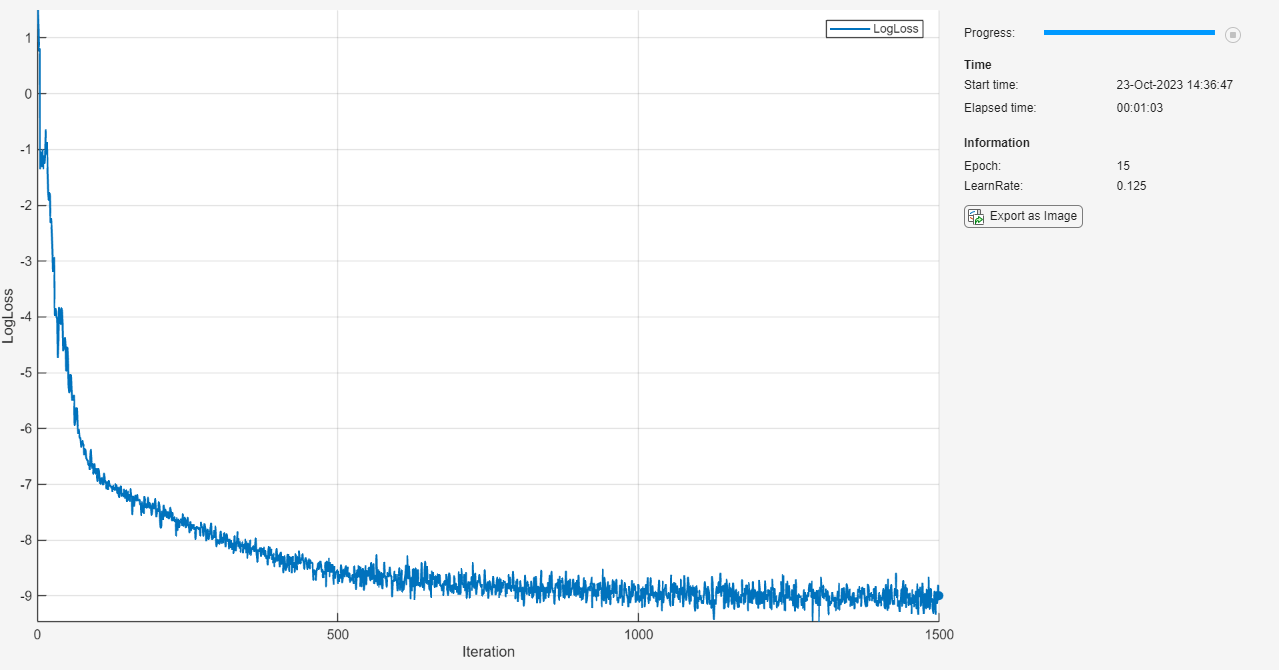
TrainingProgressMonitor オブジェクトを初期化します。監視オブジェクトを作成するとタイマーが開始されるため、学習ループに近いところでオブジェクトを作成するようにしてください。

monitor = trainingProgressMonitor( ...
    Metrics="LogLoss", ...
    Info=["Epoch" "LearnRate"], ...
    XLabel="Iteration");

カスタム学習ループを使用してネットワークに学習させます。各エポックについて、データをシャッフルしてデータのミニバッチをループで回します。各ミニバッチで次を行います。

関数 dlfeval および modelLoss を使用してモデルの損失と勾配を評価します。
関数 sgdmupdate を使用してネットワークパラメーターを更新します。
学習の進行状況を表示します。
Stop プロパティが true の場合は停止します。[停止] ボタンをクリックすると、TrainingProgressMonitor オブジェクトの Stop プロパティ値が true に変わります。

learnRateDropPeriod エポックごとに、学習率に learnRateDropFactor を乗算します。

epoch = 0;
iteration = 0;
learnRate = initialLearnRate;
start = tic;

% Loop over epochs.
while epoch < numEpochs  && ~monitor.Stop
    epoch = epoch + 1;

    % Shuffle data.
    mbq.shuffle

    % Loop over mini-batches.
    while hasdata(mbq) && ~monitor.Stop

        iteration = iteration + 1;

        % Read mini-batch of data.
        X = next(mbq);

        % Evaluate the model gradients and loss using dlfeval and the modelLoss function.
        [loss,gradients] = dlfeval(@modelLoss, net, X, icCoeff);

        % Update network parameters using the SGDM optimizer.
        [net,velocity] = sgdmupdate(net,gradients,velocity,learnRate,momentum);

        % Update the training progress monitor.
        recordMetrics(monitor,iteration,LogLoss=log(loss));
        updateInfo(monitor,Epoch=epoch,LearnRate=learnRate);
        monitor.Progress = 100 * iteration/numIterations;

    end
    
    % Reduce the learning rate.
    if mod(epoch,learnRateDropPeriod)==0
        learnRate = learnRate*learnRateDropFactor;
    end
end

モデルのテスト

予測と解析解を比較して、ネットワークの精度をテストします。

範囲 $x \in [0, 4]$ でテストデータを生成して、ネットワークが学習範囲 $x \in [0, 2]$ の外に外挿できるかどうかを確認します。

xTest = linspace(0,4,1000)';

関数minibatchpredictを使用して予測を行います。既定では、関数 minibatchpredict は利用可能な GPU がある場合にそれを使用します。GPU を使用するには、Parallel Computing Toolbox™ ライセンスとサポートされている GPU デバイスが必要です。サポートされているデバイスの詳細については、GPU 計算の要件 (Parallel Computing Toolbox)を参照してください。そうでない場合、関数は CPU を使用します。実行環境を指定するには、ExecutionEnvironment オプションを使用します。

yModel = minibatchpredict(net,xTest);

解析解を求めます。

yAnalytic = exp(-xTest.^2);

解析解とモデル予測を対数スケールでプロットして比較します。

figure;
plot(xTest,yAnalytic,"-")
hold on
plot(xTest,yModel,"--")
legend("Analytic","Model")
xlabel("x")
ylabel("y (log scale)")
set(gca,YScale="log")

モデルは、学習範囲 $x \in [0, 2]$ で解析解を正確に近似し、範囲 $x \in (2, 4]$ ではより低い精度で外挿します。

学習範囲 $x \in [0, 2]$ で平均二乗相対誤差を計算します。

yModelTrain = yModel(1:500);
yAnalyticTrain = yAnalytic(1:500);

errorTrain = mean(((yModelTrain-yAnalyticTrain)./yAnalyticTrain).^2)

errorTrain = single

0.0029

外挿範囲 $x \in (2, 4]$ で平均二乗相対誤差を計算します。

yModelExtra = yModel(501:1000);
yAnalyticExtra = yAnalytic(501:1000);

errorExtra = mean(((yModelExtra-yAnalyticExtra)./yAnalyticExtra).^2)

errorExtra = single

6.9634e+05

平均二乗相対誤差が、学習範囲よりも外挿範囲において高くなっていることに注意してください。

モデル損失関数

関数 modelLoss は、dlnetwork オブジェクト net、入力データ X のミニバッチ、および初期条件損失に関連付けられた係数 icCoeff を入力として受け取ります。この関数は、net の学習可能なパラメーターに関する損失の勾配と対応する損失を返します。損失は、ODE 損失と初期条件損失の重み付き和として定義されます。この損失の評価には、2 階微分が必要です。2 階自動微分を有効にするには、関数 dlgradient を使用して、EnableHigherDerivatives の名前と値の引数を true に設定します。

function [loss,gradients] = modelLoss(net, X, icCoeff)
y = forward(net,X);

% Evaluate the gradient of y with respect to x. 
% Since another derivative will be taken, set EnableHigherDerivatives to true.
dy = dlgradient(sum(y,"all"),X,EnableHigherDerivatives=true);

% Define ODE loss.
eq = dy + 2*y.*X;

% Define initial condition loss.
ic = forward(net,dlarray(0,"CB")) - 1;

% Specify the loss as a weighted sum of the ODE loss and the initial condition loss.
loss = mean(eq.^2,"all") + icCoeff * ic.^2;

% Evaluate model gradients.
gradients = dlgradient(loss, net.Learnables);

end

参考文献

Maziar Raissi, Paris Perdikaris, and George Em Karniadakis, Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations https://arxiv.org/abs/1711.10561
Lagaris, I. E., A. Likas, and D. I. Fotiadis. “Artificial Neural Networks for Solving Ordinary and Partial Differential Equations.” IEEE Transactions on Neural Networks 9, no. 5 (September 1998): 987–1000. https://doi.org/10.1109/72.712178.

参考

dlarray | dlfeval | dlgradient