動的ニューラルネットワークのしくみ

フィードフォワードおよび再帰型ニューラルネットワーク

動的ネットワークは、フィードフォワード結合のみを含むものとフィードバック、つまり再帰結合を含むものの 2 つのカテゴリに分けることができます。静的ネットワーク、フィードフォワード動的ネットワーク、および再帰型動的ネットワークの違いを理解するため、いくつかのネットワークを作成し、入力シーケンスに対してそれらがどのように応答するかを確認します (必要に応じて、最初に動的ネットワークでの逐次入力によるシミュレーションを再度確認してください)。

次のコマンドは、パルス入力シーケンスを作成してプロットします。

p = {0 0 1 1 1 1 0 0 0 0 0 0};
stem(cell2mat(p))

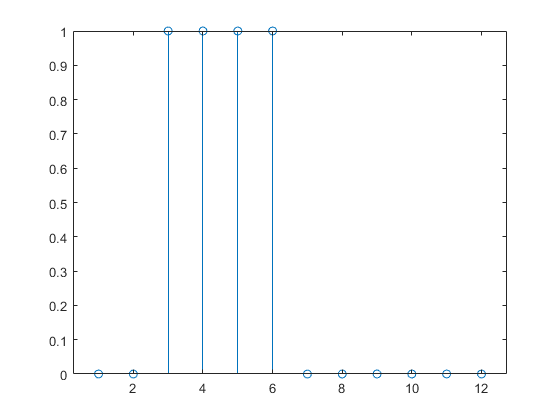
静的ネットワークを作成し、パルスシーケンスに対するネットワーク応答を確認します。次のコマンドは、1 つの層と 1 つのニューロンを持ち、バイアスがなく、重みが 2 のシンプルな線形ネットワークを作成します。

net = linearlayer;
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = 2;

view(net)

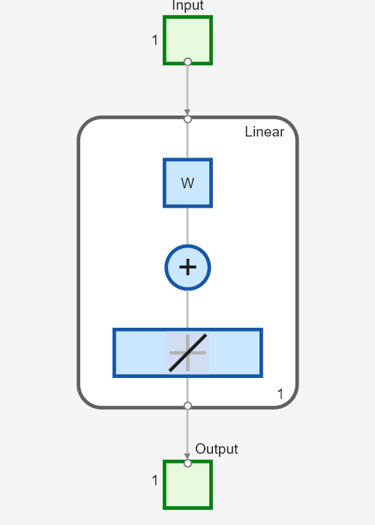
ここで、パルス入力に対するネットワーク応答のシミュレーションを行い、プロットします。

a = net(p);
stem(cell2mat(a))

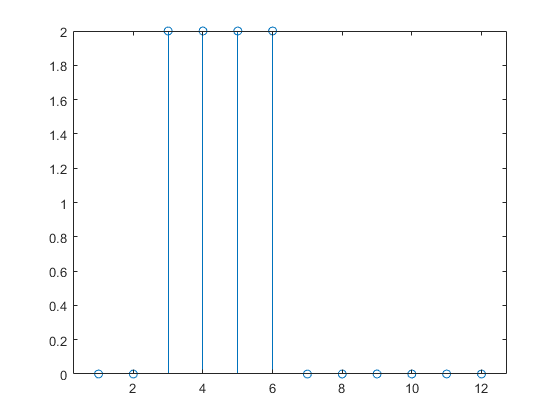
静的ネットワークの応答は入力パルスと同じだけ継続することに注意してください。任意の時点での静的ネットワークの応答は、同じ時点における入力シーケンスの値のみに依存します。

次に、フィードバック結合のない動的ネットワーク (非再帰型ネットワーク) を作成します。動的ネットワークでの同時入力によるシミュレーションで使用したものと同じネットワーク、つまり、入力にタップ付き遅延線のある線形ネットワークを使用できます。

net = linearlayer([0 1]);
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.IW{1,1} = [1 1];

view(net)

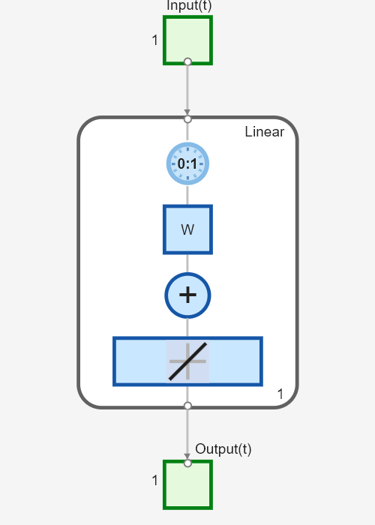
パルス入力に対するネットワーク応答のシミュレーションを再度行い、プロットします。

a = net(p);
stem(cell2mat(a))

動的ネットワークの応答は入力パルスより長く継続します。動的ネットワークには記憶があります。任意の時点での応答は、現在の入力だけでなく入力シーケンスの履歴にも依存します。ネットワークにフィードバック結合がない場合、有限の量の履歴のみが応答に影響を与えます。この図からわかるように、パルスに対する応答は、パルスの持続時間よりも 1 タイムステップ長く継続します。これは、入力のタップ付き遅延線に最大遅延 1 があるためです。

今度は、次の図に示すシンプルな再帰型動的ネットワークについて考えます。

次のコマンドを使用して、ネットワークを作成、表示、シミュレーションできます。narxnet コマンドについては時系列 NARX フィードバックニューラルネットワークの設計で説明しています。

net = narxnet(0,1,[],'closed');
net.inputs{1}.size = 1;
net.layers{1}.dimensions = 1;
net.biasConnect = 0;
net.LW{1} = .5;
net.IW{1} = 1;
view(net)

次のコマンドで、ネットワーク応答をプロットします。

a = net(p);
stem(cell2mat(a))

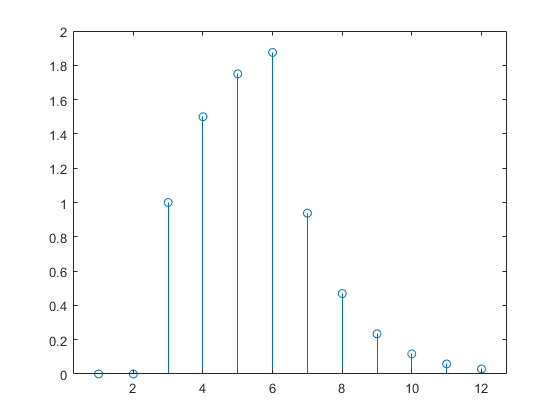
通常、再帰型動的ネットワークは、フィードフォワード動的ネットワークよりも応答が長くなることに注意してください。線形ネットワークの場合、フィードフォワード動的ネットワークは、有限インパルス応答 (FIR) と呼ばれます。これは、インパルス入力に対する応答が一定時間の後に 0 になるためです。線形再帰型動的ネットワークは、無限インパルス応答 (IIR) と呼ばれます。これは、インパルスに対する応答が 0 に向かって減衰しますが (安定したネットワークの場合)、厳密に 0 に等しくなることはないためです。非線形ネットワークのインパルス応答は定義できませんが、有限応答と無限応答の考え方は引き継がれます。

動的ネットワークの応用

一般的に、動的ネットワークは静的ネットワークよりも強力です (ただし、学習が多少難しくなります)。動的ネットワークには記憶があるため、逐次パターンまたは時変パターンを学習できます。これは、金融市場の予測 [RoJa96]、通信システムのチャネルイコライズ [FeTs03]、電力系統の位相検出 [KaGr96]、並べ替え [JaRa04]、故障検出 [ChDa99]、音声認識 [Robin94]、さらに遺伝学におけるタンパク質構造の予測 [GiPr02] などさまざまな分野に応用されています。動的ネットワークの他のさまざまな応用については、[MeJa00] を参照してください。

動的ニューラルネットワークの主要な応用先の 1 つが制御システムです。この応用については、ニューラルネットワーク制御システムで詳しく説明しています。動的ネットワークはフィルター処理にも非常に適しています。このトピックでは、フィルター処理での線形動的ネットワークの使用について説明し、非線形動的ネットワークを使用してその考え方の一部を拡張します。

動的ネットワーク構造

Deep Learning Toolbox™ ソフトウェアは、層状デジタル動的ネットワーク (LDDN) と呼ばれる種類のネットワークに学習させるように設計されています。このツールボックスでは、LDDN の形式に配置できるすべてのネットワークに学習させることができます。ここで、LDDN の基本について説明します。

LDDN の各層は次の部分で構成されます。

その層に入る一連の重み行列 (他の層または外部入力からの結合が可能)、重み行列をその入力に結合させるために使用される関連付けられた重み関数規則 (通常は標準の行列乗算、dotprod)、および関連付けられたタップ付き遅延線
バイアスベクトル
さまざまな重み関数の出力をバイアスと組み合わせて、正味入力を生成するために使用される正味入力関数規則 (通常はサミングジャンクション、netprod)
伝達関数

ネットワークには、入力の重みと呼ばれる特別な重みに結合される入力があり、その重みは IW^i,j (コードでは net.IW{i,j}) で表されます。ここで、j は、その重みを入れる入力ベクトルの番号を表し、i は重みが結合される層の番号を表します。ある層を別の層に結合する重みは、層の重みと呼ばれ、LW^i,j (コードでは net.LW{i,j}) で表されます。ここで、j は、その重みになる層の番号を表し、i は、重みが出力される層の番号を表します。

次の図は 3 層 LDDN の例です。最初の層には、それに関連する 3 つの重みとして、1 つの入力の重み、層 1 からの層の重み、層 3 からの層の重みがあります。2 つの層の重みには、タップ付き遅延線が関連付けられています。

Deep Learning Toolbox ソフトウェアを使用すると、重み関数、正味入力関数、および伝達関数に微分がある限り、LDDN に学習させることができます。よく知られた動的ネットワークアーキテクチャの多くは、LDDN の形式で表すことができます。このトピックの残りの部分では、シンプルなコマンドを使用して非常に強力な動的ネットワークをいくつか作成し、学習させる方法について説明します。このトピックで扱わない他の LDDN ネットワークは、浅層ニューラルネットワークアーキテクチャの定義で説明されているように、汎用のネットワークコマンドを使用して作成できます。

動的ネットワークの学習

Deep Learning Toolbox ソフトウェアでは、動的ネットワークの学習に、浅層の多層ニューラルネットワークと逆伝播学習で説明したものと同じ勾配ベースのアルゴリズムを使用します。そのトピックで紹介された学習関数のいずれも選択できます。以降の節で例を示します。

動的ネットワークの学習には、静的ネットワークの場合と同じ勾配ベースのアルゴリズムを使用できますが、動的ネットワークでのアルゴリズムの性能はかなり異なる場合があり、より複雑な方法で勾配を計算しなければなりません。次の図に示すシンプルな再帰型ネットワークを再び考えます。

重みには、ネットワーク出力に対して 2 つの異なる効果があります。1 つ目は直接的な効果であり、重みの変化により、現在のタイムステップの出力にすぐに生じる変化です (この 1 つ目の効果は、標準の逆伝播を使用して計算できます)。2 つ目は間接的な効果であり、a(t − 1) など、層への入力の一部も重みの関数であることから生じます。この間接的な効果を考慮するには、動的な逆伝播を使用して勾配を計算しなければならず、計算量がより多くなります ([DeHa01a]、[DeHa01b]、および [DeHa07] を参照)。1 つにはこの理由から、動的な逆伝播では学習に時間がかかることが想定されます。また、動的ネットワークの誤差曲面は、静的ネットワークの場合よりも複雑になる可能性があります。学習は局所的最小値により陥り易くなります。これは、最適な結果を実現するには、ネットワークに複数回学習させることが必要になる場合があることを示しています。動的ネットワークの学習に関する説明については、[DHH01] および [HDH09] を参照してください。

このトピックの残りの節では、特定の動的ネットワークを作成して学習を行い、そのネットワークをモデル化、検出、および予測の問題に適用する方法について説明します。ネットワークによっては勾配の計算に動的な逆伝播が必要ですが、不要なものもあります。動的な逆伝播が必要かどうかをユーザーが判断する必要はありません。これは、ソフトウェアで自動的に決定され、使用に最適な形式の動的な逆伝播も判断されます。必要なのは、ネットワークを作成し、標準の train コマンドを呼び出すことだけです。