時系列 NARX フィードバック ニューラル ネットワークの設計
開ループ形式、閉ループ形式、および開/閉ループ複数ステップ予測で適用されている NARX ネットワークの使用例については、ニューラル ネットワークの複数ステップの予測を参照してください。
メモ
NARX モデルを設計するには、System Identification Toolbox™ を使用することもできます。このワークフローは、次の利点があるため推奨されます。
ウェーブレット ネットワーク、機械学習アルゴリズム、ニューラル ネットワークなどの柔軟な非線形関数を使用し、線形 ARX モデルを拡張して複雑な非線形動作をモデル化できる。
適切なリグレッサーを選択して線形モデルから始めることで、洞察と物理情報をシステムに組み込むことができる。
ここまでに説明した具体的な動的ネットワークはすべて、入力層のみにダイナミクスが含まれる集中ネットワークまたはフィードフォワード ネットワークでした。外生入力を伴う非線形自己回帰ネットワーク (NARX) は、ネットワークの複数の層を内包するフィードバック結合のある再帰型動的ネットワークです。NARX モデルは、時系列のモデル化でよく使用される線形 ARX モデルに基づきます。
NARX モデルの定義式は次のとおりです。
ここで、従属的な出力信号 y(t) の次の値は、それ以前の出力信号の値、およびそれ以前の独立した (外生) 入力信号の値に対し遡及されています。NARX モデルは、フィードフォワード ニューラル ネットワークを使用して関数 f を近似することで実装できます。結果として得られるネットワークの図を以下に示します。ここでは、2 層フィードフォワード ネットワークを近似のために使用しています。この実装はベクトル ARX モデルにも使用できます。その場合、入力と出力は多次元になる可能性があります。
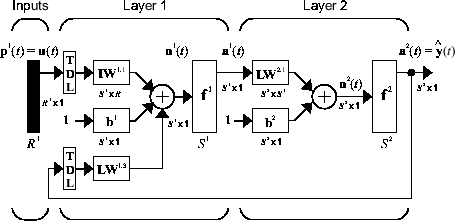
NARX ネットワークにはさまざまな用途があります。予測子として使用して、入力信号の次の値を予測できます。非線形フィルター処理にも使用できます。その場合、ターゲット出力は入力信号からノイズを除去したものとなります。NARX ネットワークは、別の重要な用途である非線形動的システムのモデル化でも使用されています。
NARX ネットワークの学習の説明の前に、学習に役立つある重要な構成について説明が必要です。NARX ネットワークの出力は、モデル化する非線形動的システムの出力の推定と考えることができます。以下の左側の図に示すように、出力は、標準的な NARX アーキテクチャの一部としてフィードフォワード ニューラル ネットワークの入力にフィードバックされます。ネットワークの学習中は真の出力が使用できるため、直並列アーキテクチャを作成できます ([NaPa91] を参照)。この場合、以下の右側の図に示すように、推定された出力をフィードバックするのではなく、真の出力が使用されます。これには 2 つの利点があります。1 つ目は、フィードフォワード ネットワークへの入力の精度が高くなることです。2 つ目は、結果として得られるネットワークが純粋なフィードフォワード アーキテクチャを持つようになり、静的な逆伝播を学習に使用できることです。
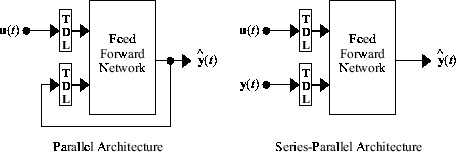
次に、動的システムをモデル化するための NARX ネットワークの学習における、直並列アーキテクチャの使用を示します。
NARX ネットワークの例は、NARMA-L2 Controller ブロックの使用の最初で説明している磁気浮上システムです。次の図にある下のグラフは電磁石に印加される電圧を示し、上のグラフは永久磁石の位置を示しています。データは 0.01 秒のサンプリング間隔で収集され、2 つの時系列が形成されました。
目標は、この磁気浮上システムの NARX モデルの作成です。
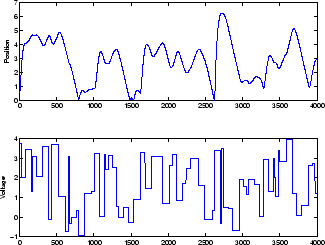
まず、学習データを読み込みます。入力と出力の両方に 2 つの遅延があるタップ付き遅延線を使用します。つまり、学習は 3 番目のデータ点から始まります。直並列ネットワークへの 2 つの入力として、u(t) シーケンスと y(t) シーケンスがあります。
[u,y] = maglev_dataset;
関数 narxnet を使用して、直並列 NARX ネットワークを作成します。隠れ層で 10 個のニューロンを使用し、学習関数として trainlm を使用します。さらに、preparets を使用してデータを準備します。
d1 = [1:2];
d2 = [1:2];
narx_net = narxnet(d1,d2,10);
narx_net.divideFcn = '';
narx_net.trainParam.min_grad = 1e-10;
[p,Pi,Ai,t] = preparets(narx_net,u,{},y);
(y シーケンスは、入力であり出力 (ターゲット) でもあるフィードバック信号と見なされることに注意してください。後で、ループを閉じるとき、適切な出力が適切な入力に結合されます。) これでネットワークの学習の準備が整いました。
narx_net = train(narx_net,p,t,Pi);

ネットワークのシミュレーションを行い、結果として得られる直並列実装の誤差をプロットできます。
yp = sim(narx_net,p,Pi); e = cell2mat(yp)-cell2mat(t); plot(e)

誤差が非常に小さいことを確認できます。ただし、直並列構成であるため、これらは 1 ステップ先の予測の場合の誤差です。より厳密なテストを行うには、ネットワークを元の並列形式 (閉ループ) に再配置してから、多数のタイム ステップにわたって反復予測を実行します。これで、並列動作が示されます。
NARX (および他の) ネットワークを、学習に便利な直並列構成 (開ループ) から複数ステップ先の予測に役立つ並列構成 (閉ループ) に変換するためのツールボックス関数 (closeloop) があります。次のコマンドは、先ほど学習させたネットワークを並列形式に変換する方法を説明するものです。
narx_net_closed = closeloop(narx_net);
2 つのネットワークの違いを確認するには、表示コマンドを使用します。
view(narx_net)

view(narx_net_closed)
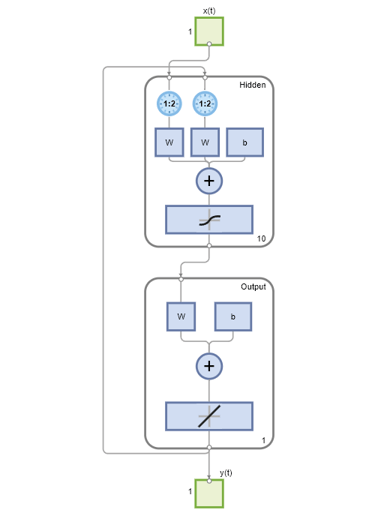
検証ステップおよびテスト ステップを含むすべての学習が、開ループ (直並列アーキテクチャとも呼ばれます) で行われています。典型的なワークフローでは、ネットワークを完全に開ループで作成し、(検証ステップおよびテスト ステップを含めて) このネットワークの学習を行った後でのみ、複数ステップ先の予測を行うために閉ループに変換します。同様に、開ループの学習結果に基づいて、GUI の R 値が計算されます。
次に、閉ループ (並列) 構成を使用して、900 タイム ステップの反復予測を実行します。このネットワークでは、初期条件として 2 つの初期入力と 2 つの初期出力を読み込む必要があります。データの準備には関数 preparets が使用できます。これは、ネットワーク構造を使用して、データを適切に分割およびシフトする方法を決定します。
y1 = y(1700:2600);
u1 = u(1700:2600);
[p1,Pi1,Ai1,t1] = preparets(narx_net_closed,u1,{},y1);
yp1 = narx_net_closed(p1,Pi1,Ai1);
TS = size(t1,2);
plot(1:TS,cell2mat(t1),'b',1:TS,cell2mat(yp1),'r')

この図は反復予測を示しています。青い線は磁石の実際の位置で、赤い線は NARX ニューラル ネットワークで予測された位置です。このネットワークは 900 タイム ステップ先を予測していますが、予測は非常に正確です。
正確な並列応答 (反復予測) を実現するには、直並列構成 (1 ステップ先の予測) の誤差が非常に小さくなるようにネットワークに学習させることが重要です。
また、narxnet コマンドを使用して 4 番目の入力引数を 'closed' に設定することで並列 (閉ループ) NARX ネットワークを作成し、そのネットワークに直接学習させることもできます。一般的に、この学習には時間がかかり、結果として得られる性能も直並列の学習で得られる性能ほどよくありません。
ニューラル ネットワークでは、学習を行うたびに異なる解が得られる可能性がありますが、これは初期の重みとバイアスの値が異なり、データの学習セット、検証セット、テスト セットへの分割が異なるためです。このため、別のニューラル ネットワークが同じ問題について学習した場合、入力が同じでも出力が異なる場合があります。ニューラル ネットワークで高い精度が得られるようにするためには、何度か再学習を行います。
高い精度が必要な場合は、初期解を改善するための手法が他にいくつかあります。詳細については、浅層ニューラル ネットワークの汎化の改善と過適合の回避を参照してください。
複数の外部変数
磁気浮上の例では、常に外部入力値が 1 つの場合について、時系列をモデル化する方法を説明しました。しかし、NARX ネットワークは、複数の外部入力要素を持つ問題に使用して、複数の要素を含む系列を予測できます。その場合、入力とターゲットは時間を表す行 cell 配列で構成されますが、各 cell 要素は入力信号またはターゲット信号の N 個の要素に対応する N 行 1 列ベクトルです。
たとえば、次は 1 要素系列を予測する 2 要素外部変数で構成されるデータセットです。
[X,T] = ph_dataset;
外部入力 X の形式は 2 要素ベクトルの行 cell 配列で、各ベクトルは酸と塩基の溶液の流れを表します。ターゲットは、時間の経過と共に得られる溶液の pH を表します。
関数 con2seq を使用すると、独自の多要素系列データを行列形式からニューラル ネットワーク時系列形式に再構築できます。
ネットワークの学習プロセスは、前述の磁気浮上の問題と同様に進みます。
net = narxnet(10);
[x,xi,ai,t] = preparets(net,X,{},T);
net = train(net,x,t,xi,ai);
y = net(x,xi,ai);
e = gsubtract(t,y); 開ループ形式、閉ループ形式、および開/閉ループ複数ステップ予測で適用されている NARX ネットワークの使用例については、ニューラル ネットワークの複数ステップの予測を参照してください。