多層ニューラル ネットワークの学習関数の選択
与えられた問題に対して、どの学習アルゴリズムが最も高速であるかを判断するのは、とても難しいことです。これは、問題の複雑度、学習セット内のデータ点数、ネットワークの重みやバイアスの数、誤差の目標値のほか、ネットワークをパターン認識 (判別分析) に利用するのか、あるいは関数近似 (回帰) に利用するのかなど、さまざまな要因に左右されます。この節では、さまざまな学習アルゴリズムを比較します。6 つの異なる問題について、フィードフォワード ネットワークの学習を行います。このうち 3 つの問題はパターン認識のカテゴリに属し、他の 3 つは関数近似のカテゴリに属します。2 つの問題はシンプルな "トイ プロブレム" であり、他の 4 つの問題は "実世界" の問題です。アーキテクチャや複雑度が異なるネットワークが使用され、ネットワークはさまざまな精度レベルまで学習が行われます。
次の表は、テストしたアルゴリズムとそれらを識別するために使用する頭字語の一覧です。
頭字語 | アルゴリズム | 説明 |
|---|---|---|
LM | trainlm | レーベンバーグ・マルカート法 |
BFG | trainbfg | BFGS 準ニュートン法 |
RP | trainrp | 弾性逆伝播法 |
SCG | trainscg | スケーリング共役勾配法 |
CGB | traincgb | Powell・Beale リスタート付き共役勾配法 |
CGF | traincgf | Fletcher・Powell 共役勾配法 |
CGP | traincgp | Polak・Ribiére 共役勾配法 |
OSS | trainoss | 1 ステップ割線法 |
GDX | traingdx | 可変学習率逆伝播法 |
次の表に、6 つのベンチマーク問題と、使用したネットワーク、学習プロセス、コンピューターのいくつかの特徴を示します。
問題のタイトル | 問題のタイプ | ネットワーク構造 | 誤差の目標値 | コンピューター |
|---|---|---|---|---|
SIN | 関数近似 | 1-5-1 | 0.002 | Sun Sparc 2 |
PARITY | パターン認識 | 3-10-10-1 | 0.001 | Sun Sparc 2 |
ENGINE | 関数近似 | 2-30-2 | 0.005 | Sun Enterprise 4000 |
CANCER | パターン認識 | 9-5-5-2 | 0.012 | Sun Sparc 2 |
CHOLESTEROL | 関数近似 | 21-15-3 | 0.027 | Sun Sparc 20 |
DIABETES | パターン認識 | 8-15-15-2 | 0.05 | Sun Sparc 20 |
SIN データ セット
最初のベンチマーク データ セットは、シンプルな関数近似問題です。隠れ層に伝達関数 tansig、出力層に線形伝達関数を使用した 1-5-1 ネットワークを、1 周期の正弦波の近似に使用しています。次の表は、9 つの異なる学習アルゴリズムを使用してこのネットワークの学習を行った結果をまとめたものです。この表の各エントリは、試行ごとに異なるランダムな初期重みを使用し、30 回繰り返し試行を行った結果を表しています。どの場合も、ネットワークは、二乗誤差が 0.002 未満になるまで学習が行われています。この問題に対して最も高速なアルゴリズムは、レーベンバーグ・マルカート法アルゴリズムです。平均では、2 番目に高速なアルゴリズムに比べて 4 倍超も高速です。この問題のように、ネットワークの重みの数が 100 未満で、近似にかなりの精度が求められる関数近似問題については、LM アルゴリズムが最も適しています。
アルゴリズム | 平均時間 (秒) | 比率 | 最小時間 (秒) | 最大時間 (秒) | 標準偏差 (秒) |
|---|---|---|---|---|---|
LM | 1.14 | 1.00 | 0.65 | 1.83 | 0.38 |
BFG | 5.22 | 4.58 | 3.17 | 14.38 | 2.08 |
RP | 5.67 | 4.97 | 2.66 | 17.24 | 3.72 |
SCG | 6.09 | 5.34 | 3.18 | 23.64 | 3.81 |
CGB | 6.61 | 5.80 | 2.99 | 23.65 | 3.67 |
CGF | 7.86 | 6.89 | 3.57 | 31.23 | 4.76 |
CGP | 8.24 | 7.23 | 4.07 | 32.32 | 5.03 |
OSS | 9.64 | 8.46 | 3.97 | 59.63 | 9.79 |
GDX | 27.69 | 24.29 | 17.21 | 258.15 | 43.65 |
さまざまなアルゴリズムの性能は、近似に求められる精度の影響を受けます。これを以下の図に示しています。この図は、いくつかの代表的なアルゴリズムについて、実行時間 (30 回の試行の平均) に対する平均二乗誤差をプロットしたものです。ここでは、LM アルゴリズムの誤差は、他のアルゴリズムと比べて短時間で急速に減少していることがわかります。
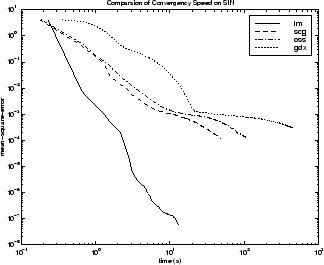
アルゴリズム間の関係については、以下の図に詳しく示しています。この図は、平均二乗誤差の収束目標値に対する収束にかかる時間をプロットしたものです。ここでは、誤差の目標値が小さくなるにつれて、LM アルゴリズムによる改善が顕著になることがわかります。一部のアルゴリズム (LM と BFG) は誤差の目標値が小さくなるにつれて性能が向上しますが、他のアルゴリズム (OSS と GDX) は誤差の目標値が小さくなるにつれて性能が低下しています。

PARITY データ セット
2 番目のベンチマーク問題は、3 ビット数値のパリティを検出するシンプルなパターン認識問題です。入力パターンの 1 の数が奇数個であれば、ネットワークは 1 を出力し、そうでなければ -1 を出力します。この問題に使用するネットワークは、各層に tansig ニューロンを使用した 3-10-10-1 ネットワークです。次の表は、9 つの異なるアルゴリズムを使用してこのネットワークの学習を行った結果をまとめたものです。この表の各エントリは、試行ごとに異なるランダムな初期重みを使用し、30 回繰り返し試行を行った結果を表しています。どの場合も、ネットワークは、二乗誤差が 0.001 未満になるまで学習が行われています。この問題に対して最も高速なアルゴリズムは弾性逆伝播法アルゴリズムで、共役勾配法アルゴリズム (特にスケーリング共役勾配法アルゴリズム) もほぼ同じくらい高速です。LM アルゴリズムは、この問題に対する性能はあまり良くないことに注意してください。一般的に、LM アルゴリズムは、パターン認識問題において、関数近似問題ほど良い性能を発揮しません。LM アルゴリズムは、ほぼ線形である最小二乗問題向けに設計されています。パターン認識問題における出力ニューロンは一般的に飽和しているので、線形領域では効果がありません。
アルゴリズム | 平均時間 (秒) | 比率 | 最小時間 (秒) | 最大時間 (秒) | 標準偏差 (秒) |
|---|---|---|---|---|---|
RP | 3.73 | 1.00 | 2.35 | 6.89 | 1.26 |
SCG | 4.09 | 1.10 | 2.36 | 7.48 | 1.56 |
CGP | 5.13 | 1.38 | 3.50 | 8.73 | 1.05 |
CGB | 5.30 | 1.42 | 3.91 | 11.59 | 1.35 |
CGF | 6.62 | 1.77 | 3.96 | 28.05 | 4.32 |
OSS | 8.00 | 2.14 | 5.06 | 14.41 | 1.92 |
LM | 13.07 | 3.50 | 6.48 | 23.78 | 4.96 |
BFG | 19.68 | 5.28 | 14.19 | 26.64 | 2.85 |
GDX | 27.07 | 7.26 | 25.21 | 28.52 | 0.86 |
関数近似問題と同様に、さまざまなアルゴリズムの性能は、ネットワークで求められる精度の影響を受けます。これを以下の図に示しています。この図は、いくつかの代表的なアルゴリズムについて、実行時間に対する平均二乗誤差をプロットしたものです。LM アルゴリズムは、ある点から急速に収束しますが、収束するのは他のアルゴリズムが既に収束した後です。
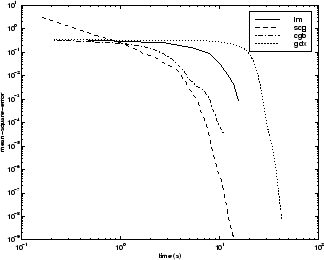
アルゴリズム間の関係については、以下の図に詳しく示しています。この図は、平均二乗誤差の収束目標値に対する収束にかかる時間をプロットしたものです。ここでも、一部のアルゴリズム (OSS と BFG) は誤差の目標値が小さくなるにつれて性能が低下することがわかります。
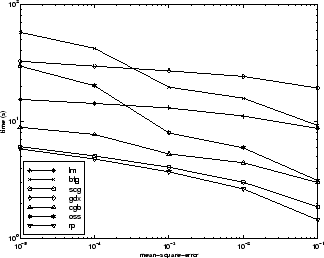
ENGINE データ セット
3 番目のベンチマーク問題は、現実的な関数近似 (つまり非線形回帰) の問題です。データは、エンジンの作動状況から取得したものです。ネットワークの入力はエンジン速度と燃料レベルで、ネットワークの出力はトルクと排気レベルです。この問題に使用するネットワークは、隠れ層に tansig ニューロン、出力層に線形ニューロンを使用した 2-30-2 ネットワークです。次の表は、9 つの異なるアルゴリズムを使用してこのネットワークの学習を行った結果をまとめたものです。この表の各エントリは、試行ごとに異なるランダムな初期重みを使用し、30 回 (RP と GDX は時間制約のため 10 回) 繰り返し試行を行った結果を表しています。どの場合も、ネットワークは、二乗誤差が 0.005 未満になるまで学習が行われています。この問題に対して最も高速なアルゴリズムは LM アルゴリズムで、BFGS 準ニュートン アルゴリズムと共役勾配法アルゴリズムがそれに続きます。この問題は関数近似問題ですが、SIN データ セットのときほど、LM アルゴリズムが明確に優れているとは言えません。この場合は、ネットワークの重みとバイアスの数は、SIN 問題と比較すると非常に多くなっており (152 対 16)、ネットワーク パラメーターの数が増えるにつれて、LM アルゴリズムの有効性は低くなります。
アルゴリズム | 平均時間 (秒) | 比率 | 最小時間 (秒) | 最大時間 (秒) | 標準偏差 (秒) |
|---|---|---|---|---|---|
LM | 18.45 | 1.00 | 12.01 | 30.03 | 4.27 |
BFG | 27.12 | 1.47 | 16.42 | 47.36 | 5.95 |
SCG | 36.02 | 1.95 | 19.39 | 52.45 | 7.78 |
CGF | 37.93 | 2.06 | 18.89 | 50.34 | 6.12 |
CGB | 39.93 | 2.16 | 23.33 | 55.42 | 7.50 |
CGP | 44.30 | 2.40 | 24.99 | 71.55 | 9.89 |
OSS | 48.71 | 2.64 | 23.51 | 80.90 | 12.33 |
RP | 65.91 | 3.57 | 31.83 | 134.31 | 34.24 |
GDX | 188.50 | 10.22 | 81.59 | 279.90 | 66.67 |
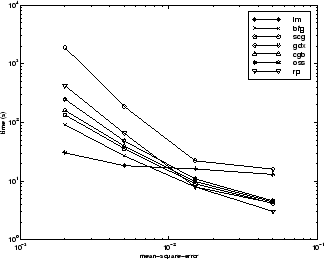
次の図は、いくつかの代表的なアルゴリズムについて、実行時間に対する平均二乗誤差をプロットしたものです。LM アルゴリズムの性能は、他のアルゴリズムよりも時間の経過に合わせて向上しています。
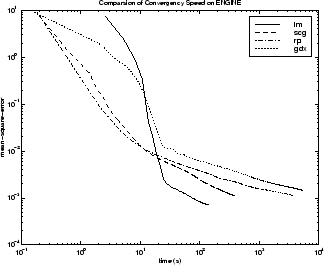
アルゴリズム間の関係については、以下の図に詳しく示しています。この図は、平均二乗誤差の収束目標値に対する収束にかかる時間をプロットしたものです。ここでも、誤差の目標値が小さくなるにつれて、LM アルゴリズムの性能は向上する一方で、一部のアルゴリズム (GDX と RP) は性能が低下することがわかります。
CANCER データ セット
4 番目のベンチマーク問題は、現実的なパターン認識 (つまり非線形判別分析) の問題です。ネットワークの目的は、顕微鏡検査によって収集された細胞データから、腫瘍を良性と悪性に分類することです。入力の属性には、細胞塊の厚さ、細胞の大きさや形状の均一性、周縁部癒着量、裸核の頻度が含まれます。データは、ウィスコンシン大学マディソン校病院の William H. Wolberg 博士からご提供いただきました。この問題に使用するネットワークは、すべての層に tansig ニューロンを使用する 9-5-5-2 ネットワークです。次の表は、9 つの異なるアルゴリズムを使用してこのネットワークの学習を行った結果をまとめたものです。この表の各エントリは、試行ごとに異なるランダムな初期重みを使用し、30 回繰り返し試行を行った結果を表しています。どの場合も、ネットワークは、二乗誤差が 0.012 未満になるまで学習が行われています。いくつかのアルゴリズムでは収束しなかった実行が少数あったため、各アルゴリズムの実行のうち上位 75% だけを統計量の取得に使用しています。
共役勾配法アルゴリズムと弾性逆伝播法アルゴリズムは全般的に収束が速く、LM アルゴリズムもかなり高速です。PARITY データ セットと同様に、LM アルゴリズムは、パターン認識問題において、関数近似問題ほど良い性能を発揮しません。
アルゴリズム | 平均時間 (秒) | 比率 | 最小時間 (秒) | 最大時間 (秒) | 標準偏差 (秒) |
|---|---|---|---|---|---|
CGB | 80.27 | 1.00 | 55.07 | 102.31 | 13.17 |
RP | 83.41 | 1.04 | 59.51 | 109.39 | 13.44 |
SCG | 86.58 | 1.08 | 41.21 | 112.19 | 18.25 |
CGP | 87.70 | 1.09 | 56.35 | 116.37 | 18.03 |
CGF | 110.05 | 1.37 | 63.33 | 171.53 | 30.13 |
LM | 110.33 | 1.37 | 58.94 | 201.07 | 38.20 |
BFG | 209.60 | 2.61 | 118.92 | 318.18 | 58.44 |
GDX | 313.22 | 3.90 | 166.48 | 446.43 | 75.44 |
OSS | 463.87 | 5.78 | 250.62 | 599.99 | 97.35 |
次の図は、いくつかの代表的なアルゴリズムについて、実行時間に対する平均二乗誤差をプロットしたものです。この問題では、これまでの問題で見られたような、性能の大きな違いは見られません。
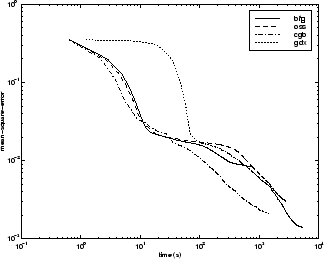
アルゴリズム間の関係については、以下の図に詳しく示しています。この図は、平均二乗誤差の収束目標値に対する収束にかかる時間をプロットしたものです。ここでも、誤差の目標値が小さくなるにつれて、LM アルゴリズムの性能は向上する一方で、一部のアルゴリズム (OSS と BFG) は性能が低下することがわかります。誤差の目標値が小さくなるにつれて他のアルゴリズムよりも性能が向上するという点は、すべての問題において LM アルゴリズムの典型的な性質です。
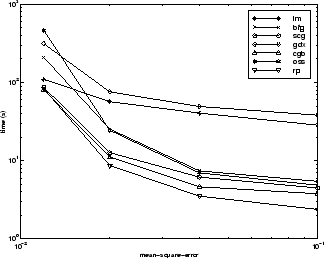
CHOLESTEROL データ セット
5 番目のベンチマーク問題は、現実的な関数近似 (または非線形回帰) 問題です。ネットワークの目的は、21 個のスペクトル成分の測定値に基づいて、コレステロール レベル (ldl、hdl、vldl) を予測することです。データは、オクラホマ州立大学化学科の Neil Purdie 博士 [PuLu92] からご提供いただきました。この問題に使用するネットワークは、隠れ層に tansig ニューロン、出力層に線形ニューロンを使用した 21-15-3 ネットワークです。次の表は、9 つの異なるアルゴリズムを使用してこのネットワークの学習を行った結果をまとめたものです。この表の各エントリは、試行ごとに異なるランダムな初期重みを使用し、30 回 (RP と GDX は 10 回) 繰り返し試行を行った結果を表しています。どの場合も、ネットワークは、二乗誤差が 0.027 未満になるまで学習が行われています。
どの共役勾配法アルゴリズムも優れた性能を示していますが、スケーリング共役勾配法アルゴリズムはこの問題に対して最も優れた性能を発揮しています。LM アルゴリズムは、この関数近似問題に対して、他の 2 つの関数近似問題ほど良い性能を発揮しません。これは、ネットワークの重みとバイアスの数がまた増えたからです (378 対 152 対 16)。パラメーターの数が増えるにつれて、LM アルゴリズムで必要となる計算量は幾何級数的に増加します。
アルゴリズム | 平均時間 (秒) | 比率 | 最小時間 (秒) | 最大時間 (秒) | 標準偏差 (秒) |
|---|---|---|---|---|---|
SCG | 99.73 | 1.00 | 83.10 | 113.40 | 9.93 |
CGP | 121.54 | 1.22 | 101.76 | 162.49 | 16.34 |
CGB | 124.06 | 1.2 | 107.64 | 146.90 | 14.62 |
CGF | 136.04 | 1.36 | 106.46 | 167.28 | 17.67 |
LM | 261.50 | 2.62 | 103.52 | 398.45 | 102.06 |
OSS | 268.55 | 2.69 | 197.84 | 372.99 | 56.79 |
BFG | 550.92 | 5.52 | 471.61 | 676.39 | 46.59 |
RP | 1519.00 | 15.23 | 581.17 | 2256.10 | 557.34 |
GDX | 3169.50 | 31.78 | 2514.90 | 4168.20 | 610.52 |
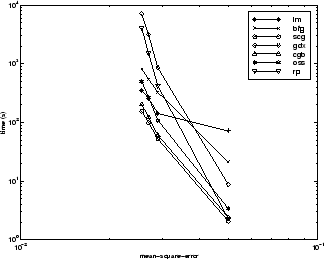
次の図は、いくつかの代表的なアルゴリズムについて、実行時間に対する平均二乗誤差をプロットしたものです。この問題では、LM アルゴリズムが他のアルゴリズムより、平均二乗誤差をより減少させられることがわかります。SCG アルゴリズムと RP アルゴリズムは最も早く初期収束します。
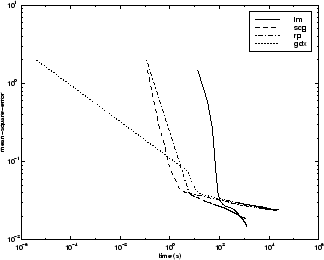
アルゴリズム間の関係については、以下の図に詳しく示しています。この図は、平均二乗誤差の収束目標値に対する収束にかかる時間をプロットしたものです。誤差の目標値が小さくなるにつれて、LM アルゴリズムと BFG アルゴリズムは他のアルゴリズムよりも性能が向上していることがわかります。
DIABETES データ セット
6 番目のベンチマーク問題は、パターン認識問題です。ネットワークの目的は、個人データ (年齢、妊娠回数) と健康診断の結果 (血圧、ボディマス指数、ブドウ糖負荷試験の結果など) に基づいて糖尿病かどうかを判定することです。データは、カリフォルニア大学アービン校の機械学習データベースから取得しました。この問題に使用するネットワークは、すべての層に tansig ニューロンを使用する 8-15-15-2 ネットワークです。次の表は、9 つの異なるアルゴリズムを使用してこのネットワークの学習を行った結果をまとめたものです。この表の各エントリは、試行ごとに異なるランダムな初期重みを使用し、10 回繰り返し試行を行った結果を表しています。どの場合も、ネットワークは、二乗誤差が 0.05 未満になるまで学習が行われています。
共役勾配法アルゴリズムと弾性逆伝播法アルゴリズムは全般的に収束が速くなっています。この問題の結果は、これまでに取り上げた他のパターン認識問題の結果と整合性が取れています。RP アルゴリズムは、すべてのパターン認識問題において良い結果を示しています。これは、このアルゴリズムが、中心点から遠いところで非常に緩やかな傾きを持つシグモイド関数を使用した学習に起因する困難な問題を克服するよう設計されているため、妥当な結果と言えます。パターン認識問題では、出力層にシグモイド伝達関数を使用し、シグモイド関数の両端でもネットワークが機能する必要があります。
アルゴリズム | 平均時間 (秒) | 比率 | 最小時間 (秒) | 最大時間 (秒) | 標準偏差 (秒) |
|---|---|---|---|---|---|
RP | 323.90 | 1.00 | 187.43 | 576.90 | 111.37 |
SCG | 390.53 | 1.21 | 267.99 | 487.17 | 75.07 |
CGB | 394.67 | 1.22 | 312.25 | 558.21 | 85.38 |
CGP | 415.90 | 1.28 | 320.62 | 614.62 | 94.77 |
OSS | 784.00 | 2.42 | 706.89 | 936.52 | 76.37 |
CGF | 784.50 | 2.42 | 629.42 | 1082.20 | 144.63 |
LM | 1028.10 | 3.17 | 802.01 | 1269.50 | 166.31 |
BFG | 1821.00 | 5.62 | 1415.80 | 3254.50 | 546.36 |
GDX | 7687.00 | 23.73 | 5169.20 | 10350.00 | 2015.00 |
次の図は、いくつかの代表的なアルゴリズムについて、実行時間に対する平均二乗誤差をプロットしたものです。他の問題と同様に、SCG と RP は速く初期収束しますが、LM アルゴリズムは最終的な誤差がより小さくなります。
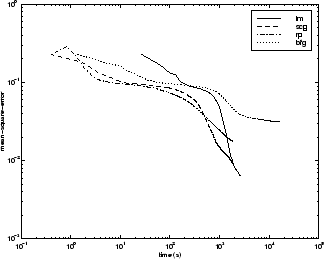
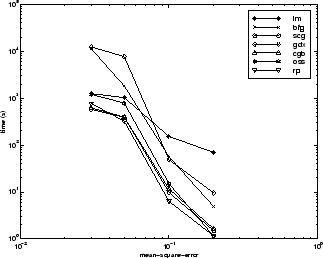
アルゴリズム間の関係については、以下の図に詳しく示しています。この図は、平均二乗誤差の収束目標値に対する収束にかかる時間をプロットしたものです。ここでも、誤差の目標値が小さくなるにつれて、LM アルゴリズムの性能は向上する一方で、BFG アルゴリズムは性能が低下することがわかります。RP アルゴリズムは、誤差の目標値については最小ではなく SCG の方が優れていますが、性能が最も優れています。
まとめ
これまで述べてきた実験から推測できるアルゴリズムの特性がいくつかあります。一般的に、関数近似問題において、最大で数百個の重みを持つネットワークでは、レーベンバーグ・マルカート法アルゴリズムが最も速く収束します。この有効性が特に顕著なのは、非常に高い精度で学習を行う必要がある場合です。多くの場合、trainlm は、テストした他のどのアルゴリズムよりも小さな平均二乗誤差を得ることができます。しかし、ネットワークの重みの数が増加するにつれて、trainlm の有効性は低くなります。また、trainlm の性能は、パターン認識問題に対してはあまり良くありません。trainlm のストレージ要件は、テストした他のアルゴリズムよりも大きくなっています。
関数 trainrp は、パターン認識問題に対して最も高速なアルゴリズムです。しかし、関数近似問題では良い性能を発揮しません。誤差の目標値が小さくなるにつれてその性能も低下します。このアルゴリズムのメモリ要件は、取り上げた他のアルゴリズムと比べて比較的小さくなっています。
共役勾配法アルゴリズム、中でも trainscg は、幅広い問題に対して良い性能を発揮し、特に重みの数が多いネットワークにおいてはそれが顕著であるように見えます。SCG アルゴリズムは、関数近似問題に対して LM アルゴリズムと同じくらい高速 (大きなネットワークでは SCG の方が高速) で、パターン認識問題に対しても trainrp と同じくらいの高速です。誤差が小さくなっても、性能は trainrp ほどすぐに低下することはありません。共役勾配法アルゴリズムは、メモリ要件が比較的厳しくありません。
trainbfg の性能は trainlm の性能と似ています。trainlm ほどストレージを必要としませんが、ネットワーク サイズが大きくなると、必要な計算量が幾何級数的に増加します。これは、逆行列の計算と等価な計算を反復のたびに行わなければならないからです。
可変学習率アルゴリズム traingdx は、通常は他のアルゴリズムよりもかなり遅く、ストレージ要件は trainrp と同じくらいですが、一部の問題に対しては便利なアルゴリズムです。ゆっくり収束した方が良い場合もあります。たとえば、早期停止を使用している場合、収束がとても早いアルゴリズムを使用していると、結果に矛盾が生じることがあります。検証セットの誤差が最小になる点では、オーバーシュートする場合があります。