plotconfusion

分類の混同行列のプロット

構文

plotconfusion(targets,outputs)

plotconfusion(targets,outputs,name)

plotconfusion(targets1,outputs1,name1,targets2,outputs2,name2,...,targetsn,outputsn,namen)

説明

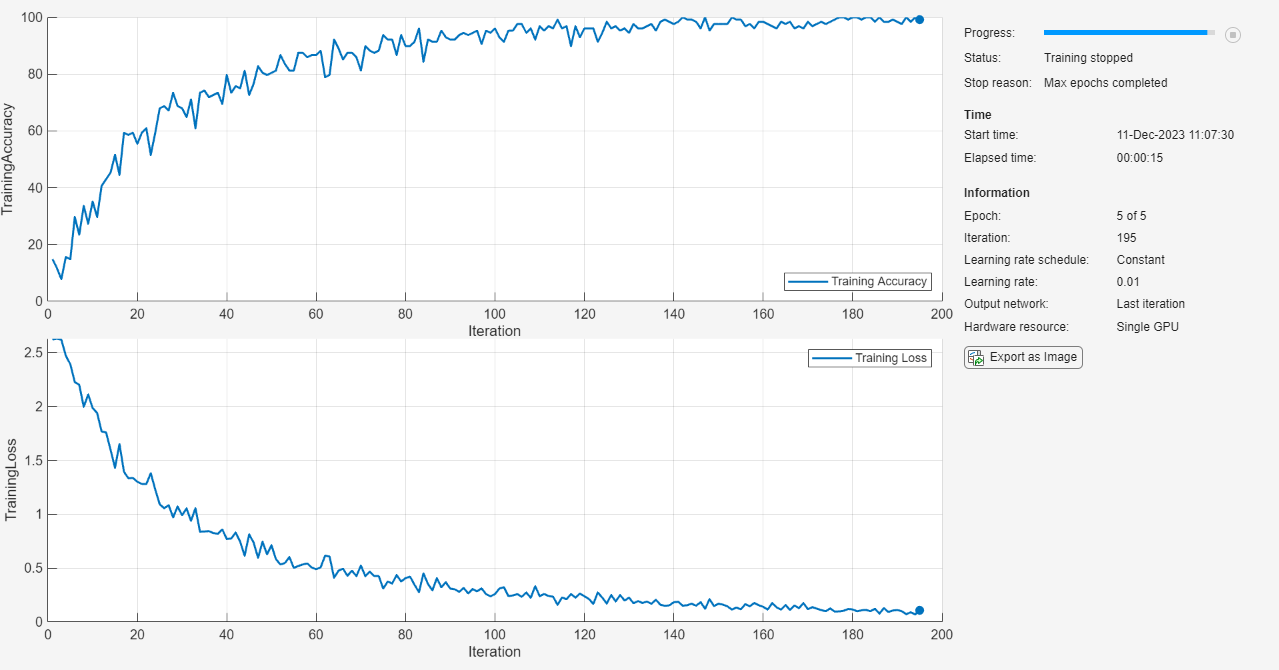
plotconfusion(targets,outputs) は、真のラベル targets および予測ラベル outputs の混同行列をプロットします。ラベルは、categorical ベクトルまたは one-of-N (one-hot) 表現で指定します。

ヒント

plotconfusion は、カテゴリカルラベルでは推奨されません。代わりに confusionchart を使用してください。

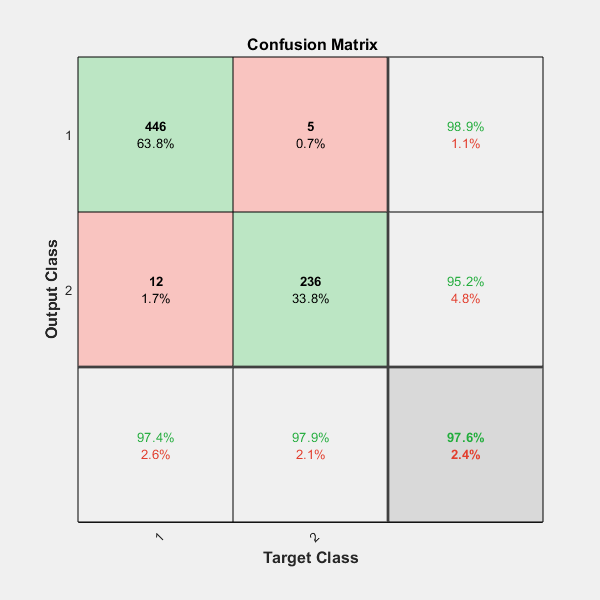
混同行列プロットでは、行は予測されたクラス (出力クラス) に対応し、列は真のクラス (ターゲットクラス) に対応します。対角線上のセルは、正しく分類された観測値に対応します。対角線外のセルは、誤分類された観測値に対応します。観測値の数と観測値の総数に対する割合の両方が各セルに表示されます。

プロットの右端の列は、各クラスに属していると予測されたすべての例について正しく分類された例と誤分類された例の割合を示します。これらのメトリクスは通常、それぞれ精度 (または陽性の予測値) および偽発見率と呼ばれます。プロットの下部の行は、各クラスに属しているすべての例について正しく分類された例と誤分類された例の割合を示します。これらのメトリクスは通常、それぞれ再現率 (または真陽性率) および偽陰性率と呼ばれます。プロットの右下のセルは、全体の精度を示します。

plotconfusion(targets,outputs,name) は混同行列をプロットし、プロットのタイトルの先頭に name を追加します。

plotconfusion(targets1,outputs1,name1,targets2,outputs2,name2,...,targetsn,outputsn,namen) は、1 つの Figure に複数の混同行列をプロットし、対応するプロットのタイトルの先頭に引数 name を追加します。

例

すべて折りたたむ

カテゴリカルラベルを使用した混同行列のプロット

ライブスクリプトを開く

手書き数字の合成イメージで構成されているデータを読み込みます。XTrain はイメージの 28 x 28 x 1 x 5000 配列で、YTrain はイメージラベルを含む categorical ベクトルです。

load DigitsDataTrain
classNames = categories(labelsTrain);

畳み込みニューラルネットワークのアーキテクチャを定義します。

layers = [
    imageInputLayer([28 28 1])
    
    convolution2dLayer(3,8,'Padding','same')
    batchNormalizationLayer
    reluLayer    
    convolution2dLayer(3,16,'Padding','same','Stride',2)
    batchNormalizationLayer
    reluLayer
    convolution2dLayer(3,32,'Padding','same','Stride',2)
    batchNormalizationLayer
    reluLayer
    
    fullyConnectedLayer(10)
    softmaxLayer];

学習オプションを指定し、ネットワークに学習させます。

options = trainingOptions('sgdm', ...
    'MaxEpochs',5, ...
    'Verbose',false, ...
    'Plots','training-progress', ...
    'Metrics','accuracy');
net = trainnet(XTrain,labelsTrain,layers,"crossentropy",options);

テストデータを読み込み、学習済みネットワークを使用して分類します。

load digitsDataTest
scores = minibatchpredict(net,XTest)

scores = 5000×10 single matrix

    0.9979    0.0005    0.0005    0.0001    0.0001    0.0000    0.0004    0.0000    0.0002    0.0002
    0.9297    0.0000    0.0320    0.0003    0.0000    0.0001    0.0017    0.0005    0.0004    0.0353
    0.9996    0.0000    0.0001    0.0000    0.0000    0.0000    0.0001    0.0000    0.0000    0.0002
    0.9195    0.0000    0.0004    0.0001    0.0002    0.0000    0.0147    0.0000    0.0016    0.0635
    0.9429    0.0006    0.0032    0.0003    0.0000    0.0021    0.0040    0.0021    0.0447    0.0002
    0.9906    0.0003    0.0001    0.0000    0.0000    0.0000    0.0003    0.0000    0.0002    0.0085
    0.9938    0.0000    0.0004    0.0000    0.0000    0.0000    0.0011    0.0000    0.0041    0.0006
    0.9998    0.0000    0.0000    0.0000    0.0000    0.0000    0.0001    0.0000    0.0000    0.0000
    0.6722    0.0001    0.0028    0.0002    0.0013    0.0022    0.0007    0.0001    0.0035    0.3168
    0.8069    0.0020    0.1340    0.0041    0.0009    0.0015    0.0173    0.0010    0.0034    0.0288
      ⋮

YTest = scores2label(scores,classNames);

真のテストラベル YTest および予測ラベル YPredicted の混同行列をプロットします。

plotconfusion(YTest,YTest)

行は予測されたクラス (出力クラス) に対応し、列は真のクラス (ターゲットクラス) に対応します。対角線上のセルは、正しく分類された観測値に対応します。対角線外のセルは、誤分類された観測値に対応します。観測値の数と観測値の総数に対する割合の両方が各セルに表示されます。

すべての Figure を閉じます。

close(findall(groot,'Type','figure'))

one-of-N ラベルを使用した混同行列のプロット

ライブスクリプトを開く

関数 cancer_dataset を使用してサンプルデータを読み込みます。XTrain は、699 個の生検データの 9 個の属性を定義する 9 行 699 列の行列です。YTrain は 2 行 699 列の行列で、各列は対応する観測値の正しいカテゴリを示します。YTrain の各列には 1 番目または 2 番目の行に 1 に等しい要素が 1 つあり、それぞれは良性または悪性の癌に対応しています。このデータセットの詳細を表示するには、コマンドラインで help cancer_dataset と入力します。

rng default
[XTrain,YTrain] = cancer_dataset;
YTrain(:,1:10)

ans = 2×10

     1     1     1     0     1     1     0     0     0     1
     0     0     0     1     0     0     1     1     1     0

パターン認識ネットワークを作成し、サンプルデータを使用して学習させます。

net = patternnet(10);
net = train(net,XTrain,YTrain);

学習済みネットワークを使用して癌の状態を推定します。行列 YPredicted の各列には、それぞれクラス 1 とクラス 2 に属している各観測値の予測確率が含まれています。

YPredicted = net(XTrain);
YPredicted(:,1:10)

ans = 2×10

    0.9980    0.9979    0.9894    0.0578    0.9614    0.9960    0.0026    0.0023    0.0084    0.9944
    0.0020    0.0021    0.0106    0.9422    0.0386    0.0040    0.9974    0.9977    0.9916    0.0056

混同行列をプロットします。プロットを作成するために、plotconfusion で最も高いクラス確率に従って各観測値にラベルを付けます。

plotconfusion(YTrain,YPredicted)

この図では、最初の 2 つの対角線上のセルが、学習済みネットワークによる正しい分類の数および比率を示します。たとえば、446 個の生検データが良性に正しく分類されているとします。これは 699 個のすべての生検データの 63.8% に相当します。同様に、236 個のケースが悪性に正しく分類されています。これはすべての生検データの 33.8% に相当します。

悪性の生検データのうち 5 個が誤って良性に分類されており、これはデータに含まれる 699 個のすべての生検データの 0.7% に相当します。同様に、良性の生検データのうち 12 個が誤って悪性に分類されており、これはデータ全体の 1.7% に相当します。

451 個の良性予測のうち、98.9% が正しく、1.1% が誤りです。248 個の悪性予測のうち、95.2% が正しく、4.8% が誤りです。458 個の良性ケースのうち、97.4% が正しく良性と予測されており、2.6% が悪性と予測されています。241 個の悪性ケースのうち、97.9% が正しく悪性に分類されており、2.1% が良性に分類されています。

全体では、予測の 97.6% が正しく、2.4% が誤っています。

入力引数

すべて折りたたむ

`targets` — 真のクラスラベル
categorical ベクトル | 行列

真のクラスラベル。次のいずれかに指定します。

categorical ベクトル。各要素は 1 つの観測値のクラスラベルです。引数 outputs と targets の要素数は同じでなければなりません。categorical ベクトルが、基になるクラスを定義している場合、基になるクラスの一部に観測値がない場合でも、plotconfusion は、基になるクラスをすべて表示します。引数が順序 categorical ベクトルである場合、両方の引数が同じ基になるカテゴリを同じ順序で定義していなければなりません。
N 行 M 列の行列。N はクラスの数、M は観測値の数です。行列の各列は one-of-N (one-hot) 表現でなければなりません。ここで、1 である 1 つの要素は真のラベルを示し、他のすべての要素は 0 です。

`outputs` — 予測クラスラベル
categorical ベクトル | 行列

予測クラスラベル。次のいずれかに指定します。

categorical ベクトル。各要素は 1 つの観測値のクラスラベルです。引数 outputs と targets の要素数は同じでなければなりません。categorical ベクトルが、基になるクラスを定義している場合、基になるクラスの一部に観測値がない場合でも、plotconfusion は、基になるクラスをすべて表示します。引数が順序 categorical ベクトルである場合、両方の引数が同じ基になるカテゴリを同じ順序で定義していなければなりません。
N 行 M 列の行列。N はクラスの数、M は観測値の数です。行列の各列は one-of-N (one-hot) 表現にできます。これは、1 である 1 つの要素が予測ラベルを示す、つまり、合計が 1 になる確率の形式です。

`name` — 混同行列の名前
文字配列

混同行列の名前。文字配列として指定します。plotconfusion は、指定された name をプロットのタイトルの先頭に追加します。

データ型: char

バージョン履歴

R2008a で導入

参考

trainnet | trainingOptions | dlnetwork

plotconfusion

構文

説明

例

カテゴリカル ラベルを使用した混同行列のプロット