csape

端点条件を使用した 3 次スプライン内挿

構文

pp = csape(x,y)

pp = csape(x,y,conds)

pp = csape(x,[e1,y,e2],conds)

pp = csape({x1,...,xn},___)

説明

pp = csape(x,y) は、与えられたデータ (x,y) に対して 3 次スプライン内挿の pp 型を返します。関数は、データの各端点にラグランジュ端点条件を適用し、スプラインの端点の傾きを、各端点の最後の 4 つのデータ点を近似する 3 次多項式の傾きに一致させます。同じサイトのデータ値は平均化されます。

pp = csape(x,y,conds) は、conds で指定された端点条件を使用します。

pp = csape(x,[e1,y,e2],conds) は、conds で指定された端点条件を使用し、左右の端点条件にそれぞれ e1 および e2 の各値を使用します。

pp = csape({x1,...,xn},___) は、一変量メッシュの入力 x1,...,xn を使用して、グリッド データの 3 次スプライン内挿を返します。この場合、y は n+r 次元配列となります。ここで、r は各データ値の次元です。conds は n 個のエントリをもつ cell 配列で、n 個の変数のそれぞれに端点条件を提供します。場合によっては、端点条件に対して端点条件を指定しなければなりません。この構文は、これより前の構文の任意の引数で使用できます。

例

csape を使用した、カスタマイズされた端点条件の使用

関数 csape を使用して、カスタムの端点条件を実装できます。左の端点、$\mathit{e}=$x(1) に次の条件を適用するとします。

$$\lambda (s)\equiv aDs(e)+b{D}^{2}s(e)=c$$

ここで、$\mathit{a}$、$\mathit{b}$、および $\mathit{c}$ はスカラーです。3 次スプライン内挿 $\mathit{s}$ を $$s_1$$ (指定されたデータに対する、既定の端点条件を使用した 3 次スプライン内挿) および $$s_0$$ (ゼロ データに対する、いくつかの自明ではない端点条件を使用した 3 次スプライン内挿) の和として計算できます。

$$s=s_1+\frac{c-\lambda (s_1)}{\lambda (s_0)}{s}_0$$

$$s_0$$ に指定する端点条件は、最終的に目的とする端点条件 $$\lambda (s)$$ である必要はありません。

この例では、チタン テスト データを使用します。これは、データ近似に使用される標準のデータセットです。関数 titanium を使用してデータを読み込みます。

[x,y] = titanium;

$$\lambda (s)$$ の係数を定義します。

a = -2;
b = -1;
c = 0;

端点条件は、データセットの左の端点に適用されます。

e = x(1);

ここで、端点条件を適用せずに、データセットの 3 次スプライン内挿を計算します。

s1 = csape(x,y);

$$s_0$$ を計算するには、一連の自明ではない追加端点条件で、y と同じ長さのゼロ データを使用します。

yZero = zeros(1,length(y));

1 行 2 列の行列 conds は、固定するスプラインの微分を指定することで端点条件を設定します。この例では、データの左端に対してのみ端点条件を使用するため、conds を使用して左端の 1 階微分を固定します。右端では、関数自体の値を固定します。

conds = [1 0];

関数または微分が固定される値を指定するには、その値を、近似するデータセット (この場合、yZero) に追加値として追加します。最初の要素は左端の値を指定し、最後の要素は右端の値を指定します。

左端では、スプラインの 1 階微分を 1 の値に固定します。右端では、関数自体を 0 (yZero の最後の要素の元の値) に固定します。yZero の両端でこれらの端点条件値をそれぞれ連結し、csape を使用して、これらの端点条件値をもつデータを近似するスプラインを求めます。

s0 = csape(x,[1 yZero 0],conds);

前述の $\mathit{s}$ の式を使用して、そのデータから、完全に近似されたスプラインを計算します。これを行うには、スプライン $$s_0$$ および $$s_1$$ の 1 階微分および 2 階微分を使用して、$${\lambda }_0=\lambda (s_0)$$ および $${\lambda }_1=\lambda (s_1)$$ の値を計算します。

d1s1 = fnder(fnbrk(s1,1));
d2s1 = fnder(d1s1);
d1s0 = fnder(fnbrk(s0,1));
d2s0 = fnder(d1s0);

端点条件はデータの左端にのみ適用されるため、スプラインの 1 番目の多項式区分の微分を計算します。

lam1 = a*fnval(d1s1, e) + b*fnval(d2s1,e);
lam0 = a*fnval(d1s0, e) + b*fnval(d2s0,e);

ここで、$${\lambda }_1$$ および $${\lambda }_0$$ を使用して最終的な、完全に近似されたスプラインを計算します。

pp = fncmb(s0,(c-lam1)/lam0,s1);

既定の近似および端点条件の結果を比較するために、スプラインをプロットします。

fnplt(pp,[594, 632])
hold on
fnplt(s1,'b--',[594, 632])
plot(x,y,'ro','MarkerFaceColor','r')
hold off
axis([594, 632, 0.62, 0.655])
legend 'Desired end conditions' ...
'Default end-conditions' 'Data' ...
    Location SouthEast

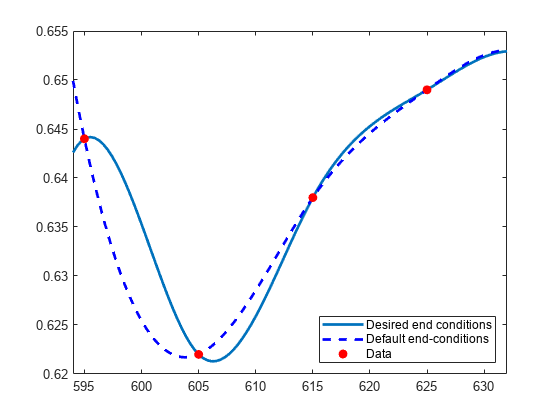
最初のデータ点付近の定留点は、近似において端点条件が実装されていることを示しています。

多変量データの近似

csape を使用して、多変量のベクトル値データに当てはめます。この例では、各独立変数に対して異なる端点条件を使用して、ベクトル値データに当てはめます。

まず、データを定義します。この例では、x 方向に固定条件、すなわち所定の傾き、y 方向に周期的な端点条件を使用して、2 次元フィールドに対する 3 次元のベクトル v を定義します。

x = 0:4;
y = -2:2;

s2 = 1/sqrt(2);

v = zeros( 3, 7, 5 );
v(1,:,:) = [1 0 s2 1 s2 0 -1].'*[1 0 -1 0 1];
v(2,:,:) = [1 0 s2 1 s2 0 -1].'*[0 1 0 -1 0];
v(3,:,:) = [0 1 s2 0 -s2 -1 0].'*[1 1 1 1 1];

v は、ベクトル値が座標 x(i),y(j) である 3 次元配列 v(:,i+1,j) です。x 次元の 2 つの追加エントリは傾きの値を指定します。データ点 v(:,1,j) および v(:,7,j) は、固定された端点条件に対し、線 x = 0 および x = 4 に沿った 1 階微分の値を提供します。y 次元では、周期的な端点条件にさらに指定する必要があるものはありません。

ここで、csape を使用して多変量の 3 次スプライン内挿を計算します。

sph = csape({x,y},v,{'clamped','periodic'});

結果をプロットするにはまず、適切な区間にわたってスプラインを評価します。

values = fnval(sph,{0:.1:4,-2:.1:2});

surf(squeeze(values(1,:,:)), ...
squeeze(values(2,:,:)), squeeze(values(3,:,:)));

axis equal
axis off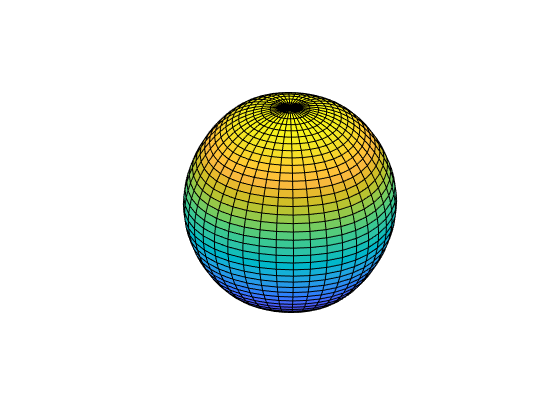

単純なコマンド fnplt(sph) を使用してスプライン曲面を評価およびプロットすることもできます。v は 3 次元配列であり、v(:,i+1,j) は (x(i),y(j))、i=1:5、j=1:5 で一致する 3 次元ベクトルであることに注意してください。また、conds{1} が 'clamped' であることから、size(v,2) は 7 (5 ではない) であり、v(r,:,j)の最初と最後のエントリは端点の傾きの値を指定します。

端点条件に対する端点条件の指定

場合によっては、端点条件の端点条件を指定しなければなりません。この二変量の例では、双三次内挿を完了することで、双三次多項式 g(x,y) = x³y³ を再現します。次に、端点条件値をどのように配置しなければならないのかを確認しやすくするために、端点条件値を含む必要なデータを直接 g から導出します。最後に、結果を確認します。

sites = {[0 1],[0 2]}; coefs = zeros(4, 4); coefs(1,1) = 1;
g = ppmak(sites,coefs);
Dxg = fnval(fnder(g,[1 0]),sites);
Dyg = fnval(fnder(g,[0 1]),sites);
Dxyg = fnval(fnder(g,[1 1]),sites);

f = csape(sites,[Dxyg(1,1),   Dxg(1,:),    Dxyg(1,2); ...
                 Dyg(:,1), fnval(g,sites), Dyg(:,2) ; ...
                 Dxyg(2,1),   Dxg(2,:),    Dxyg(2,2)], ...
                                          {'complete','complete'});
if any(squeeze(fnbrk(f,'c'))-coefs)
    disp( 'this is wrong' )
end

入力引数

x — データ サイト

ベクトル | cell 配列

近似対象のデータ値 y のデータ サイト。ベクトル、または多変量データの場合は cell 配列として指定します。関数は、すべての j について s(x(j)) = y(:,j) を満たすよう、各データ サイト x にスプライン s のノットを作成します。

多変量グリッド データの場合、x を、s(x1(i),x2(j),...,xn(k)) = y(:,i,j,...,k) を満たすような、各変数の次元のデータ サイトを提供する cell 配列として指定します。

データ型: single | double

y — 近似対象のデータ値

ベクトル | 行列 | 配列

スプライン作成時の近似対象のデータ値。ベクトル、行列、または配列として指定します。データ値 y(:,j) は、スカラー、行列、または n 次元配列として指定できます。同じデータ サイト x のデータ値は平均化されます。

データ型: single | double

conds — 端点条件

'clamped' | 'complete' | 'not-a-knot' | 'periodic' | 'second' | 'variational' | 1 行 2 列の行列

スプラインの端点条件。'complete'、'clamped'、'not-a-knot'、'periodic'、'second'、'variational'、または 1 行 2 列の行列として指定します。conds の事前定義のオプションは、データの各端点に同一の端点条件を適用します。conds を 1 行 2 列の行列として指定することで、各端点に異なる端点条件を指定することもできます。

使用できる事前定義された端点条件を次に示します。

'complete' または 'clamped'	端点の傾きが、指定された値 e1 および e2 と一致する。e1 および e2 を指定しない場合、このオプションでは、既定のラグランジュ端点条件と一致します。
'not-a-knot'	2 番目および最後から 2 番目のサイトが非アクティブなノットになる。このオプションでは、e1 および e2 に指定されたすべての値は無視されます。
'periodic'	左端の 1 階微分と 2 階微分が右端のそれぞれと一致する。
'second'	端点の 2 階微分が、指定された値 e1 および e2 と一致する。値 e1 および e2 を指定しない場合、このオプションでは、両方に対して既定値 0 を使用します。既定値を使用した場合、このオプションは 'variational' と同じになります。
'variational'	端点の 2 階微分が 0 に設定される。このオプションでは、e1 および e2 に指定されたすべての値は無視されます。

各端点に異なる端点条件を指定するには、conds を 1 行 2 列の行列として指定します。この行列の要素は、端点条件によって固定されるスプラインの微分の次数を指定します。conds(j) = i と設定した場合、i 階微分 Dⁱs は端点条件値に固定されます。

既定の端点条件値は、conds(1) = 1 の場合は、左側の 4 つのサイトで 3 次内挿の微分となります。それ以外の場合は 0 となります。データの左側および右側の端点条件値を、それぞれ e1 および e2 を指定して設定します。

conds(j) の値は 0、1、または 2 として指定できます。別の値を指定するか、または conds(j) を指定しない場合は、conds(j) が 1 となり、対応する端点条件値は既定値となります。

次の事前定義された端点条件を使用できます。

固定	Ds(e) = ej	if conds(j) == 1
曲線	D2s(e) = ej	if conds(j) == 2
周期的	Drs(a) = Drs(b), r = 1,2	if conds == [0 0]
変分	D2s(e) = 0	if conds(j) == 2 & ej == 0

e、a、および b は、左または右のデータ位置を表します。ej は、データの左端では e1、データの右端では e2 となります。

conds の事前定義オプションとユーザー定義オプションのどちらを使用する場合でも、オプションの端点条件値 e1 および e2 を指定できます。ただし、conds の一部の事前定義オプションは、指定した任意の端点条件値を無視することに注意してください。

例: 'clamped', [1 0]

e1 — 左の端点条件値

スカラー

スプラインの左の端点条件値。スカラー値として指定します。e1 は、データの左端の i 階微分の値を指定します。ここで、i は conds によって提供されます。両端点で異なる端点条件を使用している場合でも、1 つの端点に端点条件値を指定する場合は、もう 1 つの端点にも指定しなければなりません。

conds の一部の事前定義オプションは、指定した任意の端点条件値を無視することに注意してください。

e1 の既定値は、conds(1) = 1 の場合は、左側の 4 つのサイトで 3 次内挿の微分となります。それ以外の場合は 0 となります。

データ型: single | double

e2 — 右の端点条件値

スカラー

スプラインの右の端点条件値。スカラー値として指定します。e2 は、データの右端の i 階微分を指定します。ここで、i は conds によって提供されます。両端点で異なる端点条件を使用している場合でも、1 つの端点に端点条件値を指定する場合は、もう 1 つの端点にも指定しなければなりません。

conds の一部の事前定義オプションは、指定した任意の端点条件値を無視することに注意してください。

e2 の既定値は、conds(2) = 1 の場合は、右側の 4 つのサイトで 3 次内挿の微分となります。それ以外の場合は 0 となります。

データ型: single | double

出力引数

pp — pp 型のスプライン

スプラインの構造体

pp 型のスプライン。次のフィールドがある構造体として返されます。

Form — スプラインの形式

pp

スプラインの形式。pp として返されます。pp は、スプラインが区分的多項式型であることを示します。

Breaks — スプラインのノットの位置

ベクトル | cell 配列

スプラインのノットの位置。ベクトル、または多変量データの場合はベクトルの cell 配列として返されます。ベクトルには厳密に増加する要素が含まれます。これらの要素は、多項式区分が定義される各区間の開始と終了を表します。

Coefs — 多項式の係数

行列 | 配列

各区分の多項式の係数。行列、または多変量データの場合は配列として返されます。

Pieces — 多項式区分の数

スカラー | ベクトル

スプラインを記述する多項式区分の数。スカラー、または多変量データの場合は各変数の区分数のベクトルとして返されます。

Order — 多項式の次数

スカラー | ベクトル

スプラインの各多項式区分を記述する多項式関数の次数。スカラー、または多変量データの場合は各変数の次数を含むベクトルとして返されます。

Dim — 次元

スカラー

ターゲット関数の次元。スカラーとして返されます。

アルゴリズム

関連する三重対角線形システムは MATLAB^® のスパース行列機能を使用して構成され、解決されます。

csape コマンドは、Fortran ルーチン CUBSPL の大きく展開されたバージョンを PGS に呼び出します。

バージョン履歴

R2006a より前に導入

参考

csapi | spapi | spline