Tune Feedback Loops Using looptune
This example shows the basic workflow of tuning feedback loops with the looptune command. looptune is similar to systune and meant to facilitate loop shaping design by automatically generating the tuning requirements.
Engine Speed Control
This example uses a simple engine speed control application as shown in the following figure. The control system consists of a single PID loop and the PID controller gains must be tuned to adequately respond to step changes in the desired speed. Specifically, you want the response to settle in less than 5 seconds with little or no overshoot.

Use the following fourth-order model of the engine dynamics.
load rctExamples Engine bode(Engine) grid

Specify Tunable Elements
You need to tune the four PID gains to achieve the desired performance. Use a tunablePID object to parameterize the PID controller.
PID0 = tunablePID('SpeedController','pid')
Tunable continuous-time PID controller "SpeedController" with formula:
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
and tunable parameters Kp, Ki, Kd, Tf.
Block Properties
Type "pid(PID0)" to see the current value.
Build Tunable Model of Feedback Loop
looptune tunes the generic SISO or MIMO feedback loop shown in the following figure. This feedback loop models the interaction between the plant and the controller. Note that this is a positive feedback interconnection.

For the speed control loop, the plant is the engine model and the controller consists of a PID controller and prefilter .

To use looptune, create models for and . Assign names to the inputs and outputs of each model to specify the feedback paths between plant and controller. Note that the controller has two inputs: the speed reference r and the speed measurement speed.
F = tf(10,[1 10]); % prefilter G = Engine; G.InputName = 'throttle'; G.OutputName = 'speed'; C0 = PID0 * [F , -1]; C0.InputName = {'r','speed'}; C0.OutputName = 'throttle';
Here, C0 is a generalized state-space model (genss) that depends on the tunable PID block PID0.
Tune Controller Parameters
You can now use looptune to tune the PID gains subject to a simple control bandwidth requirement. To achieve the 5-second settling time, the gain crossover frequency of the open-loop response should be approximately 1 rad/s. Given this basic requirement, looptune automatically shapes the open-loop response to provide integral action, high-frequency roll-off, and adequate stability margins. Note that you could specify additional requirements to further constrain the design. For an example, see Decoupling Controller for a Distillation Column.
wc = 1; % target gain crossover frequency
[~,C,~,Info] = looptune(G,C0,wc);Final: Peak gain = 0.976, Iterations = 7 Achieved target gain value TargetGain=1.
The final value is less than 1, indicating that the desired bandwidth was achieved with adequate roll-off and stability margins. looptune returns the tuned controller C. Use getBlockValue to retrieve the tuned value of the PID block.
PIDT = getBlockValue(C,'SpeedController')PIDT =
1 s
Kp + Ki * --- + Kd * --------
s Tf*s+1
with Kp = 0.00148, Ki = 0.00259, Kd = -0.00089, Tf = 1.19
Name: SpeedController
Continuous-time PIDF controller in parallel form.
Model Properties
Validate Results
Use loopview to validate the design and visualize the loop shaping requirements implicitly enforced by looptune.
clf loopview(G,C,Info)
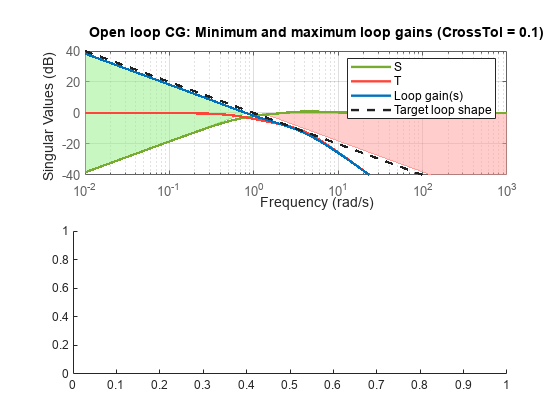
Next, plot the closed-loop response to a step command in engine speed. The tuned response satisfies the requirements.
T = connect(G,C,'r','speed'); % closed-loop transfer function from r to speed clf step(T)
