拡張カルマンフィルターを使用したラップされた測定値による状態推定

この例では次を使用します。

Simulink Simulink

この例では、循環的にラップされる角度測定値を伴う 3 次元追従用の非線形の状態推定に拡張カルマンフィルターアルゴリズムを使用する方法を示します。通常、ターゲット追従用のセンサーは、球面座標系を使用してオブジェクトの位置を方位角、範囲、および仰角で報告します。このセットからの角度測定値は一定の範囲内で報告されます。たとえば、方位角は $- 18 0^{\circ}$ ～ $18 0^{\circ}$ または $0^{\circ}$ ～ $36 0^{\circ}$ の範囲で報告されます。ただし、追従は一般に矩形座標系で行われるため、球面座標系の測定を矩形座標系の状態に変換するために必要な非線形変換を処理できる非線形フィルターの使用が必要になります。

この例では、等速モデルを使用して、ターゲットの 3 次元の位置と速度を追従します。このオブジェクトの状態を追従するための非線形フィルターとして拡張カルマンフィルターを使用しています。このフィルターでは、この追従の演習においては、方位角 ( $ψ$ )、範囲、および仰角 ( $ϕ$ ) の読み取り値を測定値として使用します。

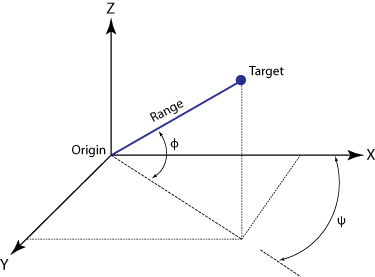
この例の等速 3 次元プラントモデルは、次に示す 3 つの軸の位置と速度で構成されています。

$S t a t e s = [\begin{array}{c} x \\ x_{}^{˙} \\ y \\ y_{}^{˙} \\ z \\ z_{}^{˙} \end{array}] = [\begin{array}{c} x \\ v_{x} \\ y \\ v_{y} \\ z \\ v_{z} \end{array}]$

範囲、方位角、仰角は次によって与えられます。

$\begin{array}{l} R a n g e = \sqrt{x^{2} + y^{2} + z^{2}} \\ E l e v a t i o n (ϕ) = \sin^{- 1} (\frac{z}{R a n g e}) \\ A z i m u t h (ψ) = \tan^{- 1} (\frac{y}{x}) \end{array}$

フィルター処理のプロセスでは、実際の測定値と想定される測定値の残差を計算する手順が欠かせません。必要な対策を講じておかないと、ラップの境界の近くにあるオブジェクトで残差値が大きくなることがあります。これは、フィルターが正確な状態から離れ、状態推定が不正確になる原因となります。この例では、そのような状況に測定値のラップを使用して対処する方法を示します。測定値のラップを使用する場合と使用しない場合の追従される状態の差を Simulink® モデルを使用して示しています。

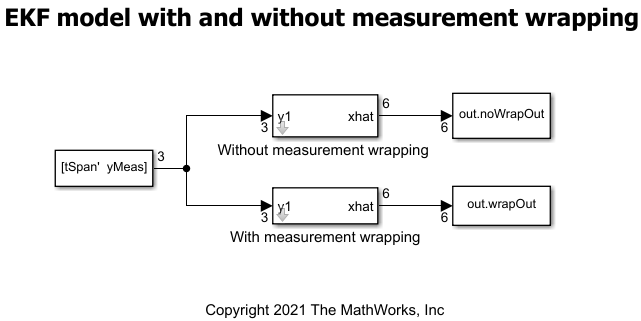
状態推定 - 測定値のラップなし

最初に、初期状態推定を与え、モデル名を指定します。

rng(0)
initialStateGuess = [-100 0 0 0 0 0]';
modelName = 'modelEKFWrappedMeasurements';

ノイズ共分散に基づく測定値を次のように生成します。

dt = 3;
tSpan = 0:dt:100;
yTrue = zeros(length(tSpan),3);
yMeas = zeros(size(yTrue));
noiseCovariance = diag([20 0.5 0.5]);
xCurrent = initialStateGuess;

for i = 1:numel(tSpan)
   xTrue = stateTransitionFcn(xCurrent);
   yTrue(i,:) = (measurementFcn(xTrue))';
   yMeas(i,:) = yTrue(i,:) + (chol(noiseCovariance)*randn(3,1))';
   xCurrent = xTrue;
end

モデルのシミュレーションを実行します。

out = sim(modelName);
xEstNoWrap = zeros(numel(tSpan),length(initialStateGuess));
xEstWithWrap = zeros(numel(tSpan),length(initialStateGuess));

フィルターを実行し、3 次元プロットで状態の収束を可視化します。

figure()
plot3(initialStateGuess(1), initialStateGuess(3), initialStateGuess(5),'ro','MarkerFaceColor','r','MarkerSize',9);
grid
hold on;

% Plot options
xlabel('x');
ylabel('y');
zlabel('z');
title('No measurement wrapping');

% Run filter
for i = 1:numel(tSpan)
   xEst = out.noWrapOut(i,:);
   plot3(xEst(1),xEst(3),xEst(5),'bo','MarkerFaceColor','b');   
   hold on;
   xEstNoWrap(i,:) = xEst;
end
hold off

状態推定 - 測定値のラップあり

次に、測定値のラップを有効にし、フィルターを実行します。3 次元プロットで状態の収束を可視化します。

figure()
% Run filter
for i = 1:numel(tSpan)
   xEst = out.wrapOut(i,:);
   plot3(xEst(1),xEst(3),xEst(5),'bo','MarkerFaceColor','b');   
   hold on;
   xEstWithWrap(i,:) = xEst;
end
plot3(initialStateGuess(1), initialStateGuess(3), initialStateGuess(5),'ro','MarkerFaceColor','r','MarkerSize',9);
grid
title('With measurement wrapping');
hold off

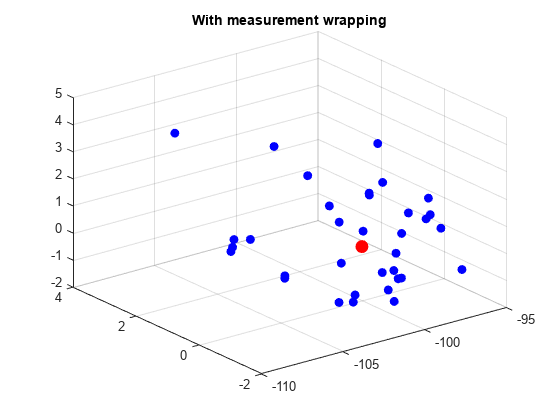
上記のプロットから、測定値のラップなしの 3 次元プロットに比べて、3 つの軸のスケールが大幅に小さくなっていることがわかります。これは、測定値のラップを有効にした場合の方が適切に収束することを示しています。

検証

両方の場合の推定誤差を同じプロットで比較します。

figure()
subplot(3,1,1)
plot(xEstNoWrap(:,1) - xTrue(1));
hold on
plot(xEstWithWrap(:,1) - xTrue(1));
ylim([-500 1200])
title('e_x');
hold off

subplot(3,1,2)
plot(xEstNoWrap(:,3) - xTrue(3));
hold on
plot(xEstWithWrap(:,3) - xTrue(3));
ylim([-2000 1000])
hold off
title('e_y');

subplot(3,1,3)
plot(xEstNoWrap(:,5) - xTrue(5));
hold on
plot(xEstWithWrap(:,5) - xTrue(5));
ylim([-200 200])
hold off
title('e_z');

sgtitle('Estimation Error Plot')
legend('No Wrapping', 'With Wrapping','location','best')

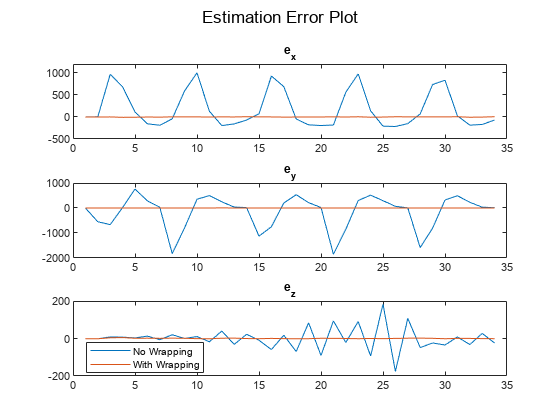
この比較から、3 つのすべての軸について、測定値のラップなしの場合の方が誤差がはるかに大きくなっていることがわかります。

まとめ

この例では、非線形システムの状態推定に Extended Kalman Filter ブロックを使用する方法について、測定値のラップを使用する場合と使用しない場合の例を示しています。3 次元プロットと誤差プロットからわかるように、ラップを有効にした状態推定の方が正確な状態推定が得られます。

サポート関数

状態遷移関数

Extended Kalman Filter ブロックには、タイムステップ間の状態の変化を記述する関数が必要です。これは一般に状態遷移関数と呼ばれます。この例の stateTransitionFcn.m に含まれている状態遷移関数の内容は次のとおりです。

function x = stateTransitionFcn(x)
   dt = 3;
   A = [1 dt 0 0  0 0;
        0 1  0 0  0 0;
        0 0  1 dt 0 0;
        0 0  0 1  0 0;
        0 0  0 0  1 dt;
        0 0  0 0  0  1];
   x = A*x;
end

測定関数

Extended Kalman Filter ブロックには、モデルの状態とセンサーの測定値の関係を記述する関数も必要です。これは測定関数です。この例の measurementFcn.m に含まれている測定関数の内容は次のとおりです。

function [y, bounds] = measurementFcn(x)
   xPos = x(1);
   yPos = x(3);
   zPos = x(5);

   % Range
   r = sqrt(xPos^2 + yPos^2 + zPos^2);
   % Azimuth
   psi = atan2d(yPos,xPos);
   % Elevation
   phi = asind(zPos/r);
   % Combined measurement
   y = [r ; psi; phi];
   bounds = [-inf inf;-180 180; -90 90]; 
end

参考

Extended Kalman Filter

拡張カルマン フィルターを使用したラップされた測定値による状態推定