システム応答のプロット

ライブ スクリプトを開く

この例では、SISO および MIMO 線形システムの時間応答と周波数応答をプロットする方法を示します。

時間応答

線形システムを作成します。この例では、3 次伝達関数を作成します。

sys = tf([8 18 32],[1 6 14 24])
sys =
 
     8 s^2 + 18 s + 32
  -----------------------
  s^3 + 6 s^2 + 14 s + 24
 
Continuous-time transfer function.
Model Properties

このシステムのステップ応答とインパルス応答をプロットするには、step コマンドと impulse コマンドを使用します。

subplot(2,1,1)
step(sys)
subplot(2,1,2)
impulse(sys)

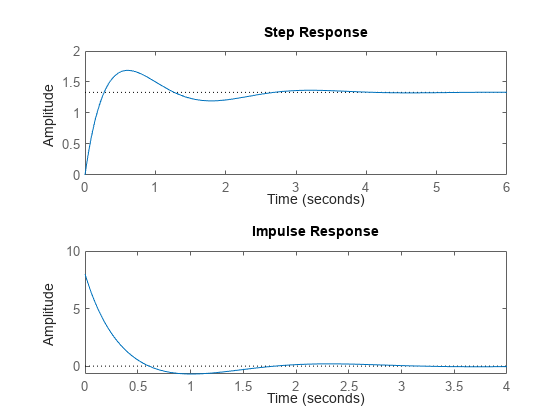
MATLAB figure

lsim コマンドを使用すると、任意の信号 (正弦波など) に対する応答をシミュレートすることもできます。入力信号は灰色、システム応答は青色で表示されます。

figure
t = 0:0.01:4;
u = sin(10*t);
lsim(sys,u,t)   % u,t define the input signal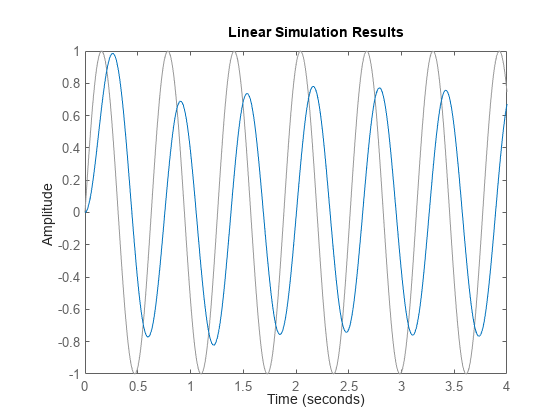

MATLAB figure

連続または離散の tf モデル、ss モデル、または zpk モデルでは、プロット コマンドを使用できます。状態空間モデルの場合は、特定の初期状態からの強制のない応答をプロットすることもできます。以下に例を示します。

A = [-0.8 3.6 -2.1;-3 -1.2 4.8;3 -4.3 -1.1];
B = [0; -1.1; -0.2];
C = [1.2 0 0.6];
D = -0.6;
G = ss(A,B,C,D);
x0 = [-1;0;2];  % initial state
initial(G,x0)
grid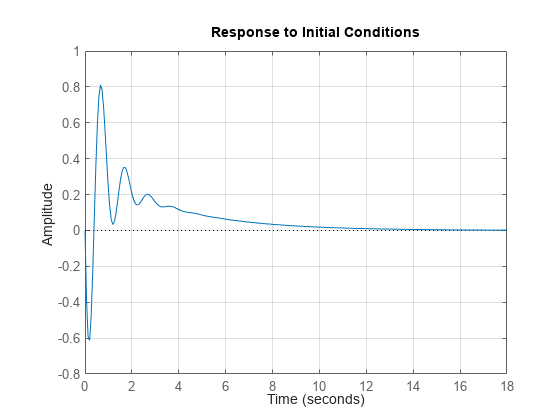

MATLAB figure

周波数応答

周波数領域解析は、制御システムの安定性と性能に関するプロパティを理解するうえで重要となります。ボード線図、ナイキスト線図、およびニコルス線図は、線形システムの周波数応答をプロットし、解析するための標準的な方法の 3 つです。これらのプロットを作成するには、bode、nichols、nyquist の各コマンドを使用します。

線形システムを作成します。

sys = tf([8 18 32],[1 6 14 24])
sys =
 
     8 s^2 + 18 s + 32
  -----------------------
  s^3 + 6 s^2 + 14 s + 24
 
Continuous-time transfer function.
Model Properties

このシステムのボード線図を作成します。

bode(sys)
grid

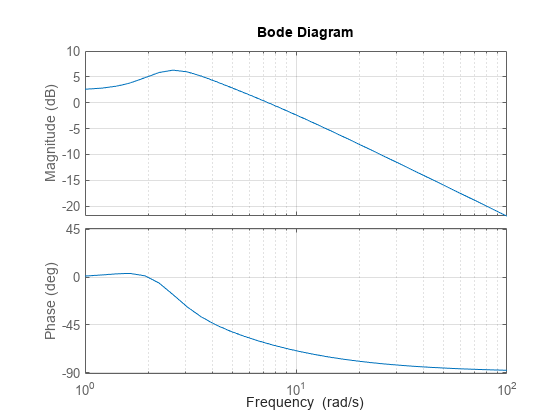
MATLAB figure

このシステムのナイキスト線図を作成します。

nyquist(sys)
grid

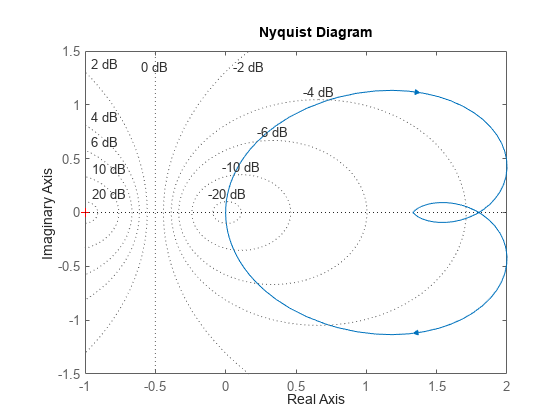
MATLAB figure

このシステムのニコルス線図を作成します。

nichols(sys)
grid

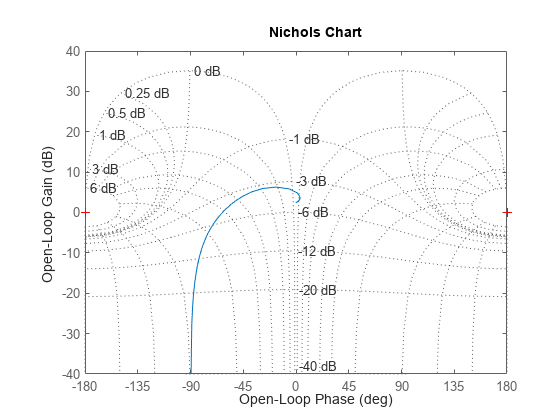
MATLAB figure

極/零点配置図と根軌跡

システムの極と零点には、そのシステムのダイナミクス、安定性、および性能制約に関する貴重な情報が含まれています。たとえば、次の SISO 制御ループのフィードバック ループについて考えます。

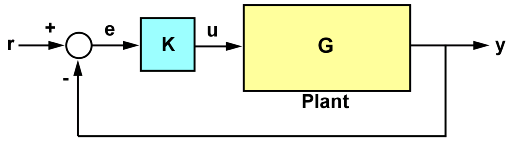
ここで、以下となります。

G=-(2s+1)s2+3s+2

ゲイン値 k = 0.7 に対し、pzmap を使用して閉ループの極と零点をプロットできます。

s = tf('s');
G = -(2*s+1)/(s^2+3*s+2);
k = 0.7;
T = feedback(G*k,1);
pzmap(T)
grid
axis([-2 0 -1 1])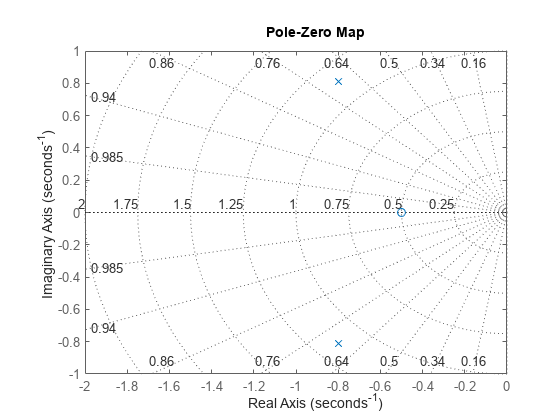

MATLAB figure

閉ループ極 (青い x でマーク) は左半平面にあるため、ゲイン k にこの値を選択すると、フィードバック ループは安定します。この図からは、閉ループ極の減衰率を読み取ることができます (放射線上のラベルを参照)。ここでは、減衰率が約 0.7 になっており、次のコマンドによって確認できるとおり、閉ループ応答が大きく減衰していることが示されています。

figure
step(T)

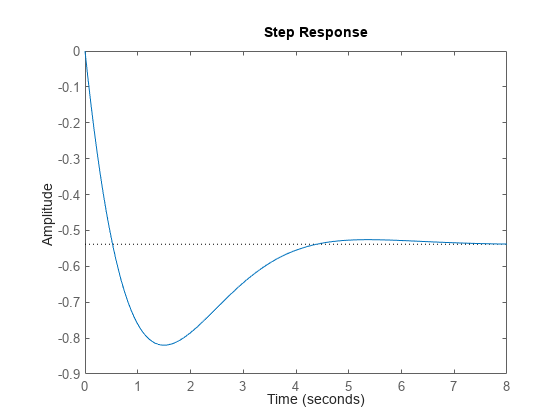
MATLAB figure

ループ ゲイン k が閉ループの安定性に与える影響を詳しく理解するには、閉ループ極の軌跡を k の関数としてプロットします。

rlocus(G)
grid

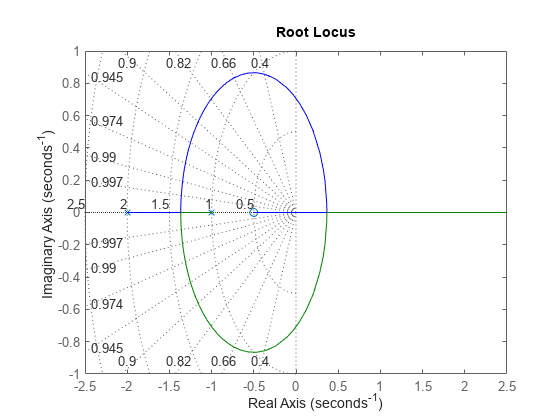
MATLAB figure

軌跡が y 軸と交差する箇所をクリックすると、閉ループ極が k = 1.51 の場合に不安定になることがわかります。そのため、閉ループの安定性を保つには、ループ ゲインを 1.5 より低く維持する必要があります。

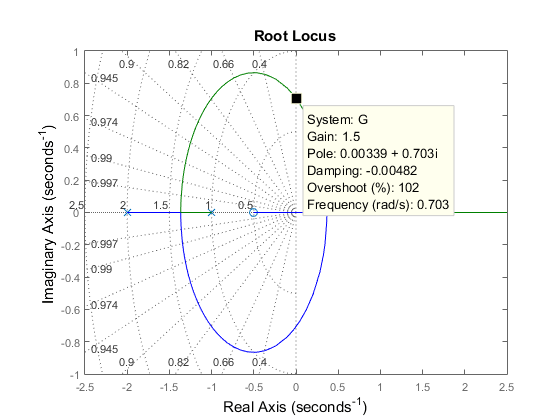
応答の特性

応答プロットを右クリックすると、さまざまなオプションや注釈にアクセスできます。たとえば、[特性] メニューを使用すると、ステップ応答の立ち上がり時間と整定時間、周波数応答プロットのピーク ゲインと安定余裕などの標準的なメトリクスを表示できます。

前の節と同じ例を使用して、閉ループ ステップ応答をプロットします。

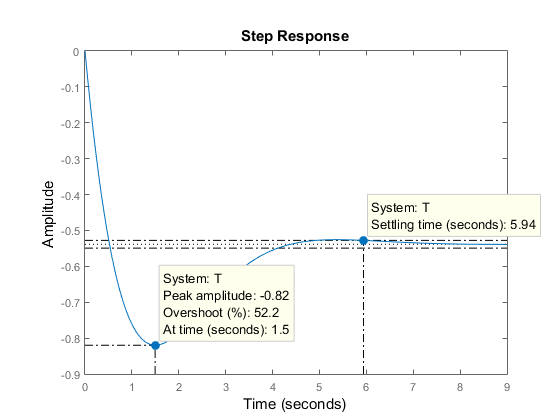
step(T)

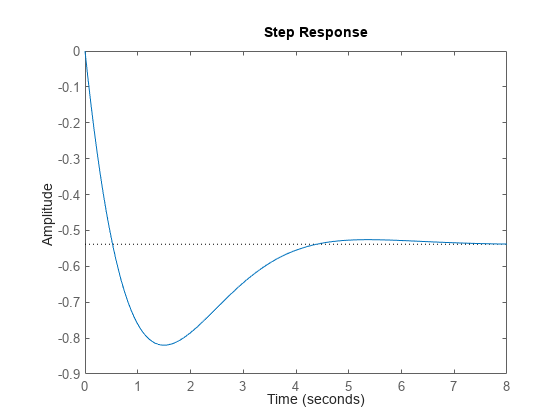
MATLAB figure

次に、プロットを右クリックしてピーク応答と整定時間の各特性を表示し、青いドットをクリックして、それに対応するオーバーシュート値と整定時間値を読み取ります。

MIMO システムの解析

ここまでに取り上げたコマンドはすべて、多入力多出力 (MIMO) システムを完全にサポートしています。MIMO では、これらのコマンドによってプロットの配列が生成されます。たとえば、次の 2 入力 2 出力のシステムについて考えます。

sys = rss(3,2,2);
sys.A = [-0.5 -0.3 -0.2 ; 0 -1.3  -1.7; 0.4 1.7 -1.3];

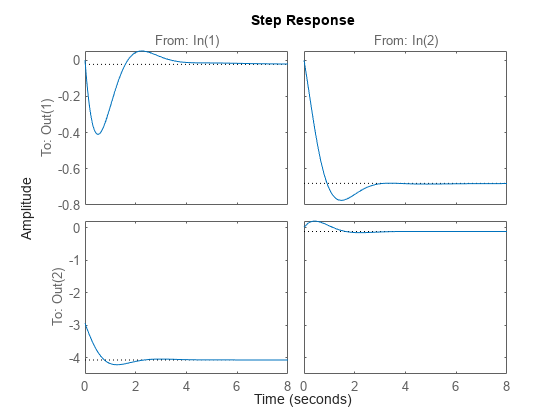
ステップ応答は 2 行 2 列のプロット配列となり、各列に特定の入力チャネルのステップ応答が示されます。

step(sys)

MATLAB figure

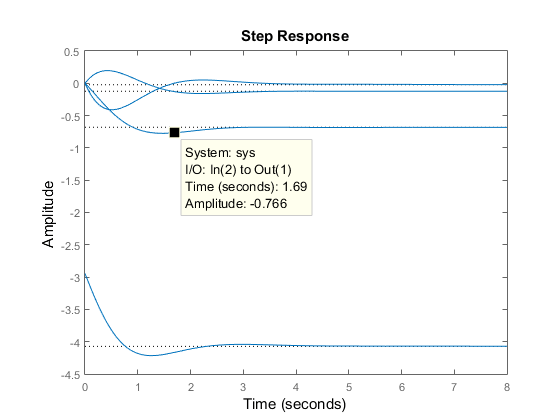
プロットを右クリックして、[I/O のグループ化]、[すべて] サブメニューを選択することによって、4 つの応答すべてを単一のプロットにグループ化できます。

MIMO システムを解析する場合に便利な追加のプロットは以下のとおりです。

  • 周波数応答の主ゲインを示す特異値プロット (sigma)

  • 各 I/O ペアに対する極/零点配置図 (iopzplot)

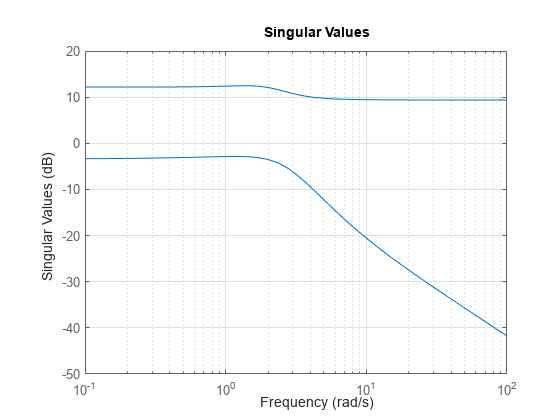
たとえば、sys のピーク ゲインを周波数の関数としてプロットします。

sigma(sys)
grid

MATLAB figure

システムの比較

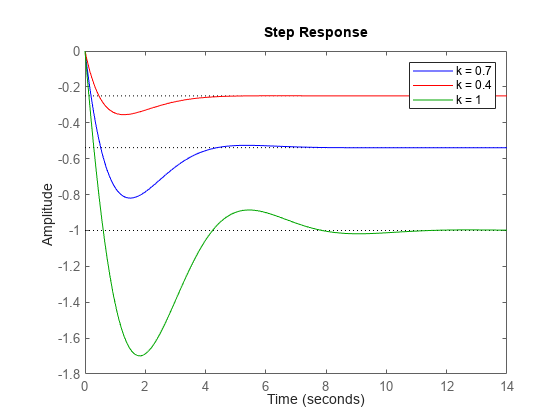
応答プロット コマンドを使用すると、一度に複数のシステムをプロットできます。特定の色、マーカー、またはライン スタイルを各システムに割り当てて、比較しやすくすることもできます。上記のフィードバック例を使用して、ループ ゲイン k の 3 つの値に対する閉ループ ステップ応答を 3 色でプロットします。

k1 = 0.4;
T1 = feedback(G*k1,1);
k2 = 1;
T2 = feedback(G*k2,1);
step(T,'b',T1,'r',T2,'g')
legend('k = 0.7','k = 0.4','k = 1');

MATLAB figure

時間軸または周波数軸の値の変更

既存の線形解析プロットの時間ベクトルまたは周波数ベクトルを変更できます。

step および impulse のプロットについては、プロット領域を右クリックして [時間の指定] を選択し、時間ベクトルを指定できます。

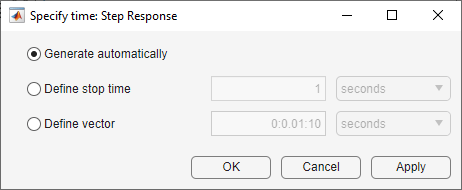
[時間の指定] ダイアログ ボックスで、次のいずれかの方法を使用して時間の値と単位を定義できます。

  • 自動生成 — 時間ベクトルをシステム ダイナミクスに基づいて自動的に生成します。このオプションはスパース システムに対してはサポートされません。

  • 終了時間の定義 — 終了時間を指定します。時間 0 から始まる時間ベクトルが作成されます。時間ベクトルのステップ サイズはシステム ダイナミクスに基づいて決定されます。

  • ベクトルの定義 — プロットする時間を等間隔の単調増加する時間値のベクトルとして指定します。

bode、nyquist、nichols、および sigma のプロットについては、プロット領域を右クリックして [周波数の指定] を選択し、周波数ベクトルを指定できます。

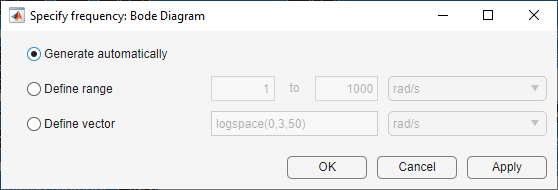
[周波数の指定] ダイアログ ボックスで、次のいずれかの方法を使用して周波数の値と単位を定義できます。

  • 自動生成 — 周波数ベクトルをシステム ダイナミクスに基づいて自動的に生成します。この方法はスパース システムに対してはサポートされません。

  • 範囲の定義 — 周波数範囲を指定します。この方法はスパース システムに対してはサポートされません。

  • ベクトルの定義 — プロットする周波数をベクトルとして指定します。

システムが frd オブジェクトの場合、プロットの周波数値の間に応答が内挿されます。

時間および周波数の単位を変更したときに指定されるのは入力の単位であり、プロット内の単位は変更されません。

参考

|

トピック