MIMO 状態空間モデル

陽的な MIMO 状態空間モデル

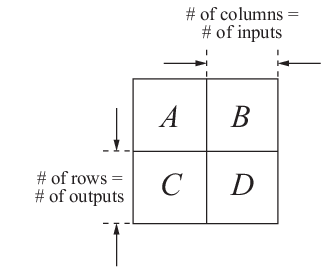
MIMO 状態空間モデルは、SISO 状態空間モデルを作成するのと同じ方法で作成します。SISO の場合と MIMO の場合の唯一の相違点は、状態空間行列の次元です。行列 B、C、および D の次元は、次の図に示すように入力と出力の数とともに増加します。

この例では、慣性テンソル J、減衰力 F、および回転の 3 軸を次のように関連させて、回転体の状態空間モデルを作成します。

$\begin{matrix} J \frac{d ω}{d t} + F ω = T \\ y = ω . \end{matrix}$

システム入力 T は駆動トルクです。出力 y は回転体の角速度のベクトルです。

このシステムを状態空間形式で表すには、

$\begin{matrix} \frac{d x}{d t} = A x + B u \\ y = C x + D u \end{matrix}$

次のように書き直します。

$\begin{matrix} \frac{d ω}{d t} = - J^{- 1} F ω + J^{- 1} T \\ y = ω . \end{matrix}$

すると、状態空間行列は次のようになります。

$A = - J^{- 1} F, B = J^{- 1}, C = I, D = 0.$

このモデルを作成するには、次のコマンドを入力します。

J = [8 -3 -3; -3 8 -3; -3 -3 8];
F = 0.2*eye(3);
A = -J\F;
B = inv(J);
C = eye(3);
D = 0;
sys_mimo = ss(A,B,C,D);

これらのコマンドは、J が角を中心に回転する立方体の慣性テンソルであり、減衰力が振幅 0.2 であることを想定しています。

sys_mimo は ss モデルです。

MIMO 記述子状態空間モデル

この例は、dss を使用して連続時間記述子 (陰的な) 状態空間モデルを作成する方法を示します。

この例では、陽的な MIMO 状態空間モデルで示したものと同じ回転体システムを使用します。そこでは、慣性行列 J の逆行列を求めて行列 B の値を取得しました。J は逆行列を求めるための条件が悪い場合、代わりに記述子 (陰的な) 状態空間モデルを使用できます。"記述子 (陰的な) 状態空間モデル" は次の形式です。

$\begin{matrix} E \frac{d x}{d t} = A x + B u \\ y = C x + D u \end{matrix}$

慣性テンソル J、減衰力 F、および回転の 3 軸を次のように関連させて、回転体の状態空間モデルを作成します。

$\begin{matrix} J \frac{d ω}{d t} + F ω = T \\ y = ω . \end{matrix}$

システム入力 T は駆動トルクです。出力 y は回転体の角速度のベクトルです。このシステムを次の状態空間行列をもつ記述子状態空間モデルとして作成できます。

$A = - F, B = I, C = I, D = 0, E = J .$

このシステムを作成するには、次のように入力します。

J = [8 -3 -3; -3 8 -3; -3 -3 8];
F = 0.2*eye(3);
A = -F;
B = eye(3);
C = eye(3);
D = 0;
E = J;
sys_mimo = dss(A,B,C,D,E)

これらのコマンドは、J が角を中心に回転する立方体の慣性テンソルであり、減衰力が振幅 0.2 であることを想定しています。

sys は、空ではない E 行列のある ss モデルです。

ジェット機の状態空間モデル

この例は、ジェット輸送機の MIMO モデルの構築法を示します。ジェット機の物理モデルへの展開の説明は長くなりますので、ここでは、状態空間方程式のみ説明します。飛行機の巡航に関する物理的な背景の詳細に関しては、航空に関する参考文献を参照してください。

マッハ 0.8、高度 40,000 フィートで飛行中のジェットモデルは、次のように表せます。

A = [-0.0558   -0.9968    0.0802    0.0415
      0.5980   -0.1150   -0.0318         0
     -3.0500    0.3880   -0.4650         0
           0    0.0805    1.0000         0];

B = [ 0.0073         0
     -0.4750    0.0077
      0.1530    0.1430
           0         0];

C = [0     1     0     0
     0     0     0     1];

D = [0     0
     0     0];

次のコマンドを使用して、LTI オブジェクトとして、状態空間モデルを作成し、状態、入力、および出力に名前を付けます。

states = {'beta' 'yaw' 'roll' 'phi'};
inputs = {'rudder' 'aileron'};
outputs = {'yaw rate' 'bank angle'};

sys_mimo = ss(A,B,C,D,'statename',states,...
'inputname',inputs,...
'outputname',outputs);

「sys_mimo」と入力すると、LTI モデルを表示できます。

sys_mimo

 
a = 
                      beta          yaw         roll          phi
         beta      -0.0558      -0.9968       0.0802       0.0415
          yaw        0.598       -0.115      -0.0318            0
         roll        -3.05        0.388       -0.465            0
          phi            0       0.0805            1            0
 
 
b = 
                    rudder      aileron
         beta       0.0073            0
          yaw       -0.475       0.0077
         roll        0.153        0.143
          phi            0            0
 
 
c = 
                      beta          yaw         roll          phi
     yaw rate            0            1            0            0
   bank angle            0            0            0            1
 
 
d = 
                    rudder      aileron
     yaw rate            0            0
   bank angle            0            0
 
Continuous-time model.

モデルには、2 つの入力と 2 つの出力があります。単位は、beta (横すべり角) と phi (バンク角) に対してはラジアン、yaw (ヨーレート) と roll (ロールレート) に対してはラジアン/秒です。方向舵と補助翼の偏向角の単位も度です。

SISO の場合は、関数 tf を使用して、伝達関数表現を導出できます。

tf(sys_mimo)

 
Transfer function from input "rudder" to output...
               -0.475 s^3 - 0.2479 s^2 - 0.1187 s - 0.05633
 yaw rate:  ---------------------------------------------------
            s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
 
                         0.1148 s^2 - 0.2004 s - 1.373
 bank angle:  ---------------------------------------------------
              s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
 
Transfer function from input "aileron" to output...
            0.0077 s^3 - 0.0005372 s^2 + 0.008688 s + 0.004523
 yaw rate:  ---------------------------------------------------
            s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674
 
                        0.1436 s^2 + 0.02737 s + 0.1104
 bank angle:  ---------------------------------------------------
              s^4 + 0.6358 s^3 + 0.9389 s^2 + 0.5116 s + 0.003674

参考

ss