化学反応器プラントの内部モデルコントローラーの設計

ライブスクリプトを開く

この例では、"制御システムデザイナー" を使用して直列化学反応器に対して IMC 構造内に補償器を設計する方法について説明します。プロセス制御アプリケーションでは、モデルベースの制御システムを使用して設定値追従し、負荷外乱を抑制することがよくあります。

プラントモデル

この例のプラントは 2 つのよく混合されたタンクで構成される化学反応器システムです。

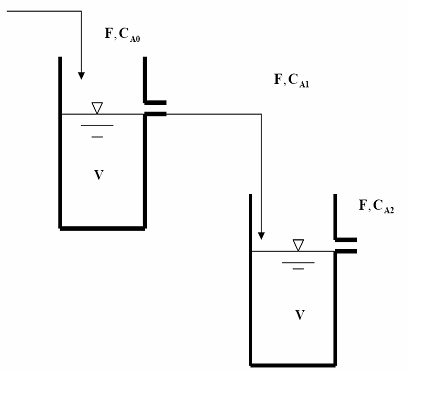
反応器では一定温度が保持されており、各反応器内の反応は成分 A について 1 次です。

$r_{A} = - k C_{A}$

システムには物質収支が適用され、システムに対して動的なモデルが生成されます。タンク内の水位はオーバーフローノズルによって一定に保たれているため、水位制御は行われません。

このプラントの詳細は、Example 3.3 in Chapter 3 of "Process Control: Design Processes and Control Systems for Dynamic Performance" by Thomas E. Marlin を参照してください。

次の微分方程式は成分の収支を記述します。

$V \frac{d C_{A 1}}{d t} = F (C_{A 0} - C_{A 1}) - V k C_{A 1}$

$V \frac{d C_{A 2}}{d t} = F (C_{A 1} - C_{A 2}) - V k C_{A 2}$

定常状態では、

$\frac{d C_{A 1}}{d t} = 0$

$\frac{d C_{A 2}}{d t} = 0$

その物質収支は次になります。

$F^{*} (C_{A 0}^{*} - C_{A 1}^{*}) - V k C_{A 1}^{*} = 0$

$F^{*} (C_{A 1}^{*} - C_{A 2}^{*}) - V k C_{A 2}^{*} = 0$

ここで、 $C_{A 0}^{*}$ 、 $C_{A 1} *$ 、および $C_{A 2} *$ は定常値です。

次の設計仕様と反応器のパラメーターを置換します。

$F^{*}$ = 0.085 $m o l e / m i n$
$C_{A 0}^{*}$ = 0.925 $m o l / m i n$
$V$ = 1.05 $m^{3}$
$k$ = 0.04 $m i n^{- 1}$

結果として 2 つの反応器内に次の定常状態濃度値が得られます。

$C_{A 1}^{*} = K C_{A 0}^{*} = 0.6191 m o l / m^{3}$

$C_{A 2}^{*} = K^{2} C_{A 0}^{*} = 0.4144 m o l / m^{3}$

ここで

$K = \frac{F^{*}}{F * + V k} = 0.6693$

この例では、2 番目の反応器 $C_{A 2}^{*}$ からの排出反応物濃度が、供給濃度 $C_{A 0}$ に外乱がある場合でも維持されるようにコントローラーを設計します。操作変数は、最初の反応器に入る反応物のモル流量 F です。

線形プラントモデル

この制御設計例では、プラントモデルは次のようになります。

$\frac{C_{A 2} (s)}{F (s)}$

外乱モデルは次のようになります。

$\frac{C_{A 0} (s)}{C_{A 2} (s)}$

この化学プロセスは、次のブロック線図を使用して表すことができます。

ここで

$G_{A 1} = \frac{C_{A 1} (s)}{C_{A 0} (s)} = \frac{0.6693}{8.2677 s + 1}$

$G_{F 1} = \frac{C_{A 1} (s)}{F (s)} = \frac{2.4087}{8.2677 s + 1}$

$G_{A 2} = \frac{C_{A 2} (s)}{C_{A 1} (s)} = \frac{0.6693}{8.2677 s + 1}$

$G_{F 2} = \frac{C_{A 2} (s)}{F (s)} = \frac{1.6118}{8.2677 s + 1}$

ブロック線図に基づき、次のようなプラントモデルと外乱モデルを取得します。

$\frac{C_{A 2} (s)}{F (s)} = G_{F 1} G_{A 2} + G_{F 2} = \frac{13.3259 s + 3.2239}{(8.2677 s + 1)^{2}}$

$\frac{C_{A 2}}{C_{A 0}} = G_{A 1} G_{A 2} = \frac{0.4480}{(8.2677 s + 1)^{2}}$

コマンドラインでプラントモデルを作成します。

s = tf('s');
G1 = (13.3259*s+3.2239)/(8.2677*s+1)^2;
G2 = G1;
Gd = 0.4480/(8.2677*s+1)^2;

G1 はコントローラーの評価で使用される実際のプラントです。G2 は実際のプラントの近似で、IMC 構造内の予測モデルとして使用されます。G2 = G1 は、モデルの不一致が存在していないことを意味します。Gd は外乱モデルです。

制御システムデザイナーでの IMC 構造の定義

"制御システムデザイナー" を開きます。そうするには、MATLAB デスクトップの [アプリ] タブで [制御システムデザイナー] を選択します。あるいは、MATLAB コマンドプロンプトで「controlSystemDesigner」と入力します。

IMC 制御アーキテクチャを選択します。"制御システムデザイナー" で、[アーキテクチャの編集] をクリックします。[アーキテクチャの編集] ダイアログボックスで、[Configuration 5] を選択します。

システムデータを読み込みます。G1、G2、Gd について、モデルの [値] を指定します。

[OK] をクリックします。

補償器の調整

[アーキテクチャの編集] ダイアログボックスでプラントモデルおよび外乱モデルを指定すると、[制御システムデザイナー] で表示されているプロットが更新され、指定したモデルが反映されます。右下のプロットに、システムの閉ループステップ応答が表示されます。

プロットを右クリックし、[特性]、[立ち上がり時間] のサブメニューを選択します。立ち上がり時間マーカーにマウスを合わせます。

立ち上がり時間は約 25 秒です。IMC 補償器を調整して、閉ループ応答時間を速くします。

IMC 補償器を調整するには、"制御システムデザイナー" で [調整法] をクリックし、[内部モデルコントロール (IMC) の調整] を選択します。

[主要な閉ループの時定数] に 2 を選択し、[望ましいコントローラー次数] に 2 を選択します。

コントローラーを更新するには、[補償器の更新] をクリックします。

閉ループステップ応答プロットで、調整後のコントローラーによる閉ループの整定時間は約 4.4 秒です。

モデルが不一致の場合の性能の制御

コントローラーの設計においては、G1 が G2 と等しくなると仮定しました。実際には、これらは異なることが多く、設定値に追従して外乱を抑制するにはコントローラーが十分にロバストである必要があります。

G1 と G2 の間にモデルの不一致を発生させ、設定点の変化と負荷外乱の両方が存在する状態で、MATLAB® コマンドラインで制御性能を調べます。

IMC コントローラーを MATLAB ワークスペースにエクスポートします。[エクスポート] をクリックします。[モデルのエクスポート] ダイアログボックスで、補償器モデル C を選択します。

[エクスポート] をクリックします。

アプリで次のコントローラーがエクスポートされます。

C = zpk([-0.121 -0.121],[-0.2419, -0.5],2.5647)

C =
 
  2.5647 (s+0.121)^2
  ------------------
  (s+0.2419) (s+0.5)
 
Continuous-time zero/pole/gain model.

IMC 構造を、フィードフォワードパス内のコントローラーと単位フィードバックを備えた古典フィードバック制御構造に変換します。

C_new = feedback(C,G2,+1)

C_new =
 
               2.5647 (s+0.121)^4
  --------------------------------------------
  (s-0.0004396) (s+0.121) (s+0.1213) (s+0.242)
 
Continuous-time zero/pole/gain model.

次のプラントモデルを定義します。

モデルの不一致なし:

G1p = (13.3259*s+3.2239)/(8.2677*s+1)^2;

G1 の時定数を 5% 変更:

G1t = (13.3259*s+3.2239)/(8.7*s+1)^2;

G1 のゲインを 3 倍に増加:

G1g = 3*(13.3259*s+3.2239)/(8.2677*s+1)^2;

設定点の追従性能を評価します。

step(feedback(G1p*C_new,1),feedback(G1t*C_new,1),feedback(G1g*C_new,1))
legend('No  Mismatch','Mismatch in Time Constant','Mismatch in Gain')

外乱の抑制性能を評価します。

step(Gd*feedback(1,G1p*C_new),Gd*feedback(1,G1t*C_new),Gd*feedback(1,G1g*C_new))
legend('No Model Mismatch','Mismatch in Time Constant','Mismatch in Gain')