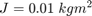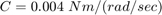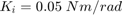ハードディスクの読み取り/書き込みヘッドコントローラーの設計

スクリプトを開く

この例では、古典制御設計法を使用して、コンピューターのハードディスクの読み取り/書き込みヘッド位置コントローラーを設計する方法を説明します。

読み取り/書き込みヘッドモデルの作成

ニュートンの法則に基づき、次の微分方程式を使用して読み取り/書き込みヘッドをモデル化します。

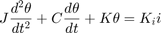
$J\frac{{{d^2}\theta }}{{d{t^2}}} + C\frac{{d\theta }}{{dt}} + K\theta = {K_i}i$

ここで

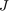はヘッドアセンブリの慣性です。
はベアリングの粘性減衰係数です。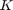
は戻しバネ定数です。
はモータートルク定数です。
$\theta$ はヘッドの角度位置です。
は入力電流です。

ラプラス変換を使用すると、から $\theta$ への伝達関数は次のようになります。

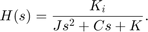
$H(s) = \frac{{{K_i}}}{{J{s^2} + Cs + K}}.$

次を満たすようなモデルの物理定数を指定します。

$J = 0.01\;kgm^2$
$C = 0.004\;Nm/(rad/sec)$
$K = 10\;Nm/rad$
$K_i = 0.05\;Nm/rad$

J = 0.01;
C = 0.004;
K = 10;
Ki = 0.05;

これらの定数を使用して伝達関数を定義します。

num = Ki;
den = [J C K];
H = tf(num,den)

H =
 
           0.05
  -----------------------
  0.01 s^2 + 0.004 s + 10
 
Continuous-time transfer function.

モデルの離散化

読み取り/書き込みヘッドの正確な位置決めを行うデジタルコントローラーを設計するには、まず連続時間プラントを離散化します。

サンプル時間を指定します。

Ts = 0.005;

モデルを離散化します。コントローラーはその入力に接続された (ゼロ次ホールドの) デジタルアナログコンバーターをもつので、c2d コマンドを使用して 'zoh' 離散化手法を指定します。

Hd = c2d(H,Ts,'zoh')

Hd =
 
  6.233e-05 z + 6.229e-05
  -----------------------
   z^2 - 1.973 z + 0.998
 
Sample time: 0.005 seconds
Discrete-time transfer function.

連続時間モデルと離散時間モデルのボード線図を比較します。

bodeplot(H,'-',Hd,'--')
legend('Continuous-time','Discrete-time')

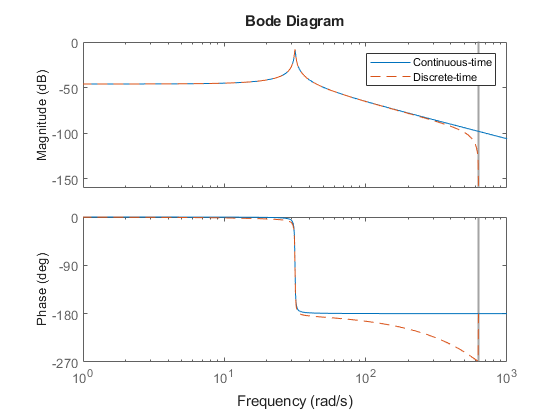
離散システムを解析するには、そのステップ応答をプロットします。

stepplot(Hd)

ステップ応答には大きな振幅があります。これはおそらく減衰が小さいためです。システムの開ループ極の減衰を確認します。

damp(Hd)

                                                                                    
         Pole             Magnitude     Damping       Frequency      Time Constant  
                                                    (rad/seconds)      (seconds)    
                                                                                    
  9.87e-01 + 1.57e-01i     9.99e-01     6.32e-03       3.16e+01         5.00e+00    
  9.87e-01 - 1.57e-01i     9.99e-01     6.32e-03       3.16e+01         5.00e+00

予想したとおり、極は小さな等価の減衰率をもち、単位円の近くにあります。したがって、システムの減衰を増加させる補償器を設計しなければなりません。

補償器のゲインの追加

最も簡単な補償器は、極や零点をもたないゲイン係数です。根軌跡法を使用して、適切なフィードバックゲインを選択してみてください。根軌跡は、閉ループ極の軌跡をフィードバックゲインの関数としてプロットします。

rlocus(Hd)

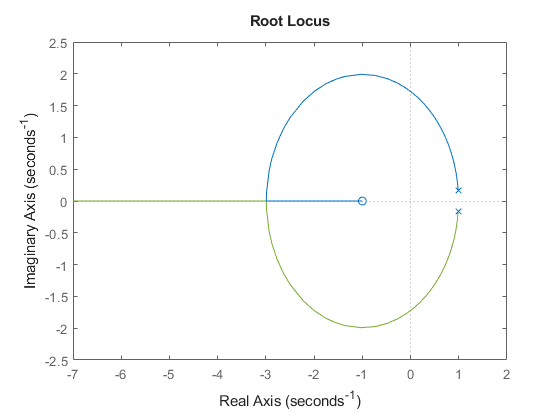
極は急激に単位円から離れて不安定になります。したがって、システムに進みを導入しなければなりません。

リードネットワークの追加

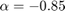$\alpha = -0.85$ に零点をもち、に極をもつ進み補償器を定義します。

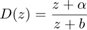
$D(z) = \frac{{z + \alpha }}{{z + b}}$

D = zpk(0.85,0,1,Ts);

対応する開ループモデルは、補償器とプラントの直列接続です。

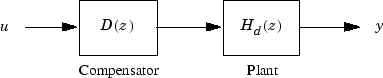
oloop = Hd*D

oloop =
 
  6.2328e-05 (z+0.9993) (z-0.85)
  ------------------------------
     z (z^2 - 1.973z + 0.998)
 
Sample time: 0.005 seconds
Discrete-time zero/pole/gain model.

進み補償器が開ループ周波数応答に与える影響を確認するには、Hd と oloop のボード線図を比較します。

bodeplot(Hd,'--',oloop,'-')
legend('Plant','Plant plus lead compensator')

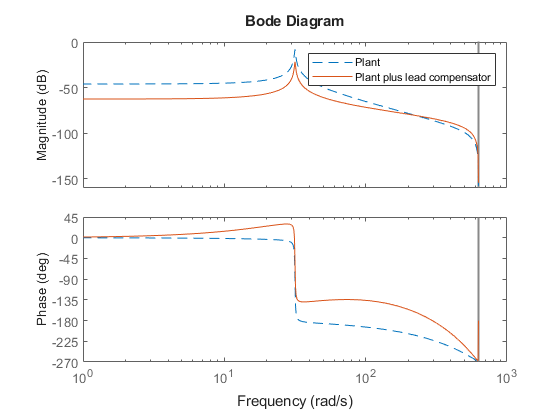
補償器がシステムに進みを追加し、それによって位相応答が周波数範囲 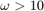$\omega > 10$ で上方向にシフトします。

根軌跡プロットを使用して、閉ループシステムの極の動作を調べます。x 軸と y 軸の両方の範囲を -1 ～ 1 に設定します。

rlocus(oloop)
zgrid
xlim([-1 1])
ylim([-1 1])

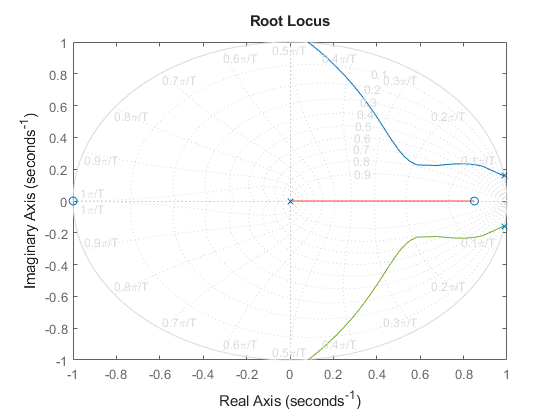
すると、閉ループ極はある程度の間、単位円内に留まります。

プロットのデータマーカーを作成するには、根軌跡の曲線をクリックします。マーカーをドラッグして、曲線上で減衰が最大になる点を見つけます。0.782 の最大減衰は、4.07e+03 のフィードバックゲインに対応します。

設計の解析

この設計を解析するには、まずフィードバックゲインが 4.07e+03 の開ループシステムで構成される閉ループシステムを定義します。

k = 4.07e+03;
cloop = feedback(oloop,k);

閉ループのステップ応答をプロットします。

stepplot(cloop)

この応答は、閉ループ設定点によって異なります。ここで示すものは、比較的速く、約 0.06 秒で落ち着きます。したがって、この閉ループディスクドライブシステムの探索時間は 0.06 秒です。今日の標準から見るとこの探索時間は比較的遅いものですが、ここでは若干減衰したシステムを使用しています。

設計のロバスト性を調査することを推奨します。これを行うには、システムのゲイン余裕と位相余裕を計算します。まず、補償器、プラント、フィードバックゲインを直列に接続して、単一フィードバックの開ループシステムを作成します。

olk = k*oloop;

次に、この開ループモデルの余裕を計算します。

[Gm,Pm,Wcg,Wcp] = margin(olk)

Gm =

    3.8360


Pm =

   43.3061


Wcg =

  296.7985


Wcp =

  105.4738

このコマンドはゲイン余裕 Gm、位相余裕 Pm、およびそのそれぞれの交差周波数 Wcg と Wcp を返します。

ゲイン余裕を dB に変換します。

20*log10(Gm)

ans =

   11.6776

余裕をグラフィカルに表示することもできます。

margin(olk)

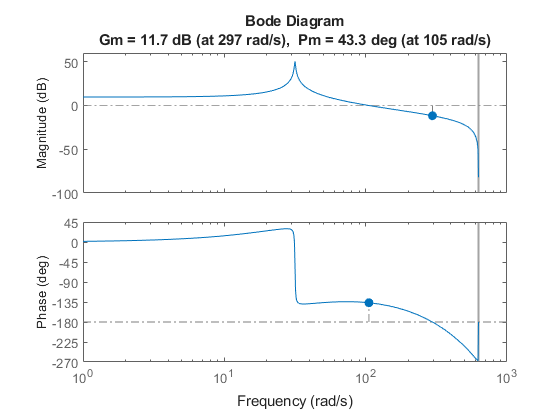
この設計はロバストであり、開ループシステムで 11 dB のゲインの増加または 40 度の位相遅れを不安定にならずに許容します。この設計の手順を続けることで、開ループシステムを安定化し、探索時間をさらに短縮する補償器を見つけられる場合があります。

参考

rlocus | bodeplot | feedback | margin

ハードディスクの読み取り/書き込みヘッド コントローラーの設計

読み取り/書き込みヘッド モデルの作成