ジェット旅客機のフォールトトレラント制御

この例では次を使用します。

この例では、プラントの複数の操作モードの固定構造コントローラーを調整する方法について説明します。

背景

この例では、ジェット旅客機の昇降舵および補助翼アクチュエータが停止した場合のフォールトトレラント飛行制御について説明します。飛行制御システムは、ノミナルな運航状況と、一部のアクチュエータがコントロールサーフェス損失により機能しなくなった劣化条件の両方において安定性を維持し、性能要件および快適性要件を満たさなければなりません。突風はすべての条件で軽減されなければなりません。この適用例は、極端な飛行条件下で航空機の安全性を維持しなければならないため "信頼制御" と呼ばれることがあります。

航空機モデル

制御システムは Simulink でモデル化されます。

addpath(fullfile(matlabroot,'examples','control','main')) % add example data
open_system('faultTolerantAircraft')

航空機は、次の状態変数 (速度の単位は mph、角速度の単位は deg/s) をもつ厳格な 6 次状態空間システムとしてモデル化されます。

u: x ボディ軸速度
w: z ボディ軸速度
q: ピッチレート
v: y ボディ軸速度
p: ロールレート
r: ヨーレート

状態ベクトルに加え、飛行経路のバンク角レート mu (deg/s)、迎角 alpha (deg) および横滑り角 beta (deg) も制御できます。制御入力は、右側の昇降舵、左側の昇降舵、右側の補助翼、左側の補助翼および方向舵の偏向角です。すべての偏向角は度数で表されます。昇降舵は対称的にグループ化されて迎角を生成します。補助翼は非対照的にグループ化されてロール運動を生成します。これにより、Simulink モデルに示される 3 つの制御動作が生じます。

コントローラーは、内側のループの状態フィードバック制御と外側のループの MIMO 積分動作で構成されます。ゲイン行列 Ki および Kx はそれぞれ 3 行 3 列と 3 行 6 列であるため、コントローラーには 27 個の調整可能なパラメーターがあります。

アクチュエータの故障

9 行 5 列の行列を使用してノミナルモードとさまざまなアクチュエータの故障モードを符号化します。各行は 1 つの飛行条件を表し、0 は対応する偏向表面の停止を示します。

OutageCases = [...
   1 1 1 1 1; ... % nominal operational mode
   0 1 1 1 1; ... % right elevator outage
   1 0 1 1 1; ... % left elevator outage
   1 1 0 1 1; ... % right aileron outage
   1 1 1 0 1; ... % left aileron outage
   1 0 0 1 1; ... % left elevator and right aileron outage
   0 1 0 1 1; ... % right elevator and right aileron outage
   0 1 1 0 1; ... % right elevator and left aileron outage
   1 0 1 0 1; ... % left elevator and left aileron outage
   ];

設計要件

コントローラーは次を行わなければなりません。

3 つの軸が適切に分離されたノミナル運航モードにおける、mu、alpha、beta による適切な追従性能の提供
10 mph の突風発生時の性能維持
アクチュエータ停止局面における安定性低下および性能低下の制限

最初の要件を表すには、統合された追従誤差 e と制御操作 u にペナルティを課す LQG に似たコスト関数を使用できます。

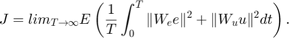
$J = lim_{T \rightarrow \infty} E \left( {1 \over T} \int_0^T \| W_e e \|^2 + \| W_u u \|^2 dt \right) .$

対角重み付け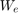および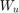は、応答性と制御操作をトレードし、一部のチャネルを他のチャネルよりも強調するための主要な調整ノブです。WeightedVariance 要件を使用してこのコスト関数を表し、停止シナリオでは性能の重み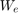を係数 2 で緩和します。

We = diag([10 20 15]);   Wu = eye(3);

% Nominal tracking requirement
SoftNom = TuningGoal.WeightedVariance('setpoint',{'e','u'}, blkdiag(We,Wu), []);
SoftNom.Models = 1;    % nominal model

% Tracking requirement for outage conditions
SoftOut = TuningGoal.WeightedVariance('setpoint',{'e','u'}, blkdiag(We/2,Wu), []);
SoftOut.Models = 2:9;  % outage scenarios

突風の緩和のため、突風モデルを駆動するホワイトノイズ wg による誤差信号 e の分散を制限します。停止シナリオの場合も、あまり厳密でない要件を使用します。

% Nominal gust alleviation requirement
HardNom = TuningGoal.Variance('wg','e',0.02);
HardNom.Models = 1;

% Gust alleviation requirement for outage conditions
HardOut = TuningGoal.Variance('wg','e',0.1);
HardOut.Models = 2:9;

ノミナル飛行でのコントローラーの調整

突風速度を 10 mph に設定し、コントローラーの調整可能な状態フィードバックゲインと積分器のゲインを初期化します。

GustSpeed = 10;
Ki = eye(3);
Kx = zeros(3,6);

slTuner インターフェイスを使用して調整タスクを設定します。調整対象のブロックをリストし、Simulink モデルで変数 outage を変化させて 9 つの飛行条件を指定します。slTuner ではスカラーパラメーターのみ変更できるため、outage ベクトルの各エントリの取る値を個別に指定します。

OutageData = struct(...
   'Name',{'outage(1)','outage(2)','outage(3)','outage(4)','outage(5)'},...
   'Value',mat2cell(OutageCases,9,[1 1 1 1 1]));
ST0 = slTuner('faultTolerantAircraft',{'Ki','Kx'},OutageData);

systune を使用して、ノミナル要件に従ってコントローラーゲインを調整します。突風の緩和を厳密な制約として扱います。

[ST,fSoft,gHard]  = systune(ST0,SoftNom,HardNom);

Final: Soft = 22.6, Hard = 0.99942, Iterations = 295

ゲイン値を取得し、飛行のノミナル条件と劣化条件に対する mu, alpha, beta でのステップコマンドへの応答をシミュレートします。すべてのシミュレーションには突風効果が含まれ、赤い曲線がノミナル応答です。

Ki = getBlockValue(ST, 'Ki');  Ki = Ki.d;
Kx = getBlockValue(ST, 'Kx');  Kx = Kx.d;

% Bank-angle setpoint simulation
plotResponses(OutageCases,1,0,0);

% Angle-of-attack setpoint simulation
plotResponses(OutageCases,0,1,0);

% Sideslip-angle setpoint simulation
plotResponses(OutageCases,0,0,1);

ノミナル応答は良好ですが、アクチュエータの停止が生じた場合の性能低下は許容されません。

障害の発生した飛行でのコントローラーの調整

信頼性を向上させるためには、ノミナルプラントのノミナル要件および 8 つのすべての停止シナリオの緩和要件に合わせてコントローラーゲインを再調整します。

[ST,fSoft,gHard]  = systune(ST0,[SoftNom;SoftOut],[HardNom;HardOut]);

Final: Soft = 25.7, Hard = 0.99987, Iterations = 548

最適性能 (LQG コスト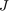の平方根) は、ノミナルな調整の場合よりも少しだけ低下しています (26 と 23)。ゲイン値を取得し、シミュレーションを再実行します (赤い曲線がノミナル応答)。

Ki = getBlockValue(ST, 'Ki');  Ki = Ki.d;
Kx = getBlockValue(ST, 'Kx');  Kx = Kx.d;

% Bank-angle setpoint simulation
plotResponses(OutageCases,1,0,0);

% Angle-of-attack setpoint simulation
plotResponses(OutageCases,0,1,0);

% Sideslip-angle setpoint simulation
plotResponses(OutageCases,0,0,1);

コントローラーは、この例で考慮されているすべての停止シナリオで許容される性能を提供します。アクチュエータのレート飽和を回避するための最小安定余裕やゲイン制限などの仕様を追加して、設計をさらに改善することができます。

rmpath(fullfile(matlabroot,'examples','control','main')) % remove example data

参考

systune (slTuner) (Simulink Control Design) | slTuner (Simulink Control Design) | TuningGoal.WeightedVariance | TuningGoal.Variance