離散時間モデルでのむだ時間の 1/z の因子への変換

この例では、離散時間モデルのむだ時間を 1/_z_ の因子に変換する方法を説明します。

離散時間モデルでは、1 サンプリング間隔のむだ時間はモデルの 1/_z_ (z = 0 の極) の因子と等価です。そのため、離散時間モデルの InputDelay、OutputDelay、または IODelay プロパティに格納されたむだ時間は、z = 0 で極として書き直すことによってモデルダイナミクスで書き直すことができます。ただし、追加の極はシステムの次数を増やします。特に、長いむだ時間では、これは非常に高次のシステムを生み出す可能性があり、長い計算時間や数値誤差を招きます。

離散時間閉ループモデルでむだ時間を無くす方法を示し、それを行う効果を確認するために、次の閉ループシステムを作成します。

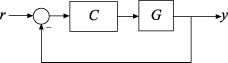
G は入力遅延のある 1 次離散時間システムであり、C は PI コントローラーです。

G = ss(0.9,0.125,0.08,0,'Ts',0.01,'InputDelay',7);
C = pid(6,90,0,0,'Ts',0.01);
T = feedback(C*G,1);

入力遅延のあるプラントでフィードバックループを閉じると、閉ループシステムで内部遅延が発生します。T の次数と内部遅延を調べます。

order(T)

ans = 2

T.InternalDelay

ans = 7

T は 2 次状態空間モデルです。1 つの状態は 1 次プラントが影響し、もう 1 つの状態は PI コントローラーの 1 つの極が影響します。遅延により、T の次数が増加することはありません。代わりに、7 つのタイムステップの内部遅延として表されます。

内部遅延を $z^{- 7}$ で置き換えます。

Tnd = absorbDelay(T);

このコマンドは、内部遅延を z = 0 において 7 つの極に変換します。これを確認するには、Tnd の次数と内部遅延を調べます。

order(Tnd)

ans = 9

Tnd.InternalDelay

ans =

  0x1 empty double column vector

Tnd には内部遅延はありませんが、7 単位遅延をモデルダイナミクスに吸収することによって導入された 7 つの余分な極のために、9 次モデルになります。

このような表現の違いはありますが、Tnd の応答は T の応答と厳密に一致します。

stepplot(T,Tnd,'r--')
legend('T','Tnd')

Figure contains an axes object. The axes object contains 2 objects of type line. These objects represent T, Tnd.

bodeplot(T,Tnd,'r--')
legend('T','Tnd')

Figure contains 2 axes objects. Axes object 1 contains 2 objects of type line. These objects represent T, Tnd. Axes object 2 contains 2 objects of type line. These objects represent T, Tnd.

参考

pade

離散時間モデルでのむだ時間の 1/z の因子への変換

参考

関連する例

詳細