HF 電離層チャネル モデル
この例では、Recommendation ITU-R F.1487 で説明されているモデルに基づいて高周波数 (HF) 電離層チャネルをシミュレートする方法を説明します。特に、一般的な Watterson チャネル モデルおよび HF モデムの定量試験で使用されるその他の簡略化されたチャネル モデルをシミュレートする方法を示します。Communications Toolbox™ のガウスおよび二重ガウスdoppler構造体と共にcomm.RayleighChannel System object™ と関数stdchanを使用します。
ITU-R HF チャネル モデル: 概要
HF 電離層無線通信では、送信される信号は電離層の E 層および F 層に何度も反射し、"モード" とも呼ばれる複数の伝播パスが生成されることがあります [1]。一般に、マルチパス遅延拡散はモバイル無線に比べて大きくなります。また、電離層の乱れのために信号がドップラー拡散の影響を受けることもあります。ただし、フェージング率は通常はモバイル無線の場合より小さくなります。
Recommendation ITU-R F.1487 [1] では、HF 電離層チャネルのシミュレーションに一般的なガウス分布モデルを使用することを推奨しています。このモデルは、Watterson のチャネル モデルに基づきます [2]。HF モデム試験では、パラメーターを指定したより簡単なモデルも [1] で推奨されています。
シミュレーション固有のパラメーターの初期化
このシミュレーションのサンプル レート Rs は 9.6K Hz に指定されており、この例の他の部分でも同じです。位相オフセットがゼロの QPSK 変調スキームを使用します。
Rs = 9.6e3; % Channel sampling rate M = 4; % Modulation order
Watterson チャネル モデル
Watterson チャネル モデルは、1 本のタップ付き遅延線で構成されます。各タップは分解可能な伝播パスに対応します。各タップに 2 つの磁気イオン成分が存在します。各成分は特定のゲインと周波数シフトをもつ複素ガウス ランダム過程としてモデル化され、そのドップラー スペクトルは特定の標準偏差をもつガウス分布です [2]。したがって、各タップの特徴は二重ガウス ドップラー スペクトルです。このスペクトルは周波数領域での 2 つのガウス関数で構成され、各関数には独自のパラメーター (電力ゲイン、周波数シフト、および標準偏差) のセットがあります。
この例では、[1] で示されている Watterson シミュレーション モデルを使用します。このモデルでは、2 つの磁気イオン成分に対応する、独立した 2 つの周波数シフト複素ガウス ランダム過程 (ガウス ドップラー スペクトルをもつ) を追加することで、各タップでの複素フェージング プロセスが得られます。このシミュレーション モデルにより、エンベロープが一般にはレイリー分布 "でない" 複素フェージング プロセスになります。したがって、シミュレーション モデルに忠実であるためには、二重ガウス ドップラー スペクトルをもつレイリー チャネルを単に作成するだけでは不十分です。代わりに、周波数シフトのガウス ドップラー スペクトルをもつ独立したレイリー チャネルを 2 つ作成し、それらをゲインスケーリングし、両方を合わせて二重ガウス ドップラー スペクトルをもつ Watterson チャネル モデルを得ます。単純にするため、タップが 1 つしかない Watterson チャネルをシミュレートします。
周波数シフトしたガウス ドップラー スペクトルは、ガウス関数が 1 つしか存在しない (2 番目のガウス関数の電力ゲインがゼロ) 二重ガウス ドップラー スペクトルと見なすことができます。したがって、各磁気イオン成分の周波数シフトしたガウス ドップラー スペクトルをエミュレートするため、2 つのガウス関数の一方に周波数シフトと標準偏差を指定し、もう一方のガウス関数の電力ゲインがゼロである二重ガウス ドップラー構造体を構築します。
最初の磁気イオン成分には、標準偏差 sGauss1、周波数シフト fGauss1、および電力ゲイン gGauss1 のガウス ドップラー スペクトルがあります。二重ガウス ドップラー構造体 dopplerComp1 は、2 番目のガウス関数の電力ゲインがゼロである (したがって、標準偏差と中心周波数は無関係であり、既定値になる) 一方、1 番目のガウス関数は正規化された標準偏差 sGauss1/fd と正規化周波数シフト fGauss1/fd をもつように構築します。ここで、正規化係数 fd は、対応するチャネルの最大ドップラー シフトです。この例では、2 番目のガウス関数のゲインがゼロなので、1 番目のガウス関数のゲインに割り当てられた値は無関係です (既定値 0.5 のままにします)。これは、後で作成するチャネル System object が割り当てられることで、このドップラー スペクトルのべき乗の合計が 1 になるように正規化されるからです。
二重ガウス ドップラー構造体の構築方法の詳細については、dopplerを参照してください。
fd = 10; % Chosen maximum Doppler shift for simulation sGauss1 = 2.0; fGauss1 = -5.0; dopplerComp1 = doppler('BiGaussian', ... NormalizedStandardDeviations=[sGauss1/fd 1/sqrt(2)], ... NormalizedCenterFrequencies=[fGauss1/fd 0], ... PowerGains=[0.5 0])
dopplerComp1 = struct with fields:
SpectrumType: 'BiGaussian'
NormalizedStandardDeviations: [0.2000 0.7071]
NormalizedCenterFrequencies: [-0.5000 0]
PowerGains: [0.5000 0]
磁気イオンの最初の成分をシミュレートするため、ドップラー構造体 dopplerComp1 によって指定される、周波数シフトしたガウス ドップラー スペクトルをもつ単一パスのレイリー チャネル System object chanComp1 を構築します。このチャネルの平均パス電力ゲインは 1 (0 dB) です。
chanComp1 = comm.RayleighChannel( ... SampleRate=Rs, ... MaximumDopplerShift=fd, ... DopplerSpectrum=dopplerComp1, ... RandomStream='mt19937ar with seed', ... Seed=99, ... PathGainsOutputPort=true)
chanComp1 =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 10
DopplerSpectrum: [1×1 struct]
ChannelFiltering: true
PathGainsOutputPort: true
Show all properties
同様に、2 番目の磁気イオン成分には、標準偏差 sGauss2、周波数シフト fGauss2、および電力ゲイン gGauss2 のガウス ドップラー スペクトルがあります。二重ガウス ドップラー構造体 dopplerComp2 は、2 番目のガウス関数の電力ゲインがゼロである (したがって、標準偏差と中心周波数は無関係であり、既定値になる) 一方、1 番目のガウス関数は正規化された標準偏差 sGauss2/fd と正規化周波数シフト fGauss2/fd をもつように構築します (この場合も、電力ゲインは無関係です)。
sGauss2 = 1.0; fGauss2 = 4.0; dopplerComp2 = doppler('BiGaussian', ... NormalizedStandardDeviations=[sGauss2/fd 1/sqrt(2)], ... NormalizedCenterFrequencies=[fGauss2/fd 0], ... PowerGains=[0.5 0])
dopplerComp2 = struct with fields:
SpectrumType: 'BiGaussian'
NormalizedStandardDeviations: [0.1000 0.7071]
NormalizedCenterFrequencies: [0.4000 0]
PowerGains: [0.5000 0]
磁気イオンの 2 番目の成分をシミュレートするため、ドップラー構造体 dopplerComp2 によって指定される、周波数シフトしたガウス ドップラー スペクトルをもつ単一パスのレイリー チャネル System object chanComp2 を構築します。
chanComp2 = comm.RayleighChannel( ... SampleRate=Rs, ... MaximumDopplerShift=fd, ... DopplerSpectrum=dopplerComp2, ... RandomStream='mt19937ar with seed', ... Seed=999, ... PathGainsOutputPort=true)
chanComp2 =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: 0
AveragePathGains: 0
NormalizePathGains: true
MaximumDopplerShift: 10
DopplerSpectrum: [1×1 struct]
ChannelFiltering: true
PathGainsOutputPort: true
Show all properties
次に示すループで、ある入力信号に対する Watterson チャネルへの出力を計算し、y に保存します。y を取得する際、chanComp1 の関数呼び出しにより最初の磁気イオン成分、chanComp2 の関数呼び出しにより 2 番目の成分の影響がエミュレートされます。
各磁気イオン成分の目的の電力ゲイン gGauss1 と gGauss2 を得るため、各磁気イオン成分の出力信号をそれに対応する振幅ゲイン sqrt(gGauss1) と sqrt(gGauss2) でスケーリングしなければなりません。
HF 環境で見られるドップラー シフトは低く、二重ガウス ドップラー スペクトルは 2 つのオブジェクトの組み合わせであることから、System object の組み込みの可視化を使用してドップラー スペクトルの測定値を得ることは適切ではありません。代わりに、チャネルの複素パス ゲインを保存しておき、後から各パスのドップラー スペクトルをコマンド ラインで計算することにします。次に示すループで、各磁気イオン成分に関連付けられる複素パス ゲインを対応する振幅ゲインでスケーリングした後に合計してチャネルの複素パス ゲインを取得し、g に保存します。
gGauss1 = 1.2; % Power gain of first component gGauss2 = 0.25; % Power gain of second component Ns = 2e6; % Total number of channel samples frmLen = 1e3; % Number of samples per frame numFrm = Ns/frmLen; % Number of frames [y, g] = deal(zeros(Ns, 1)); for frmIdx = 1:numFrm x = pskmod(randi([0 M-1],frmLen,1),M); [y1, g1] = chanComp1(x); [y2, g2] = chanComp2(x); y(frmLen*(frmIdx-1)+(1:frmLen)) = sqrt(gGauss1) * y1 ... + sqrt(gGauss2) * y2; g(frmLen*(frmIdx-1)+(1:frmLen)) = sqrt(gGauss1) * g1 ... + sqrt(gGauss2) * g2; end
ドップラー スペクトルは、複素パス ゲインから推定されてプロットされます。
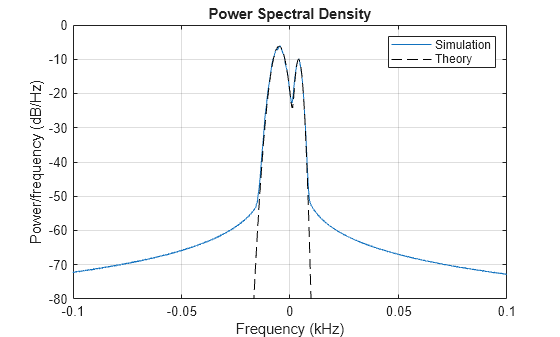
hFig = figure; pwelch(g, hamming(Ns/100), [], [], Rs, 'centered'); axis([-0.1 0.1 -80 0]); legend('Simulation');

推定されたドップラー スペクトルの上に理論的二重ガウス ドップラー スペクトルが重ね合わされます。両者はよく近似しています。
f = -(Rs/2):0.1:(Rs/2); Sd = gGauss1 * 1/sqrt(2*pi*sGauss1^2) ... * exp(-(f-fGauss1).^2/(2*sGauss1^2)) ... + gGauss2 * 1/sqrt(2*pi*sGauss2^2) ... * exp(-(f-fGauss2).^2/(2*sGauss2^2)); hold on; plot(f(Sd>0)/1e3,10*log10(Sd(Sd>0)),'k--'); legend('Simulation','Theory');
ITU-R F.1487 Low Latitudes, Moderate Conditions (LM) のチャネル モデル
Recommendation ITU-R F.1487 では、HF モデムの定量試験で使用される簡略化されたチャネル モデルを規定しています。これらのモデルは、電力の等しい 2 つの独立したフェージング パスで構成されます。各パスで、2 つの磁気イオン成分の周波数シフトはゼロであり分散は等しいと想定されます。したがって、各タップ上の二重ガウス ドップラー スペクトルは、単一のガウス ドップラー スペクトルに低減され、複素フェージング プロセスのエンベロープはレイリー分布になります。
次に、関数stdchanを使用して、ITU-R F.1487 の「Annex 3」で指定されている Low Latitudes, Moderate Conditions (LM) のチャネル モデルに従ってチャネル オブジェクトを構築します。パス遅延は 0 ms と 2 ms です。周波数拡散はガウス ドップラー スペクトルの標準偏差の 2 倍と定義されており、1.5 Hz です。したがって、ガウス ドップラー スペクトル構造体は、正規化された標準偏差 (1.5/2)/ fd で構築されます。ここで、fd は 1 Hz です (詳細を確認するには、help doppler と入力してください)。stdchanを使用して ITU-R HF チャネル モデルを構築するとき、最大ドップラー シフトを 1 Hz に設定しなければなりません。これにより、構築したチャネルのガウス ドップラー スペクトルの標準偏差は、確実に正しい値になります。
close(hFig); fd = 1; chanLM = stdchan('iturHFLM',Rs,fd); chanLM.RandomStream = 'mt19937ar with seed'; chanLM.Seed = 9999; chanLM.PathGainsOutputPort = true; chanLM.Visualization = 'Impulse response'
chanLM =
comm.RayleighChannel with properties:
SampleRate: 9600
PathDelays: [0 0.0020]
AveragePathGains: [0 0]
NormalizePathGains: true
MaximumDopplerShift: 1
DopplerSpectrum: [1×1 struct]
ChannelFiltering: true
PathGainsOutputPort: true
Show all properties
レイリー チャネル System object のインパルス応答の可視化は有効にされています。次に示すコードは LM チャネルをシミュレートし、その帯域制限インパルス応答を可視化します。既定では 4 サンプルごとに 1 つのチャネル応答を可視化してシミュレーションを高速化します。つまり、長さ 1000 のフレームの場合 1 番目、5 番目、9 番目、... 997 番目のサンプルの応答が表示されます。すべてのサンプルの応答を観察するには、chanLM の SamplesToDisplay プロパティを '100%' に設定します。
numFrm = 10; % Number of frames for frmIdx = 1:numFrm x = pskmod(randi([0 M-1],frmLen,1),M); chanLM(x); end

ここで、チャネル オブジェクトのドップラー スペクトルの可視化を有効化し、最初の離散パスの理論上のガウス ドップラー スペクトルと実測のガウス ドップラー スペクトルを観察します。ドップラー シフトが非常に低いため、実測スペクトルを理論上のスペクトルに収束させるには時間がかかることがあります。
release(chanLM); chanLM.Visualization = 'Doppler spectrum'; frmLen = 2e6; % Number of samples per frame numFrm = 80; % Number of frames for frmIdx = 1:numFrm x = pskmod(randi([0 M-1],frmLen,1),M); chanLM(x); end

参考文献
1 - Recommendation ITU-R F.1487, "Testing of HF modems with bandwidths of up to about 12 kHz using ionospheric channel simulators," 2000.
2 - C. C. Watterson, J. R. Juroshek, and W. D. Bensema, "Experimental confirmation of an HF channel model," IEEE® Trans.Commun.Technol., vol. COM-18, no. 6, Dec. 1970.